1 华南农业大学材料与能源学院 广州 510642;
2 华南农业大学公共基础课实验教学中心 广州 510642
2015-04-02 收稿, 2015-07-31 接受
基金项目: 2013年广东省高等学校教学质量与教学改革工程项目(粤教高函[2013]113-94)、2014年广东省本科高校教学质量与教学改革工程立项建设项目(粤教高函[2014]97号)和华南农业大学2013年度教育教学改革与研究重点项目(JG13012)资助
Explore on Data Processing in Fundamental Chemistry Experiment with Introducing Uncertainty
1 College of Materials and Energy, South China Agricultural University, Guangzhou 510642;
2 Center of Experimental Teaching for Basic Courses, South China Agricultural University, Guangzhou 510642
基础化学实验是一门重要的基础课,无论是化学化工相关专业,还是环境、生物、医学、农学等专业都需要开设,这些专业的学生都应该进行必要的化学实验技能训练。实验数据处理是基础化学实验课程中不可回避的问题,数据处理能力被看作学生科学素养的重要组成部分。
1993年由国际计量局(BIPM)、国际电工委员会(IEC)、国际临床化学联合会(IFCC)、国际标准化组织( ISO)、国际纯粹与应用化学联合会(IUPAC)、国际理论与应用物理联合会(IUPAP)、国际法定计量组织(OIML) 联合发布了《测量不确定度表示指南(GUM)》。1995年经修订版GUM公布于世,得到普遍认可,并得到了日益广泛的应用[1~3]。我国实施与国际接轨的测量不确定度评定以及测量结果包括其不确定度的表示方法,是不同学科之间交流的需要,也是适应全球市场经济发展的需要。无论是从培养人才的角度还是实验数据处理的实际需求,不确定度的学习和应用都是必要的。不确定度概念在大学物理教学和物理实验教学中有所讨论[4~6],但目前出版的基础化学实验教材和基础化学实验教学研究中鲜见涉及。引入不确定度表示测量结果是一项重大的课程内容改革,需要慎重行事,深入探讨。
目前基础化学实验数据处理方法教学的主线是:以误差理论为基础,分析误差的来源及校正方法;分析准确度与精密度的关系;用置信区间表示实验结果。根据当前误差理论和不确定度研究进展及其推广应用的情况,基础化学实验数据处理方法显示出一定的局限性:(1) 在系统误差得到校正的情况下,可以用置信区间表示测定结果,但实验过程中的误差主要来自系统误差,而且就基础化学实验中使用的方法和实验条件而言并未得到校正,以多次重复测定的标准偏差为基础的置信区间并未抓住主要矛盾;(2) 在介绍准确度与精密关系时特别强调“准确度高要求精密度要高,精密度高不一定准确度高”,而标准偏差或置信区间仅仅从精密度的角度对结果进行评定,即对实验准确度只能证伪,不能证真。
国家质量监督检验检疫总局组织制订了《测定不确定度评定与表示》(JJF1059-1999),并于2012进行了修订(JJF1059.1-2012),不确定度逐步成为一个应用于科学、技术、商业、工业、卫生、安全和管理等领域的概念。不确定度的相关标准试图分析所有的不确定性,并要求分析其相关性及合成,处理过程繁琐,还有许多经验因素,这也成为其致命弱点。由于不确定度处理的复杂性,部分专业人士都有畏难情绪,因此不同行业制订了操作性强一些的规范[7]。
按照JJF1135-2005《化学分析测量不确定度评定》[8]或JJF1059.1-2012《测量不确定度评定与表示》[9]规定的程序处理实验数据,考虑的因素多,程序复杂,标准中的实例亦受到诸多质疑[10]。因此,该标准中的处理程序在基础化学实验中几乎不具有可操作性。考虑到基础化学实验是非专业领域的实验,实施者也非专业人士,制订带有普遍意义并操作性强的规范难度很大。即使有操作规范,也会增加学生不必要的负担。因此,本文结合教学实际,探讨理解误差和不确定度概念与处理基础化学实验数据相结合的简化方案。
误差的定义为测量值与真值之差。误差可正可负,可以计算单个测量值的误差,也可计算多次测定结果平均值的误差。真值通常是接受参照值,来自于科学原理的理论值或确定值,一些国家或国际组织的实验工作的指定值或认证值,基于科学或工程组织赞助下合作实验工作中的同意值或认证值。
与生产实际中的测试不同,基础化学实验主要目的是为了练习操作和验证现有理论,有相当多的情况是能得到真值的,如摩尔质量、离解常数等某些常数的测定,用纯样品配制的供试样品测定或用已知样品对实验方法的验证等。
例如,用排水集气法测定镁的摩尔质量[11],3次平行测定。3次测定结果及其平均值均可根据误差的定义直接计算误差。主要影响因素包括镁条的质量、氢气体积、温度及压强等,可根据实验中选用的测量仪器和方法分析误差的主要来源,确定主要影响因素,明确对结果影响最大的操作和注意事项。镁条的质量用分析天平称量,最大允许误差为±0.0001g,镁条的质量为0.03××g,按0.03g计,相对误差最大值为±0.33%;用量气管量取氢气的体积,最大允许误差为±0.02mL,按30mL计,相对误差最大值为±0.07%;用室温近似代替量气管内氢气温度,室温与管内气体温度的差异若以最大±1℃计算,按温度298K计,相对误差最大值为±0.33%;用室内大气压代替管内气体压强,若管内外液面相差最大为1cm,即产生±1cm水柱的压强误差,按101.325kPa计,产生的最大相对误差为±0.10%。由以上分析可知,实验误差主要来自镁条的质量和管内气体的温度。由于镁条称样量较少,本实验中称量带来的相对误差较大,在实验中要特别注意分析天平的校准和正确操作。若镁条表面氧化层未除尽,则产生更大误差。另外,量气管内气体直接与水接触,容易造成量气筒内气体与室内空气的温度差别,很容易造成1~2℃差别,所以要尽量使量气管内气体温度与室温接近,并在确定接近平衡时及时读取室温。可以在产生氢气的反应完成后静置一段时间,并且千万不能用手直接抓住量气管。
在此先引用几个计算不确定度的实例。由于篇幅限制,不列举详细计算过程。
例1:ICP-AES测定沘江流域农田土壤中重金属元素Pb的不确定度[12]。结果如表 1。
表 1
Table 1
表 1(Table 1)
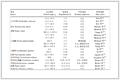
表 1 ICP-AES测定Pb的不确定度分量[12]
Table 1 Uncertainty components of Pb determination with ICP-AES
|
不确定度来源 |
相对标准不确定度/% |
|
校准曲线 |
1.41 |
|
称样 |
0.12 |
|
样品定容体积 |
0.078 |
|
测量重复性 |
0.223 |
|
称液管 |
0.20 |
|
容量瓶 |
0.052 |
|
贮备液 |
0.70 |
|
仪器稳定性 |
2.83 |
|
合成 |
3.25 |
|
表 1 ICP-AES测定Pb的不确定度分量[12]
Table 1 Uncertainty components of Pb determination with ICP-AES
|
在ICP-AES法测定Pb的实验中,相对标准不确定度的主要分量为校准曲线(1.41%) 和仪器稳定性(2.83%),其他不确定度分量可以忽略不计。这是一个典型的仪器分析实验,其不确定度的主要来源与大多数仪器分析实验相似。因此,在仪器分析中主要考虑仪器的稳定性。
例2:用HCl标准溶液测定样品中KOH的质量分数[9]。结果如表 2。
表 2
Table 2
表 2(Table 2)

表 2 用HCl标准溶液测定KOH的不确定度分量[9]
Table 2 Uncertainty components of KOH determination with HCl standard solution
|
不确定度来源 |
相对标准不确定度/% |
|
消耗标准溶液的体积 |
0.35 |
|
盐酸标准溶液浓度 |
0.05 |
|
KOH的相对分子质量 |
0.0053 |
|
样品质量测定 |
0.01 |
|
合成 |
0.35 |
|
表 2 用HCl标准溶液测定KOH的不确定度分量[9]
Table 2 Uncertainty components of KOH determination with HCl standard solution
|
在HCl标准溶液测定样品中KOH的质量分数实验中,相对标准不确定度主要分量为消耗标准溶液的体积(0.35%),其他不确定度分量可以忽略不计。这与大部分滴定分析的情况一致,滴定管测量的体积是主要的误差来源。在滴定时尽量选用A级滴定管,规范滴定操作。
例3:重量法测定石膏中三氧化硫[13]。结果如表 3。
表 3
Table 3
表 3(Table 3)

表 3 重量法测定石膏中SO3的不确定度分量[13]
Table 3 Uncertainty components of determination of SO3 in plaster with gravimetric method
|
不确定度来源 |
相对标准不确定度/% |
|
试料的质量 |
0.20 |
|
燃烧后的质量 |
0.48 |
|
硫酸钡摩尔质量 |
0.0027 |
|
三氧化硫摩尔质量 |
0.0059 |
|
测量重复性 |
0.0063 |
|
合成 |
0.52 |
|
表 3 重量法测定石膏中SO3的不确定度分量[13]
Table 3 Uncertainty components of determination of SO3 in plaster with gravimetric method
|
在重量法测定石膏中SO3的含量实验中,相对标准不确定度主要分量为试料的质量(0.20%) 和燃烧后的质量(0.48%),即误差来源主要是恒重过程,这符合绝大部分重量法分析的情况。
从以上3个实例可以看出,实验中的不确定度分量只有1~2个是主要分量,其他均可忽略。例1中,由校准曲线(1.41%) 和仪器稳定性(2.83%) 不确定度分量合成的不确定度为3.16%,与总合成不确定度3.25%相比,忽略其他因素产生的相对误差为2.8%;例2中,消耗标准溶液的体积不确定度分量(0.35%) 与总合成不确定度相比,忽略其他因素产生的误差为0;例3中,试料的质量(0.20%) 和燃烧后的质量(0.48%) 不确定度分量合成的不确定度为0.52%,与总合成不确定度0.52%相比,忽略其他因素产生的相对误差为0。
实际上,只要次要不确定度分量与主要不确定度分量之比在0.3以下,计算总合成不确定度时忽略其他不确定度分量所产生的相对误差即可控制在5%以内。估算如下:若以主要不确定度分量为1计,次要不确定度分量为0.3计,合成不确定度为1.04,仅考虑主要不确定度分量产生的相对误差为4%。因此,仅考虑主要不确定度分量是可行的。可以通过估算1~2个最大的不确定度分量合成总不确定度。
不确定度评估已在校准和实验室认可中执行,在各行业中的推广应用也日益广泛,不确定度的概念及其基本计算方法应成为许多专业大学生必需掌握的内容。
在基础化学实验中,通常没有仪器和标准样品(溶液) 的检定证书,完整计算不确定度困难较大. 通过误差分析,在帮助学生掌握误差概念的同时,可以查找实验误差的主要来源;通过误差的主要来源可以查明不确定度的主要分量,根据1~2个主要不确定度分量即可计算总不确定度。不确定度计算可以让学生进一步理解误差概念,并在一定的近似条件下完成不确定度计算,对数据处理过程不会产生畏难情绪。通过基础化学实验中的训练,已具备一定的不确定度计算的理论基础和操作经验,为根据不同行业规范完成不确定度计算打下良好基础。
 2016,
Vol. 79
2016,
Vol. 79 Issue (1): 92-95
Issue (1): 92-95 2016,
Vol. 79
2016,
Vol. 79 Issue (1): 92-95
Issue (1): 92-95