昌吉学院化学与应用化学系 新疆 昌吉 831100
基金项目:新疆昌吉学院博士启动基金项目(2014BSQD001)
Department of Chemistry and Applied Chemistry, Changji College, Changji 831100, China
闪蒸是连续的单级蒸馏过程,该过程主要用于化工过程混合物的初步分离。闪蒸罐是单级平衡蒸馏单元,是多级分离塔的基本构成单元,其模拟方法是复杂多级分离模拟化和模拟计算的基础,对于沸程较宽的多组分混合物的粗分离应用更多。本文系统地讨论了利用Excel解决理想溶液或接近理想溶液5种常见工况的具体解题过程。
1 闪蒸过程介绍
多组分物料典型的闪蒸过程如图 1所示。进料摩尔流率为 F ,组成为 z i,通过闪蒸罐进行部分气化和部分冷凝,在温度 t 、压力 p 下分离成气、液两相。气相流率为 V ,组成为 y i;液相流率为 L ,组成为 x i。
2 理论模型
闪蒸计算涉及质量衡算、热量衡算和相平衡关系[1]。对于任意组分 i 的质量衡算式为:
|
${{x}_{i}}L+{{y}_{i}}V={{Z}_{i}}F$
|
(1)
|
总质量衡算式为:
产品中任一组分的平衡关系为:
|
${{y}_{i}}={{k}_{i}}{{x}_{i}}~$
|
(3)
|
把式(2) 中的F和式(3) 中的 yi 分别代入式(1) ,可得:
|
${{x}_{i}}={{z}_{i}}~\frac{1+\text{ }\frac{V}{L}}{1+\text{ }\frac{{{K}_{i}}V}{L}\text{ }}$
|
(4a)
|
把式(1) 中的 L 和 yi 分别用式(2) 和式(3) 表示,可得:
|
${{x}_{i}}=\text{ }\frac{{{z}_{i}}}{({{K}_{i}}-1)\text{ }\left( V/F \right)+1}~$
|
(4b)
|
把式(1) 中的 F 和 xi 分别用式(2) 和式(3) 表示,可得:
|
${{y}_{i}}=\text{ }\frac{{{z}_{i}}\left( 1+\text{ }\frac{V}{L}\text{ } \right)\text{ }}{1+\text{ }\frac{{{K}_{i}}V}{L}}$
|
(5)
|
把式(4) 等号两边同乘以 L ,可得组分 i 的液相流率 li 为:
|
${{l}_{i}}=\text{ }\frac{{{f}_{i}}}{1+\text{ }\frac{{{K}_{i}}V}{L}}~$
|
(6)
|
把式(5) 等号两边同乘以 V ,可得组分 i 的气相流率 vi 为:
|
${{v}_{i}}=\frac{\text{ }{{f}_{i}}~}{1+\text{ }\frac{{{K}_{i}}V}{L}}$
|
(7)
|
组分 i 和 j 的 f / v 分别用式(7) 表示,得:
|
$\frac{{{f}_{i}}~}{{{v}_{i}}}~=1+\text{ }\frac{{{K}_{i}}V}{L}$
|
(7a)
|
|
$\text{ }\frac{{{f}_{j}}}{{{v}_{j}}}~~=1+\text{ }\frac{{{K}_{j}}V}{L}$
|
(7b)
|
把式(7a)和式(7b)等式两边同减1后相除,化简可得:
|
$\frac{{{f}_{i}}~}{{{v}_{i}}}~={{\alpha }_{ij}}(\text{ }\frac{{{f}_{i}}~}{{{v}_{i}}}~-1)\text{ }+1$
|
(8)
|
其中:
|
${{\alpha }_{ij}}=\text{ }\frac{{{K}_{i}}~}{{{K}_{j}}}$
|
(9)
|
对于理想溶液或接近理想溶液,组分 i 的平衡常数 Ki 的计算式为:
|
${{K}_{i}}=\text{ }\frac{{{p}_{i}}{{~}^{0}}}{p}$
|
(10)
|
其中: pi 0 是组分 i 的饱和蒸气压,通过Antonine公式求解。Antonine系数来自文献[1]。
归一方程为:
|
$\sum {{y}_{i}}-\sum {{x}_{i}}=0$
|
(11)
|
3 “单变量求解”功能简介
利用Excel软件计算多组分闪蒸问题,如手工计算,工作量大;对于一些工况可能涉及试差计算,手工解决不了[2-7]。具体体现在由公式(10) 计算不同组分的平衡常数 Ki 时,因为 Ki 是闪蒸温度和压力的函数,当闪蒸的温度或压力未知时,涉及试差计算。
“单变量求解”位于Excel软件“数据”菜单中的“模拟分析”中。可以解决使目标函数达到目标值时因变量的取值问题。当启用“单变量求解”时,通过不断改变可变单元格中的值,直到目标单元格的公式返回所需的目标值为止。利用Excel的单变量求解功能求解化工问题多有文献报道[8-10],本文利用Excel“单变量求解”功能解决闪蒸问题中当闪蒸温度或压力未知时试差过程。
4 闪蒸过程操作型计算的5种工况
闪蒸分离烃类混合物,原料含有物质的量的分数为分别为20 %、50% 和30%的正丁烷、正戊烷和正己烷,以200 mol/h的进料速率进行连续、稳定的闪蒸。根据不同的工艺条件,分为5种计算类型[1]:(1) 工况1:已知闪蒸温度 t 和关键组分 i 的气化率 vi / fi ,求解蒸气的流量和组成以及所需的压力。(2) 工况2:已知闪蒸压力 p 和闪蒸温度 t ,求解产品气液相的组成 xi 、 yi 。(3) 工况3:已知闪蒸压力 p 和总气化率 V / F ,求解闪蒸温度 t 和产品气液相的组成 xi 、 yi 。(4) 工况4:已知闪蒸压力 p 和某个组分的气化率 vi / fi ,求解闪蒸温度 t 和产品气液相的组成 xi 、 yi 。(5) 工况5:已知闪蒸压力 p 和产品的热焓,求解闪蒸温度 t 和和产品气液相的流率 vi 、 li 。具体的计算工况如下。
4.1 工况1
在121 ℃时达到产品平衡。在液体中回收90%己烷。计算蒸气的流量和组成以及所需的压力。具体的计算过程和结果见表 1。
表 1
Table 1
表 1(Table 1)
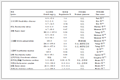
表 1 工况1的计算结果
Table 1 Calculating result of the first case
|
表 1 工况1的计算结果
Table 1 Calculating result of the first case
|
由于 Ki = f ( t ,p ),当闪蒸压力未知,存在试差计算问题。试差的具体过程:(1) 首先假设闪蒸压力 p ,根据已知的温度 t 由Antonine公式计算各组分的 pi 0 。再由假设的压力 p 根据公式(10) 计算出各组分 i 的平衡常数 Ki 。(2) 由公式(9) 分别计算丁烷与戊烷对己烷的相对挥发度 αj 已烷。(3) 根据关键组分己烷的 f 己烷/ v 己烷,由公式(8) 计算丁烷和戊烷的 f 丁烷/ v 丁烷和 f 戊烷/ v 戊烷。(4) 根据各组分的 fi 和 fi / vi ,计算 vi 。(5) 计算总的气相流率 V = v1+ v2+ v3,总的液相流率 L = F - V 。(6) 由公式 yi = vi / V ; xi =( fi - vi )/ L 计算各组分的气相摩尔分率 yi 和液相摩尔分率 xi 。(7) 计算闪蒸压力 p = p 假设( K1 x1 + K2 x2 + K3 x3) 。判断计算的闪蒸压力 p 与假设的闪蒸压力 p 是否相同。如果相同,假设正确,如果不同,重新假设闪蒸压力 p 。这个试差过程可借助Excel中的“单变量求解”功能实现,避免试差计算。
利用Excel计算此工况的具体过程如下。首先根据已知条件在单元格B9中输入公式“=1/(1-B7) ”,计算关键组分己烷的 f 己烷/ v 己烷。然后,开始试差计算闪蒸压力。假设初始值 p 0=10 atm于B10。在B12、B13、B14中依次计算进料各组分的摩尔流率 fi (首先在单元格B12中输入“=B2*B5”,利用“填充柄”功能快速计算出B13和B14中的数值)。由公式(10) 在B12、B13、B14中计算出 K 丁烷、 K 戊烷、 K 己烷。在单元格D12、D13、D14中计算 αj 已烷(如在D12中输入“=C12/C14”)。在E12、E13、E14中计算 fj / vj (如E12中输入“=($\$$B$\$$9-1) /D12+1”)。在F12、F13、F14中算出 vj (如F12中输入“=B12/E12”)。利用工具栏中的“自动求和”算出 V (如F15中输入“=SUM(F12:F14) ”)。在单元格F16中输入“=B5-F15”算出 L 。在G12、G13、G14中计算 yi 。(如G12中输入“=F12/$\$$F$\$$15”)。在H12、H13、H14中输入公式( fj - vj )/ L (如H12中输入“=(B12-F12) /$\$$F$\$$16”计算 xj 。在B17中输入“=B10*(C12*H12+C13*H13+C14*H14) ”重新计算出总压 p 。最后,在B18中输入“=B10-B17”算出假设的 p 与计算的 p 的差值f( x )。因为,f( x )≠0,启动“单变量求解”,以B18为目标单元格,目标值=0,B10为可变单元格,如图 2,点击“确定”后,计算出闪蒸压力为9.291 atm。
4.2 工况2
在压力10 atm和温度132.22 ℃时达到产品平衡。试计算产品中气、液的流量和组成。
已知操作 p 和 t 。首先需要判定闪蒸之后系统是否处于两相区内。即满足 V / F =0,f( V / F )>0; V / F =1,f( V / F )<0。其中f( V / F )为式(12) 。
检验函数为:
|
$\frac{V}{F}=\sum \frac{{{z}_{i}}({{K}_{i}}-1)}{({{K}_{i}}-1)\text{ }\left( V/F \right)+1}=0$
|
(12)
|
工况2的具体计算过程如表 2所示。首先核算是否存在2个相。计算 V / F =0时f( V / F )的值(如表 2中单元格F15所示0.226) ,其中,在E12中输入“=(B12-1) *$\$$F$\$$10+1”,在F12中输入“=D12/E12”,在F15中输入“=SUM(F12:F14) ”。计算 V / F =1时f( V / F )的值(如表 2中单元格H15所示-0.105) 。当确定平衡时,气液共存,可假设 V / F =0.5时,重新计算f( V / F )的值(如单元格F23所示,输入的公式为“=SUM(F20:F22) ”)。因为,f(V/F)≠0,启动“单变量求解”,以F23为目标单元格,目标值=0,F18为可变单元格。“确定”后,Excel计算出 V / F 为0.649。最后,由公式(4) 在单元格G20、G21、G22计算出 xi (如G20中输入“=C20/((B20-1) *$\$$F$\$$18+1) ”)。由公式(3) 在单元格H20、H21、H22计算 yi (如H20中输入“=G20*B20”)。根据已知的 F 和计算出的 V / F 的值,在单元格B24中输入“=F18*B5”计算出 V ,在单元格B25中输入“=B5-B24”计算出 L 。计算结果见表 2。
表 2
Table 2
表 2(Table 2)

表 2 工况2的计算结果
Table 2 Calculating result of the second case
|
表 2 工况2的计算结果
Table 2 Calculating result of the second case
|
4.3 工况3
在压力10 atm和气化率0.6时达到产品平衡。试计算产品温度和气液组成。
指定 p 和 V / F 。此时,因 t 未知,Ki未知,所以,首先假设一个 t 值,按工况2的具体计算过程由公式(12) 计算出f (t )的值(即工况2中f( V / F )的值),只是此时式(12) 是 t 的函数。重复这一过程,直至假设的 t 满足f( t )=0。值得注意:温度的初值取值区间为[泡点,露点]。
工况3的具体计算过程如表 3所示。在F9中假设 t 值(如100 ℃),首先计算出f( t )的值于单元格F14,其中,单元格E11中输入“=(B11-1) *$\$$B$\$$6+1”,单元格F11中输入“=D11/E11”,单元格F14中输入“=SUM(F11:F13) ”。因为,f( t )≠0,启动“单变量求解”,以F14为目标单元格,目标值为0,F9为可变单元格。“确定”后,Excel计算出t为131.461 ℃。最后,根据公式(4) 和公式(3) 分别在单元格G11、G12、G13和H11、H12、H13计算出 xi 和 yi (如G11中输入“=C11/E11) ”,H11中输入“=G11*B11”)。计算结果如表 3所示。
表 3
Table 3
表 3(Table 3)

表 3 工况3的计算结果
Table 3 Calculating result of the third case
|
表 3 工况3的计算结果
Table 3 Calculating result of the third case
|
4.4 工况4
在压力10 atm达到产品平衡。戊烷的气化分率为0.55,试计算产品温度和气液组成。
指定 p 和某个组分的气化率 v r/ f r。此时,具体计算过程可按照如下过程:可先假定 t ,然后按照工况1的具体计算过程求解出其他组分的 vi / fi ,将 vi 相加得 V 。由 V / F 和指定组分的 v r/ f r求得 K r,因 K r仅仅是 t 的函数,所以可将 K r转变为 t 。如假设的 t 与计算出的 t 相等,则停止计算,否则重新假设 t 。
工况4的具体计算过程如表 4所示。在B9中假设 t 值(如100 ℃),按工况1的具体计算过程计算 vj、V、L、yj 和 xj 。然后,在单元格B15中输入“=G12/H12”,计算出 K 戊烷,最后,计算在假设的温度下计算的 K 戊烷与最后算出的 K 戊烷的差值f( x )。因为,f( x )≠0,启动“单变量求解”,以B15为目标单元格,目标值=0,B9为可变单元格。“确定”后,EXCEL计算出闪蒸温度为130.340 ℃。计算结果如表 4所示。
表 4
Table 4
表 4(Table 4)

表 4 工况4的计算结果
Table 4 Calculating result of the fourth case
|
表 4 工况4的计算结果
Table 4 Calculating result of the fourth case
|
4.5 工况5
有100 mol/h的泡点料液,其温度为150 ℃,总压为10 atm,组成为物质的量分数分别为30%、40%和30%的正丁烷、正戊烷和正己烷。混合液经过绝热节流至7.0 atm而得到平衡的气液产品。试求产品温度和气液中各组分的流量。
指定 p 和产品的热焓,即料液通过节流膨胀达到闪蒸。显然,此种工况的计算较之前面4种工况计算过程复杂。首先假定一个居中的参考组分的 v r/ f r。所有其他组分的 vi / fi 值由 v r/ f r按式(8) 计算。然后将 vi 相加得 V 。由 V / F 和 v r/ f r求 K r,K r仅仅是 t 的函数,则可由 K r求出 t 。这一 t 值是单独由平衡条件确定的,可以独立地用总热量衡算来验算。然后进行迭代计算,直至温度和热焓衡算收敛为止。
表 5
Table 5
表 5(Table 5)

表 5 热焓与温度的关系
Table 5 Relation of enthalpy and temperature
| 组分 | 热焓/(kJ/kg)与温度/℃的关系 |
| 正丁烷 | 液体 | h=0.0049 t2 +2.121 t+281.61 R2=0.9997
H =0.0045 t2 +1.3573 t +661 R2=0.9997 |
| 蒸气 |
| 正戊烷 | 液体 | h=0.0041 t2 +2.1167 t +263.67 R2=0.9996
H=0.0037 t2 +1.42 t +654.49 R2=0.999 |
| 蒸气 |
| 正己烷 | 液体 | h=0.0013 t2 +2.3579 t +250.25 R2 = 0.9995
H= 0.0041 t2 +1.3133 t+638.97 R2=0.9986 |
| 蒸气 |
|
表 5 热焓与温度的关系
Table 5 Relation of enthalpy and temperature
|
表 6
Table 6
表 6(Table 6)

表 6 平衡常数Ki与温度t的关系
Table 6 Relation of equilibrium constant and temperature
| 组分 | 平衡常数K与温度/℃的关系 |
| 正丁烷 | K = 0.0002 t2 -0.0125 t+0.4431 R2=0.9999 |
| 正戊烷 | K = 0.0002 t2 -0.0201 t+0.5720 R2=0.9988 |
| 正己烷 | K = 2E-07 t3+2E-05 t2 -0.0022 t+0.0613R2=0.9999 |
|
表 6 平衡常数Ki与温度t的关系
Table 6 Relation of equilibrium constant and temperature
|
在开始计算前,先要找出正丁烷、正戊烷、正己烷的热焓与温度的关系,平衡常数与温度的关系。据参考文献[1],可以得出热焓与温度的关系见表 5,平衡常数与温度的关系见表 6。
工况5的具体计算过程如表 7所示。在B10中假设 v 戊烷/ f 戊烷值(如0.5) ,在B11中假设 t 平衡(如100 ℃)。根据前面拟合出的热焓(kJ/kg)与温度(℃)的关系计算出料液的热焓(如单元格E17所示)。根据假设的 v 戊烷/ f 戊烷值和假设 t 平衡,按工况4的具体计算过程于单元格B24中计算出 K 戊烷,并把它换算为10 atm下的 K 戊烷(如B26中输入“=B24*7/10”)。并由10 atm下的 K 戊烷求出对应的 t 于单元格B27中。在单元格B28中算出估计 t 的差值。在新算出的 t 下,根据拟合的热焓与温度的关系在单元格B35中计算出产品的热焓(如B35中输入“=G34+H34”)。最后,在单元格B36计算出产品的热焓与料液的热焓的差值(如B36中输入“=B35-E17”)。因为,t - t 平衡估(如单元格B28所示)≠0,H 产品- H 料液(如单元格B36所示)≠0,所以,首先启动“单变量求解”,以B28为目标单元格,目标值=0,B11为可变单元格。“确定”后,Excel重新计算。然后再启动“单变量求解”,以B36为目标单元格,目标值=0,B10为可变单元格。“确定”后,Excel重新计算。如此反复交替使用“单变量求解”使得 t - t平衡估=0,H 产品- H 料液=0。计算结果如表 7所示。
表 7
Table 7
表 7(Table 7)

表 7 工况5的计算结果
Table 7 Calculating result of the fifth case
|
表 7 工况5的计算结果
Table 7 Calculating result of the fifth case
|
5 结果讨论
选择合适的收敛函数,可把复杂的迭代解法变成简单的Excel公式和函数操作。工况2和工况3的收敛检验函数都为公式(12) ,此函数的优点是函数没有假根、最大或最小值;对于工况2,迭代变量 V / F 限制在0与1之间,以及函数与 V / F 的关系比较接近线形;对于工况3,迭代变量 t 限制在泡点和露点之间的范围内。
利用Excel进行多组分闪蒸计算方便快捷,可大大提高工作效率。“单变量求解”可解决一个公式结果值一定时,变量的引用单元格取值的问题。根据化工问题,设置一个合适的目标函数,根据“单变量求解”功能,寻找满足目标函数最优值的变量值。此功能避免了对人员专业的编程技能的要求,同时解决复杂的试差计算。
 2016, Vol. 37
2016, Vol. 37  Issue(8): 73-77
Issue(8): 73-77  2016, Vol. 37
2016, Vol. 37  Issue(8): 73-77
Issue(8): 73-77