2 齐鲁工业大学山东省制浆造纸科学与技术重点实验室, 济南 250353
2 Key Laboratory of Pulp and Paper Science & Technology, Qilu University of Technology, Jinan 250353, China
拉曼光谱成像是拉曼光谱技术的新发展,结合拉曼光谱检测系统和光学显微镜,将简单的单点分析拓展到对一定范围内样品进行综合分析,以图像呈现样品的化学组分空间分布及表面物理化学性质等信息[1]。由于检测中收集的光谱数量过多,光谱数据处理和分析的难度大。为了解译光谱信息,需借助多元统计学方法,如奇异值分解(SVD)、主成分分析(PCA)等[2]。这类方法能从大数据中分离出化合物光谱,提取特征信息对光谱进行分类研究,探究该化合物的空间分布。然而,这些方法对数据的异常值尤为敏感,原光谱的噪声信号会严重干扰分析结果,造成分离的光谱失真、光谱分类不准确等问题。
在拉曼光谱成像数据中,存在两类难以避免的噪声信号:一是由于系统不稳定或某些样品具有荧光效应而产生的光谱基线漂移现象(Baseline drifts)[3]; 二是由于成像系统中将光信号转换为电信号的电荷耦合器件(CCD)易受到宇宙射线干扰,导致光谱中出现尖锐、随机、正向的干扰峰(Cosmic spike)[4]。人们通常采用光谱处理软件中的定制算法消除这两类噪声信号。常见的基线校正算法有小波变换法[5]、多项式拟合法[6]和导数法[7]等,宇宙射线干扰峰的消除算法主要有中值滤波法和光谱比较法等[8]。,但这些算法存在人为设置参数、去噪结果不稳定、实验可重复性差等问题,去噪过程高度依赖使用者经验,新用户不易操作。如小波变换法设置的母小波与光谱峰形存在差异,会无法拟合光谱峰,导致峰形畸变; 导数法虽无参数设置,但在求导过程中会发生不可逆形变,失真严重。本研究针对现有算法不足,提出了一种新型自适应拉曼光谱成像数据去噪方法,消除了禾本科植物芒草(Miscanthus sinensis)维管束细胞壁拉曼光谱成像数据中的噪声信号(包括9010条光谱),并将结果用于PCA 分析与聚类分析(CA)并重点讨论了不同类型细胞的拉曼光谱特征及相关组分在细胞壁中的分布特点。
2 拉曼光谱成像数据去噪原理 2.1 基线校正拉曼光谱基线校正采用张志敏等提出的自适应迭代惩罚最小二乘法(Adaptive iteratively reweighted penalized least-squares,airPLS)算法[9]。假设x为原光谱构成的n维列向量,z为拟合向量。综合变量Q由z对x的保真度和z自身的粗糙度确定,表达式如下:
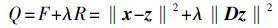
|
(1) |
其中,保真度F为z与x的平方差; 粗糙度R为z的一阶导数(D)平方和; λ为平衡系数,取值越大,拟合向量越平滑。 在保真度中引入对角矩阵W,对角线上的值为权重wi,并求等式(1)的最小有化解:
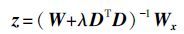
|
(2) |
将等式(2)中特征峰对应的权重设置为wk=0,z即为基线向量。权重向量w可通过获得,预设初始值为w0=1,第次迭代的权重表达式为:
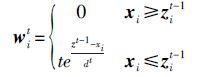
|
(3) |
dt为向量(w-zt-1)中负值元素之和。将第(t-1)次迭代的拟合向量zt-1作为候选基线。当迭代结果满足以下判别式时,输出基线结果。
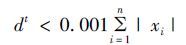
|
(4) |
其中,xi为原光谱向量中的各元素。为节约计算时间,避免死循环,用户需预设最大迭代次数。最后,将原光谱减去基线以输出校正结果。
2.2 宇宙射线干扰峰消除PCA分析作为一种多元统计学方法,已被广泛应用于大型多维数据的分析[10]。该法可消除数据间的线性相关,对多维数据进行降维。基于PCA的这一特点,本研究组开发了一种宇宙射线干扰峰消除算法。先用传统的PCA分析光谱数据,选取能解释85%以上数据信息的载荷向量,将对应的得分作为光谱特征标签。标签间线性无关,可用欧氏距离判断光谱间相似程度。将与原光谱距离最小的光谱视作参考光谱。对参考光谱采用最小二乘法线性拟合以进一步缩小其与原光谱的差异。原光谱与参考光谱之差(残差)作为定位干扰峰的基础,设置阈值以过滤获得干扰峰位置。最后,将原光谱中含有干扰峰的区域用参考光谱替换,输出修正结果。由于参考光谱来自于原数据,因此当原光谱与参考光谱在相同或接近的位置同时存在干扰峰时,可能会出现无法消除某些干扰峰的情况。但是,多次运行干扰峰消除算法即可改善最终的修正结果。
3 实验部分 3.1 原料及样品处理以1年生芒草茎秆为原料(取自国家精准农业研究示范基地,北京),选取高1 m处直径约7 mm样品。 用刀片将样品切削成约3 mm × 3 mm × 5 mm的块状,经去离子水清洗后,用聚乙二醇2000包埋样品。使用滑走切片机(Leica RM2010R)切片,获得厚度约3 μm植物组织横切片,迅速转移至载玻片上,反复用去离子水冲洗以去除可溶于水的包埋剂。最后将样品浸泡于氘代水(D2O)中制得显微镜标本,待测。D2O能削弱样品的荧光效应[11],其拉曼光谱在2500 cm-1附近有明显的D-O伸缩振动峰。
3.2 共聚焦拉曼显微镜检测采用LabRam XploRa共聚焦拉曼显微镜(Horiba Jobin Yvon)对标本的维管束附近区域进行检测。激光波长532 nm,光栅刻线1200,光谱收集器为半导体制冷的CCD,成像扫描步距0.5 μm,光谱获取的累积时间为2 s。以上参数在仪器自带软件LabSpec5中设定。最后将收集的光谱数据转换为TXT文件,导入MATLABTM软件中进行操作与计算,本研究中全部程序可向作者索取。
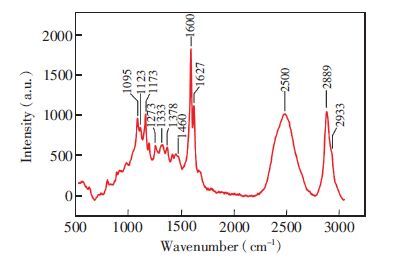
4 结果与讨论 4.1 植物细胞壁拉曼光谱解析分子的各官能团具有特殊的振动能级,在拉曼光谱中表现为波数不同的特征峰[12]。因此,分析特征峰的波数和强度,能获得分子相应的化学结构与含量信息。以芒草细胞壁为例,其平均拉曼光谱(图 1,手动基线校正)具备植物拉曼光谱的一般特征,特征峰主要对应细胞壁中纤维素、半纤维素与木质素的官能团振动能级。其中纤维素与半纤维素的化学结构类似,无法在光谱中将二者区分,因而它们通常被统称为多糖类组分。芒草细胞壁的拉曼特征峰归属见表 1。由于木质素具有苯环结构,光谱在1600 cm-1附近出现强烈振动峰; 典型的多糖类组分特征峰位于2889 cm-1附近,来自—CH和—CH2的伸缩振动。若对光谱中1600和2889 cm-1的特征峰进行成像,可分别获得木质素与多糖类组分含量分布图。根据分布图研究相关组分的沉积与分布规律,有助于阐明细胞壁的化学组成与生物结构间的关系。
|
图 1 芒草细胞壁拉曼光谱 Figure 1 Raman spectrum of Miscanthus sinensis |
4.2 拉曼光谱成像数据去噪
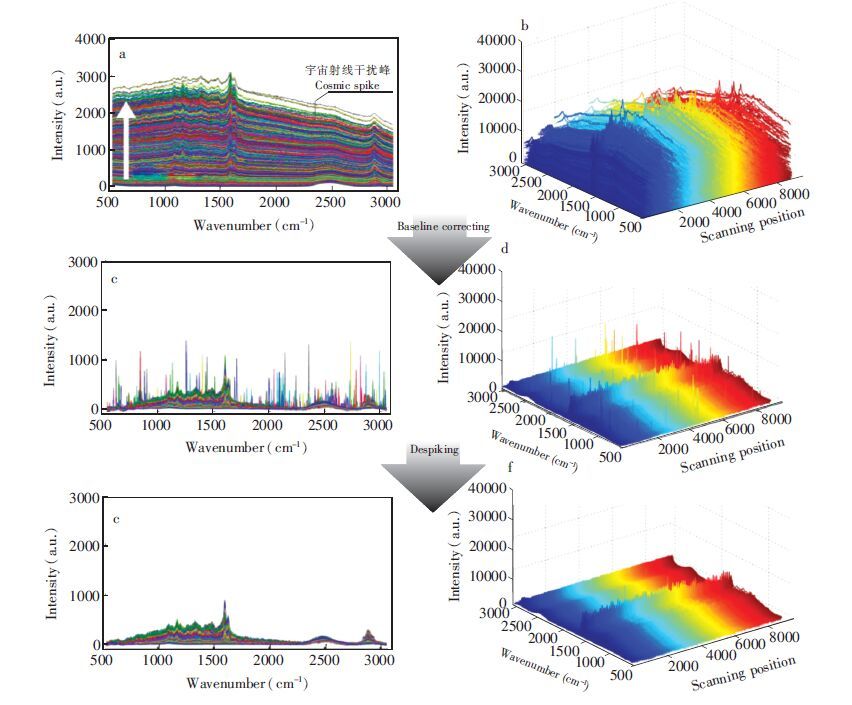
为了验证此去噪方法的可行性,以一组芒草细胞壁拉曼光谱成像数据为例,进行去噪操作。图 2a和2b分别为其二维及三维图像。图中原光谱基线漂移严重,这主要是由植物中木质素受激光激发产生荧光所致[14]。漂移的光谱虽遮挡了大部分宇宙射线干扰峰,但个别强度较大的干扰峰仍清晰可见。经airPLS算法校正基线后的光谱如图 2c和2d所示。与原光谱相比,校正光谱的初始强度均在0附近,光谱未出现形变,同时暴露了原被遮挡的干扰峰。图 2e和2f是经宇宙射线干扰峰消除算法计算后的结果。从图中可知基线漂移与干扰峰问题得到完美解决。
|
图 2 芒草细胞壁拉曼光谱成像数据去噪:原光谱数据二维图(a)和三维图 (b); 基线校正结果二维图(c)和三维图(d); 宇宙射线干扰峰修正结果二维图(e)和三维图(f) Figure 2 Denoising for Raman imaging data of Miscanthus sinensis: 2-D image (a) and 3-D image (b) of original spectral data; 2-D image (c) and 3-D image (d) of baseline corrected results; 2-D image (e) and 3-D image (f) of despiking results |
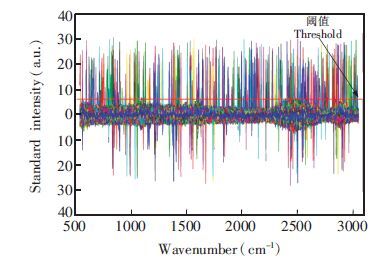
在基线校正算法中,对于高阶使用者,可自行调整平衡系数,设置最大迭代次数(详见2.1节)。通过分析大量数据,综合考虑运算时间成本,设置最大迭代次数为20能得到满意的校正结果,因此建议一般使用者可采用以上两个参数进行计算。当然,由于运算过程中保留了基线向量,此算法的结果可逆,对于校正结果不满意的用户可以选择其它方法进行处理。宇宙射线干扰峰消除算法的可调参数只有过滤干扰峰所用的阈值(详见2.2节)。为保证算法的可重复性,采用光谱自身特性来设置阈值。通过大量研究发现,残差中最弱干扰峰的强度总是大于最强干扰峰1/5,因此本研究将阈值设置为残差数据最大值的1/5(图 3)。当原光谱与参考光谱差异较大时,可能会误判正常的特征峰为干扰峰。但由于使用了参考光谱替换法作为修正方法,参考光谱中保留了正常的光谱特征峰数据,能够最大限度减少修正误差。
|
图 3 芒草细胞壁原光谱与线性拟合光谱残差 Figure 3 Plots of the residual data between original spectra and linear fitting spectra of Miscanthus sinensis |
4.3 拉曼光谱成像数据分类分析
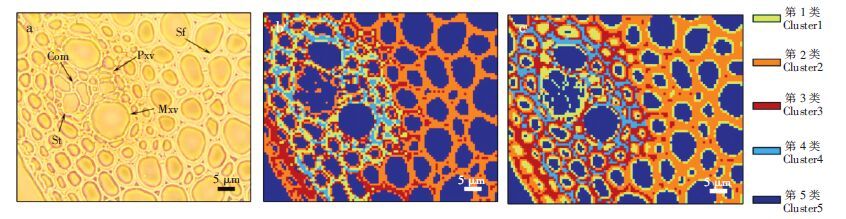
实验采用PCA与CA法对比分析了去噪前后芒草细胞壁的拉曼光谱成像数据(此处选取完整光谱数据进行分析)。在PCA结果中选取能解释85%以上信息的Scores用于CA分析。在实际操作过程中,光谱分类主要受木质素特征峰(1600 cm-1)强度的影响。为更好地对光谱进行分级说明,将光谱分为5类,比较光谱间的差异,并根据分类进行成像,得到的每类光谱具有相似的光谱特征,例如存在相似的特征峰峰位和峰强。图 4a为样品的光学显微镜图像,芒草的维管束由原生木质部导管(Pxv)、后生木质部导管(Mxv)、厚壁纤维细胞(Sf)、筛管(St)和伴胞(Com)构成,其主要承担输导水分、无机盐和有机养料的作用[15]。图 4b和4c分别为原数据与去噪后数据分类结果成像图,图中颜色相同表示相应位置具有类似的光谱特征。理论上,非植物光谱和植物光谱的显著差异可作为区分二者光谱的依据,同时,由于细胞壁的各形态区组分含量不同,植物光谱可进一步细分。但是,图 4b的结果中无法区分细胞壁内侧的植物光谱与非植物光谱。相比之下,图 4c则更有规律,不仅能准确分辨非植物光谱(Cluster 5),还能区分植物光谱(Cluster 1-4)的各个分类。由此可见,去除拉曼光谱成像数据的噪声干扰是准确分类分析光谱的必要前提,本方法能有效解决噪声干扰问题。此外,本方法去噪速度快,并行计算处理9000条光谱的时间不超过3 min。
|
图 4 芒草细胞壁的光学显微镜图像(a),原数据(b)和去噪数据(c)的PCA/CA分析结果成像图 Figure 4 Bright field image of Miscanthus sinensis (a); PCA/CA images of original data (b) and denoising data (c). Pxv: Protoxylem vessel; Mxv: Metaxylem vessel; Sf: Sclerenchyma fiber; St: Sieve tube; Com: Companion cell; Sw: Secondary wall; Cml: Compound middle lamella; Ccml: Cell corner middle lamella. Scale bar = 5 μm. |
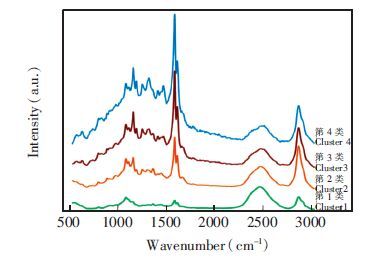
由图 4c中可见,各类光谱呈有层次的环状分布,分类的序号越小则越靠近细胞壁内侧。不同种类细胞中包含不同的光谱类型:Pxv、Mxv及二者周围的Sf由4类光谱共同构成; 远离Pxv和Mxv的Sf由Cluster 3、Cluster 2和Cluster 1光谱组成; St和Com只存在Cluster 2和Cluster 1两类光谱。为进一步比较各类植物光谱,计算了对应的平均光谱(图 5)。从图 5可见,平均光谱木质素特征峰(1600 cm-1)强度由大到小依次为Cluster 4>Cluster 3>Cluster 2>Cluster 1; Cluster 4、Cluster 3和Cluster 2的多糖类组分特征峰(2889 cm-1)强度相近,而在Cluster 1中最小。结合成像图(图 4c)可以发现,同类细胞中靠近细胞壁外侧的木质素含量较高,细胞壁内侧的多糖类组分含量低于其它部分。其次,因Cluster 4只存在于Pxv、Mxv及二者周围的Sf中,这些细胞的木质素含量高于其它类型的细胞,而主要由Cluster 1构成的St和Com中木质素和多糖类组分含量均低于其它细胞类型。此结果与文献[16, 17]对于木质素及多糖类组分在禾本科维管束细胞壁中含量分布特点的描述相符,但本研究的讨论过程更直观,且研究结果具有明确的统计学意义。
|
图 5 去噪数据PCA/CA分类结果的平均光谱 Figure 5 Average spectra of clusters in denoising data PCA/CA results |
5 结 论
本研究提出了一种自适应拉曼光谱成像数据的去噪新方法,能够基于光谱自身特点修正光谱基线漂移和宇宙射线干扰峰噪声,具有输入参数少、光谱失真小、处理速度快、去噪结果稳定等优点。本方法可推广至其它光谱成像数据去噪,经计算机编程后可植入拉曼光谱数据处理软件替代原有的单光谱处理方法,具有广阔的应用前景。采用本方法成功去除了芒草维管束细胞壁拉曼光谱成像数据中的噪声信号,并对去噪后数据进行PCA及CA分析,分析结果优于未去噪的原数据。 研究还发现,同类细胞中木质素含量随细胞壁外侧向内侧递减分布,Pxv、Mxv及二者周围的Sf中木质素含量高于其它细胞类型。下一步工作拟采用多元统计学方法分离植物细胞壁的纯物质光谱,探究其在植物细胞壁中的分布规律。
| 1 |
Gierlinger N, Schwanninger M. Spectroscopy, 2007, 21 :69–89 doi:10.1155/2007/498206 |
| 2 |
Shinzawa H, Awa K, Kanematsu W, Ozaki Y. J. Raman Spectrosc., 2009, 40 (12):1720–1725 doi:10.1002/jrs.v40:12 |
| 3 |
Tan H W, Brown S D. J. Chemometr., 2002, 16 (5):228–240 doi:10.1002/(ISSN)1099-128X |
| 4 |
Hill W, Rogalla D. Anal. Chem., 1992, 64 (21):2575–2579 doi:10.1021/ac00045a019 |
| 5 |
ZHAO Xiao-Yu, FANG Yi-Ming, WANG Zhi-Gang, ZHAI Zhe. Spectroscopy and Spectral Analysis, 2013, 33 (12):3255–3258 赵肖宇, 方一鸣, 王志刚, 翟哲. 光谱学与光谱分析, 2013 ,33(12) :3255–3258 |
| 6 |
FENG Xin-Wei, ZHU Zhong-Liang, SHEN Meng-Jie, CONG Pei-Sheng. Comput. Appl. Chem., 2009, 26 (6):759–762 冯昕韡, 朱仲良, 沈梦洁, 丛培盛. 计算机与应用化学, 2009 ,26(6) :759–762 |
| 7 |
O'Grady A, Dennis A C, Denvir D. Anal. Chem., 2001, 73 :2058–2065 doi:10.1021/ac0010072 |
| 8 |
Ehrentreich F, Sümmchen L. Anal. Chem., 2001, 73 (17):4363–4373 |
| 9 |
Zhang Z M, Chen S, Liang Y Z. Analyst, 2010, 135 (5):1138–1146 doi:10.1039/b922045c |
| 10 |
Geladi P, Grahn H. Multivariate Image Analysis, New York, Wiley, 1997 |
| 11 |
Atalla R H, Agarwal U P. J. Raman. Spectrosc., 1986, 17 :229–231 doi:10.1002/jrs.v17:2 |
| 12 |
Jahncke C L, Paesler M A, Hallen H D. Appl. Phys. Lett., 1995, 67 (17):2483–2485 doi:10.1063/1.114615 |
| 13 |
Wiley J H, Atalla R H. Carbohydr. Res., 1987, 160 :113–129 doi:10.1016/0008-6215(87)80306-3 |
| 14 |
Agarwal U P. Ralph S A. Appl. Spectrosc., 1997, 51 :1648–1655 doi:10.1366/0003702971939316 |
| 15 |
Gierlinger N, Schwanninger M. Plant Physiol., 2006, 140 :1246–1254 doi:10.1104/pp.105.066993 |
| 16 |
Donaldson L A, Radotic K. J. Microsc., 2013, 251 (2):178–187 doi:10.1111/jmi.2013.251.issue-2 |
| 17 |
Ma J F, Zhou X, Ma J, Ji Z, Zhang X, Xu F. Microsc. Microanal., 2014, 20 :956–963 |
| 18 |
Ji Z, Zhang X, Ling Z, Zhou X, Ramaswamy S, Xu F. Biotechnol. Biofuel., 2015, 8 :103 doi:10.1186/s13068-015-0282-3 |
| 19 |
Suzuki K, Kitamura S, Sone Y, Itoh T. Histochem. J., 2002, 34 :535–544 doi:10.1023/A:1026064816129 |
 2016, Vol. 44
2016, Vol. 44


