 图1
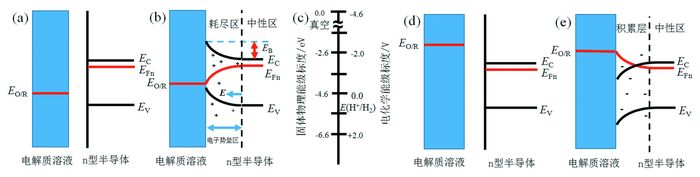
n型半导体/溶液接触前(a, d)和接触后达到平衡状态界面的半导体的空间电荷层(耗尽层b)和半导体的积累层(e),EO/R表示电解质溶液中的氧化还原电对的电极电位,EFn表示n型半导体的费米能级;(c)表示电化学能级标与固体物理能级标的对应关系
Figure1.
Energy band diagram of solution and n-type semiconductor contact. (a, d) not in contact (b, e) In contact under equilibrium EO/R means the potential of redox couples and EFn is the Fermi energy of n-type semiconductor; (c) The corresponding relationship of two energy scale
图1
n型半导体/溶液接触前(a, d)和接触后达到平衡状态界面的半导体的空间电荷层(耗尽层b)和半导体的积累层(e),EO/R表示电解质溶液中的氧化还原电对的电极电位,EFn表示n型半导体的费米能级;(c)表示电化学能级标与固体物理能级标的对应关系
Figure1.
Energy band diagram of solution and n-type semiconductor contact. (a, d) not in contact (b, e) In contact under equilibrium EO/R means the potential of redox couples and EFn is the Fermi energy of n-type semiconductor; (c) The corresponding relationship of two energy scale

Citation: Cui Xiaoli. Flat Band Potential of Semiconductor Electrodes[J]. Chemistry, 2017, 80(12): 1160-1171, 1175.

半导体电极的平带电位
-
关键词:
- 半导体
- / 平带电位
- / 光电化学
- / 光催化
- / Mott-Schottky
English
Flat Band Potential of Semiconductor Electrodes
-
Key words:
- Semiconductor
- / Flat band potential
- / Photoelectrochemistry
- / Photocatalysis
- / Mott-Schottky
-
能源危机和环境污染是当今人类社会发展所面临的两大问题,太阳能的利用包括光电转换太阳能电池、光解水制氢、光催化CO2还原以及光催化技术在环境污染治理方面表现出广泛的应用前景而受到重视,同时也促进了半导体材料、半导体化学、半导体物理以及半导体光电化学的发展。半导体光电化学涉及电化学、半导体物理、光学、半导体材料等多个领域,是研究半导体/溶液界面的光电化学行为及其应用的交叉学科,半导体的光(电)催化活性与其价带以及导带的能级位置密切相关,在半导体光电催化反应的控制中,半导体能级位置的调节是很重要的。
平带电位(Efb)是半导体/电解质溶液体系的重要参数,它是半导体电极特有的、实验可测的物理量,其数值可用于间接“窥探”半导体电极的能级结构。借助吸收光谱或荧光光谱、价电子谱或光电化学方法测定的材料带隙(能级间距),可确定半导体材料的价带与导带能级位置。相对于获得半导体材料的能级结构以及电子性质的其他技术,测量平带电位是一种“原位”研究方法,有助于理解半导体材料在特定的电解质溶液体系中光催化材料的能级特性。
正确理解和应用半导体电极的平带电位是非常必要的,在文献中存在多种平带电位的定义,如平带电位是半导体中的电子能带不随空间位置变化而表现为平带时的半导体/溶液体系的电极电位[1, 2];平带电位是半导体被电子所占据的概率为1/2的能级的电位[3];在光电流-电位图上,平带电位是光电流由负变到正时的电位,即光电流Iph=0时的电极电位。本文分析了半导体电极的能带弯曲及其影响因素,阐明半导体电极平带电位的物理意义及其测定方法,促进面向太阳能新能源的光电转换材料和光催化材料的研究[4, 5]。
1 半导体电极的能带弯曲及其影响因素
1.1 费米能级
单电子近似理论认为,半导体的体材料(晶体)中的电子在周期性排列且固定不动的原子核的势场中运动,其基本特点与自由电子的运动十分相似。半导体中的电子在不同能量的量子态上的分布规律遵从费米分布函数,能量为E的一个量子态被一个电子占据的概率f(E)可写为式(1):
式中,f(E)为电子的费米分布函数,k为玻尔兹曼常数,T是热力学温度,EF为费米能级。从式(1)可以看出,费米能级是被电子所占据的概率为1/2(50%)的能级,它相当于体系的化学势。当半导体处于热平衡状态时,在整个半导体中有统一的费米能级。通俗的理解,固体材料的费米能级反映了电子填充水平的高低。
非简并半导体的载流子浓度相当于稀溶液,比金属或浓溶液中的低5~8个数量级,导带中量子态被电子占据的几率或价带中量子态被空穴占据的几率较小。这时导带中电子的分布或价带中的空穴的分布可以近似地用Boltamann分布函数描述,进一步推导出其费米能级与导带(价带)能级的关系。
对于n型半导体(施主掺杂),当温度不太低时,半导体的费米能级EF与导带底能级EC的关系为[6]:
式中,EF是n型半导体的费米能级,EC是导带底能级,ND是施主杂质浓度,NC为导带有效状态密度。在一般掺杂浓度下,NC>ND,因此式(2)中第二项为负值,这表明n型半导体的EF低于导带底能级EC。在一定的温度下,ND越大(重掺杂),半导体的费米能级EF就越向导带底能级EC靠近。
同样可以写出,在温度不太低时,p型半导体的费米能级EF与价带顶能级Ev的关系为[6]:
式中,EF是p型半导体的费米能级,EV是价带顶能级,NA是受主杂质浓度,NV为价带有效状态密度。在一般掺杂浓度下,NV>NA,式(3)第2项为负值,前面有负号,这表明p型半导体的EF高于价带顶能级EV。NA越大(重掺杂),式(3)第2项越小,p型半导体的费米能级EF就越向价带顶能级EV靠近。
1.2 半导体电极的能带弯曲
半导体电极是对半导体/电解质溶液这样一个整体的简称。20世纪50年代开始,Brattain和Gerisher等以半导体物理中Schottky势垒为基础建立了半导体/电解质溶液界面模型[1]。固体材料的能带理论对于解释金属、半导体、绝缘体材料性质的差异取得了巨大成功。半导体材料是一类特殊的固体材料,其载流子浓度比金属低且能够通过掺杂等方式很容易改变几个数量级;此外,电注入(外加电位)或光注入(适当的光激发)可改变半导体的电子(空穴)占有态能级[6]。近年来人们对半导体电极感兴趣主要基于其在太阳能光电转换体系包括液结的染料敏化太阳能电池、光电分解水制氢、光电还原CO2、光电催化降解污染物等方面的应用。
半导体(固相)与电解质溶液(液相)接触时,半导体/溶液体系达到平衡的条件是半导体界面处的费米能级(EF)与溶液中氧化还原电对的电子的能级(EO/R)相等,即EF=EO/R。受到溶液中氧化还原电对的影响,在半导体侧产生界面区,由于半导体的载流子浓度低,在半导体一侧界面形成空间电荷区(Space charge region),改变载流子分布状态产生能带弯曲,这是不同于金属电极之处。可以看出,由于半导体的费米能级和溶液的氧化还原电对的电极电位差导致能带弯曲和空间电荷区,半导体-金属界面(金-半接触,Schottky势垒)以及不同掺杂类型的半导体界面(如pn结)均存在能带弯曲和空间电荷区。此外,表面态、吸附以及外加电压均会导致半导体的能带弯曲。在溶液一侧则产生类似于金属电极的双电层结构,可分为紧密层(Helmholtz layer)和分散层(Gouy-Chapman layer)。图 1示出一种n型半导体与电解质溶液在接触前(a)和接触后(b)半导体界面耗尽区以及中性区(体内)费米能级的变化情况。
 图1
n型半导体/溶液接触前(a, d)和接触后达到平衡状态界面的半导体的空间电荷层(耗尽层b)和半导体的积累层(e),EO/R表示电解质溶液中的氧化还原电对的电极电位,EFn表示n型半导体的费米能级;(c)表示电化学能级标与固体物理能级标的对应关系
Figure1.
Energy band diagram of solution and n-type semiconductor contact. (a, d) not in contact (b, e) In contact under equilibrium EO/R means the potential of redox couples and EFn is the Fermi energy of n-type semiconductor; (c) The corresponding relationship of two energy scale
图1
n型半导体/溶液接触前(a, d)和接触后达到平衡状态界面的半导体的空间电荷层(耗尽层b)和半导体的积累层(e),EO/R表示电解质溶液中的氧化还原电对的电极电位,EFn表示n型半导体的费米能级;(c)表示电化学能级标与固体物理能级标的对应关系
Figure1.
Energy band diagram of solution and n-type semiconductor contact. (a, d) not in contact (b, e) In contact under equilibrium EO/R means the potential of redox couples and EFn is the Fermi energy of n-type semiconductor; (c) The corresponding relationship of two energy scale
对于给定的半导体,溶液中氧化还原电对的电位EO/R影响半导体的界面能带弯曲程度。例如,n型半导体的费米能级较高,靠近导带,如果高于EO/R (图 1(a)),当半导体与溶液相互接触时电子从半导体流向溶液,这样在半导体一侧的界面,形成正电荷浓度相对高的空间电荷区,半导体中界面层电子的能带向上弯曲,费米能级向下弯曲(图 1(b))。由于半导体的载流子浓度较低,正电荷分散分布(而不是像金属一样集中在表面区),导致在半导体一侧的界面形成空间电荷区,这一点与金属电极是不同的。在该区域内n型半导体的多子(自由电子)转移了(消耗了),因此该区域称为n型半导体的多子耗尽层,该耗尽层为固定的正电荷区,半导体耗尽层的厚度一般为数百纳米量级。同时在空间电荷层产生内建电场,内建电场的方向指向电解质溶液,这样达到平衡后半导体的空间电荷区成为电子的势垒,空穴的势阱。二者初始费米能级差在~1eV量级,半导体界面的内建电场可达105V·cm-1。无机半导体的载流子迁移率在10~1000cm2V-1s-1,该内建电场具有良好的分离光生载流子的能力[5]。
如果n型半导体的费米能级低于电解质溶液的氧化还原电对的电子能级(EO/R较负)(如图 1(d)),当半导体与溶液相互接触时电子从溶液转移到半导体,在半导体一侧界面形成负电荷浓度相对高的空间电荷区,形成多子积累层,半导体界面层中电子的能带向下弯曲,形成电子的反阻挡层,界面处空间电荷区的费米能级上升(图 1(e))。如果n型半导体电极与EO/R足够负的溶液相接触,半导体界面区的费米能级也可能移入导带发生表面简并化,这时半导体/溶液界面成为欧姆接触,其性质与金属电极相似。需要指出的是在半导体的空间电荷区的费米能级也会受到“牵制”而发生弯曲,由于多子的转移而产生弯曲,在界面处与溶液的EO/R相同。半导体内部中性区的能级位置不随溶液中的EO/R的变化而变化,溶液中的EO/R的变化只影响半导体空间电荷层内的费米能级,不会影响耗尽层外中性区半导体费米能级与导带/价带的能级位置。
同一半导体材料,不同的溶液,半导体界面能带弯曲状态不同,这意味着溶液的组成对半导体电极的光电化学特性有重要的影响。
相应地对p型半导体(多子为空穴)可做类似分析。
1.3 外加电位对半导体电极能带弯曲的影响
对于给定的半导体和一定的溶液组成,外加电位(电注入)、光照(光注入)均会影响半导体的载流子浓度及半导体界面的能带弯曲程度。
对半导体电极施加外加电位,本质上是从半导体体系中移出电子(外加正电位,阳极极化),或向体系中注入电子(外加负电位,阴极极化)。对于理想的非简并半导体,相应地改变的是接触界面处半导体的费米能级,对半导体界面处的能带弯曲将产生影响(图 2)。图 2定性地示出了外加电位对n型半导体耗尽层能带弯曲程度及空间电荷层厚度的影响。需要指出的是,改变电极电位导致载流子的注入,能带弯曲程度发生变化,也必然影响界面处的费米能级相对于能级带边的位置。但是,半导体内部(中性区)费米能级相对于导带(价带)能级的位置是不变的[7]。
对于理想的非简并半导体电极,电极电位的变化主要引起空间电荷层中电势的变化以及空间电荷层费米能级的变化,半导体内部中性区的能级位置不随电位的变化而变化,电位的改变只影响半导体空间电荷层的费米能级,不会影响耗尽层外中性区半导体费米能级与导带/价带的位置。因为耗尽层会承担几乎所有外加电位,而中性区不会有电压承担。例如,对于n型半导体的耗尽层(图 2(a)),当外加负电位时,由于电子的注入,受到外加电位的“牵制”,界面层中费米能级升高,同时导致半导体界面能带弯曲程度的减小,空间电荷层厚度的减小(图 2(b))。当外加的负电位达到某一个数值时,能带弯曲消失,空间电荷层厚度为最小,形成平带状态,这时所对应的电位即为半导体电极的平带电位(图 2(c))。继续施加负电位,足够多的电子注入积累在半导体的界面,可形成电子积累层,能带向下弯曲(图 2(d))。继续施加负电位,这时界面层的费米能级有可能移入导带内,形成简并态的表面,此时半导体的行为将向金属行为转变。
对于n型半导体的耗尽层(图 2(a)),当外加正电位时,耗尽层内电子被继续移出,这时半导体能带弯曲程度的增大,空间电荷层厚度的增大(图 2(e))。如果进一步外加正电位,耗尽层势垒进一步提高,这时半导体界面层电子的浓度有可能低于正电荷的浓度,这样在半导体的表面附近形成正电荷浓度较高的界面层,与原n型半导体的多数载流子类型相反的界面层,这就是“反型层”(图 2(f))。
顺便说明,非简并半导体是指载流子浓度较低,电子的分布状态符合玻尔兹曼分布,包括本征半导体和低浓度掺杂的半导体。
1.4 光照对半导体电极能带弯曲的影响
对于孤立的半导体,用能量大于半导体禁带宽度的光照射半导体时,如果光的穿透深度小于空间电荷层厚度,则几乎全部的光子能量被空间电荷层吸收,产生光生载流子,这些光生非平衡载流子的注入改变了体系的载流子浓度,半导体的热平衡状态遭到破坏,这时不再存在统一的费米能级。持续稳定的光照电子-空穴对的产生和复合将处于动态平衡,在半导体内建立新的光照条件下的稳态载流子浓度分布,但导带和价带之间处于不平衡状态,体系偏离原来的费米能级。分别就价带空穴和导带电子讲,它们各自基本上处于平衡状态,费米能级和统计分布函数对导带和价带各自仍然适用,可以分别引入导带费米能级和价带费米能级,这是局部的费米能级,即在光照条件下电子和空穴的准费米能级[1, 6]。导带和价带之间处于不平衡状态,表现为导带电子的准费米能级与价带空穴的准费米能级是不重合的。对于n型半导体,光生空穴浓度显著大于其原始的平衡浓度,空穴的准费米能级更显著偏离原费米能级,而电子的准费米能级则偏离较小,一般在原费米能级附近。
用能量大于半导体禁带宽度的光照射半导体/溶液界面时,光生载流子的产生将影响半导体界面能带弯曲。如果半导体电极处于开路状态,对于n型半导体的耗尽层(图 1b),光生非平衡多子(电子)从价带激发到导带,这些光生的电子将注入到半导体的界面,导致费米能级上升,能带弯曲程度下降,实验上对n型半导体将观察到电极开路电位的负移(图 2b)。对应的,对p型半导体将会观察到电极的开路电位正移。原则上如果用足够强的光照射半导体,足够多的光生载流子的产生和注入,也可能使半导体界面的能带弯曲消失而达到平带状态(图 2c),这时界面内费米能级的弯曲消失。如果半导体电极与金属电极相连,光照时空间电荷层电场导致光生电子/空穴发生漂移运动,半导体界面处的内建电场将分离光生载流子,光生多子移向半导体内部本体,通过外电路到金属电极(可观测到光电流),非平衡少子(空穴)则被扫向表面与溶液中的活性粒子发生界面反应或与表面复合中心复合。(详见3.2的讨论)。
如果光的穿透深度大于空间电荷层厚度,半导体内部的载流子也将被激发跃迁,经过扩散进入到半导体界面层,也会影响载流子的注入和能带弯曲以及光电流的大小。
2 半导体电极平带电位的物理意义及影响因素
2.1 半导体电极平带电位的物理意义
电极电位是指固体/溶液整体的特性,半导体电极的平带电位是指半导体界面能带弯曲为零(平带)时的电极电位。说到底,本质上平带电位就是一个电极电位,具备所有电极电位的基本特性。例如,电极电位是相对值,与所用的参比电极有关。在电化学中规定标准氢电极的电极电位为0,电极电位均为相对于标准氢电极的数值;此外电极电位取决于材料的本性和溶液组成。显然,不同的半导体材料,平带电位不同;同一种半导体材料,不同的溶液,平带电位也不同。
当半导体浸入到溶液中时,半导体与溶液相接触,由于二者能级的差别引起电子流动,以最终达到平衡为终点,因半导体的载流子浓度低导致半导体界面空间电荷层和内建电场的存在,造成半导体界面的能带弯曲。对于理想的非简并半导体电极,外加电位可以调节半导体界面处的费米能级(界面能带弯曲程度)。在一定的电位下,半导体中电子的费米能级能量正好与溶液中的氧化还原电对的电子能级的能量相同,这时没有电荷转移,半导体界面层中没有局部相对过剩电荷,没有空间电荷层,也没有能带弯曲(图 2(c)、表 1b),在这种情况下的电极电位为半导体电极的平带电位[6]。半导体电极的平带电位的值取决于半导体的本体费米能级与溶液电对的氧化还原电位以及Helmholtz层电势降。半导体的本体费米能级受掺杂浓度的影响,而Helmholtz层电势降受表面条件和电解质特性的影响[8]。
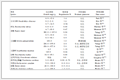 表 1
n型和p型半导体能带弯曲和费米能级与外加电位E和平带电位Efb的关系
Table 1.
Effect of varying the applied potential (E) on the band bending and Femi energy for n-type and p-type semiconductor, respectively
表 1
n型和p型半导体能带弯曲和费米能级与外加电位E和平带电位Efb的关系
Table 1.
Effect of varying the applied potential (E) on the band bending and Femi energy for n-type and p-type semiconductor, respectively
半导体类型 耗尽层(a) 平带条件(b) 积累层(c) n 


p 


平带电位是半导体/溶液体系的特征参数,相当于半导体界面零空间电荷值时的电极电位,当电极电位高于或低于半导体的平带电位数值,反映了半导体空间电荷层的带电状况。表 1是n型和p型半导体能带弯曲、外加电位与平带电位的关系。
平带电位取决于半导体材料本身的特性以及溶液组成,与半导体电极的表面态及其结晶取向有关。例如对于TiO2,不同的晶型[16]、不同的掺杂类型和掺杂浓度均影响其平带电位的数值。不同条件下制备的Ti/TiO2电极其平带电位不同[9]。即使对特定的材料而言平带电位也不是固定的数值,它与溶液有关,它间接地反映了在当时的特定溶液条件下半导体电极的能级特性。换言之,特定半导体的光催化性质和光电催化特性与所处的电解质溶液体系是有关系的。
显然,在处于平带电位的情况下,半导体/溶液体系受到光照时不会有光电流,因为这种状态下界面处光生载流子无法分离。此外,半导体处于平带电位时,半导体的电子的费米能级的能量正好与氧化还原电对的电子的能量(电极电位)相同。或者说平带电位所对应的正好是半导体电极在平带时的费米能级的能量,即Efb=EF(EF为费米能级)[8]。这样测定了体系的平带电位,就可以知道半导体材料的费米能级。
依据半导体电极的平带电位可用来推断电极的带电状况,当电极电位高于(正于)平带电位值(电子被抽走),即E>Efb,即电极电位偏正(类似于阳极极化),对于n型半导体,半导体界面处产生耗尽层,电子的能带向上弯曲,受外加电位的“牵制”半导体界面处空间电荷区费米能级向下弯曲,半导体表面带正电荷。电极电位低于平带电位,即E<Efb,对于n型半导体,半导体界面产生积累层,电子的能带向下弯曲,界面处空间电荷区费米能级向上弯曲,半导体表面带负电荷,足够负的电位在界面处EF可能移入导带内。当E=Efb,半导体的能带不弯曲,即处于平带状态,半导体表面不带电(表 1)。
对于p型半导体,E>Efb,电极电位高于(正于)平带电位值(电子被抽走),即电极电位偏正,电子能带向上弯曲,半导体表面带正电荷,p型半导体的多子是正电荷,这时半导体界面产生正电荷的积累层,受外加电位的“牵制”界面处空间电荷区费米能级向下弯曲;施加足够正的电位时界面处的EF可能移入价带内。当电极电位低于平带电位,即E<Efb,p型半导体界面产生耗尽层,半导体的电子能带向下弯曲,界面处空间电荷区费米能级向上弯曲,半导体表面带负电荷。同样,当E=Efb,半导体的能带不弯曲,处于平带状态,半导体表面不带电(表 1)。
2.2 平带电位与半导体导带或价带能级的关系
通过实验测定了半导体电极的平带电位Efb,由Efb=EF和式(2)和(3)可以导出半导体的导带、价带能级位置与平带电位的关系:
式(2′,3′)分别给出了平带电位与导带以及价带能级的关系。其中的第2项主要取决于半导体的掺杂浓度,掺杂浓度越大,该项数值越小,表明平带电位越接近导带能级(n型半导体)或价带能级位置(p型半导体),一般半导体材料该项数值约为0.1~0.2eV。
例如,对于重掺杂的n型半导体,可以近似认为费米能级是n型半导体的导带底能级,这样对n型半导体而言,平带电位Efb的位置近似于导带底的位置,可以由半导体的禁带宽度Eg及Efb求出其相对应的价带能级EV,需要注意的是,平带电位和半导体的能级标度不同(图 1(c)),换算时需注意统一能级标度。
半导体的费米能级可以从半导体电极的平带电位来估算,在固体物理学中规定真空中电子的能量为零点,依据固体物理学中电子的能级标与电化学电极电势标之间的对应关系可知[1],体系平带电位的负移,意味着半导体费米能级的升高[3],半导体导带能级电位的负移,电子的能级更高,更不稳定,导带的电子更容易失去而发生氧化反应。从溶液一侧而言,溶液中的粒子就更容易得到半导体导带上的电子,发生光还原反应。对于TiO2电极而言,平带电位值越负,从热力学方面,意味着光照后导带上被激发产生的电子具有更强的还原能力,对于水溶液,H2O更容易得到光生电子产生H2,从而有利于提高光催化制氢活性。
2.3 不同溶液中半导体电极平带电位的偏移
平带电位是半导体电极在平带条件下的电极电位,对于特定的半导体,其数值与电解质溶液组成有关。半导体表面与溶液中的氧化还原电对的相互作用可以引起半导体平带电位的明显改变。半导体的表面改性所引起的Efb的变化,也必然影响半导体光电催化反应的热力学可能性。
在半导体光电化学中,电解液的改变使平带电位发生偏移的例子并不少见。例如,在从含Ce3+/Ce4+溶液变为硫酸盐和多硫化合物溶液时,CuIn5S8的平带电位从-0.55V变为-1.20V(vs SCE)[11]。在同一电极上阳离子或阴离子的吸附状况取决于溶液成份,并直接影响电极的平带电位。有文献总结了各种溶液中测定的硅材料的平带电位[8],可以发现半导体材料的平带电位与许多因素有关,包括半导体的掺杂浓度、溶剂类型、电解质类型、氧化还原电对和表面条件以及pH和光照等。最近Gondane等[12]通过引入电解质添加剂调节半导体电极的平带电位,提高了染料敏化太阳能电池的开路电压。
在水溶液中,多数氧化物半导体电极的平带电位与电解质溶液的pH有关[13],氧化物半导体在水溶液中表面被-OH覆盖。例如对于TiO2,存在如下平衡:
在水溶液中,TiO2电极界面反应为:
根据Nernst方程,可写出电极电位与pH的关系:
溶液中的pH的变化影响电极表面的H+解离平衡,并在界面形成表面偶极子(dipole)并产生电位降,使水的氧化或还原的电位整体位移,平带电位随pH的变化为-59mV/pH。pH的变化直接影响着半导体带边电位的移动及半导体材料的光电催化特性。如果半导体电极(例如CdS)与H+无关,则其Efb与pH无关,但溶液中存在相关的离子时(S2-或Cd2+),Efb发生变化。
3 半导体电极平带电位的测定方法
半导体电极的平带电位的重要性在于它是实验可测定的物理量,是联系半导体性质与溶液性质的桥梁,是研究半导体能级性质的有效途径。正是由于半导体能带的弯曲程度受到外加的电位以及光照的影响,这为测定半导体/溶液电极体系的平带电位提供了便利条件。
3.1 半导体电化学方法
Mott-Schottky关系在半导体材料的测试中已得到广泛应用,利用电化学设备所附带的测试软件,可以方便地测得半导体材料的平带电位和载流子浓度,推测空间电荷层的厚度。
半导体电极的电极电位由空间电荷层、Helmholtz层和分散层中的电势差串联而成,当支持电解质浓度较大时可忽略分散层的影响,相应的半导体电极的电容值由空间电荷层电容(Csc)和界面紧密双电层(Helmholtz)电容(CH)构成,可以写为:
式中,C是半导体电极的电容值,Csc是半导体的空间电荷层电容,对于载流子浓度在1015~1018cm-3的半导体Csc约为0.01~数μF·cm-2,小于10μF·cm-2。CH是界面紧密双电层的电容值,一般远大于10μF·cm-2。
由于空间电荷层的厚度(10~100nm)远大于Helmholtz层(0.4~0.6nm)和分散层的厚度(1~10nm),因此界面双电层的影响可以忽略,此时电极电位的变化主要引起半导体空间电荷层中的电势的变化,半导体电极的电容值主要取决于半导体空间电荷层电容,即C≈Csc。这时外加的电极电位的变化将引起半导体能带弯曲的改变,即空间电荷层的厚度的变化以及界面电容的变化。一些电化学专著给出了Mott-Schottky关系的详细的推导[1, 8, 14],对于n型半导体,半导体电极电容值与外加电位的关系可表示为:
对于p型半导体可表示为式(5′),二者相差一负号,
式中,Csc是单位面积半导体电极的电容,Efb是平带电位,E是电极电位,ε为半导体的相对介电常数,ε0为真空介电常数,k为Boltzman常数,T为绝对温度,e为电荷电量。式(5)中,ND是n型半导体中的掺杂施主载流子的浓度,式(5′)中NA是p型半导体中的掺杂受主载流子的浓度。在室温下,kT/e约为0.026V,可以忽略不计,所以在C界面-2-E图中,C界面-2对E的直线部分延长线与电势E轴相交在Efb处,由此得到半导体电极的平带电位Efb。对于n型半导体,斜率为正值;对于p型半导体,斜率为负值。这样就通过Mott-Schottky曲线直线部分的斜率确定半导体膜的多数载流子类型(半导体类型),利用斜率还可以推测载流子浓度以及空间电荷层厚度,从而有助于分析半导体膜的性能,例如研究不锈钢钝化膜的半导体特性[15]。
如果忽略界面Helmholtz双电层电容和分散层电容,并假定半导体的空间电荷层电容符合平板电容器模型,则电容值与半导体的空间电荷层厚度dsc的关系可表示为:
联立式(5,6),可以导出n型半导体空间电荷层的厚度dsc与外加电位E之间的定量关系[16]。
联立式(5′,6)同样可以导出p型半导体空间电荷层的厚度dsc与外加电位E之间的定量关系:
最近,Giorgi等[16]通过实验测定了纳米TiO2电极在不同电位下的空间电荷层厚度,发现在平带电位时对应的空间电荷层厚度最小。
Mott-Schottky关系的应用有特定的前提条件和假设。在n型半导体空间电荷层,正电荷是固定的,完全离子化且均匀分布在空间电荷层。此外,电极较平整时才可以近似为平行板电容器。如果空间电荷层的厚度小于半导体的曲率半径,可近似视为平面。
半导体电极的表面态也会导致能带弯曲影响其电容值,用频率足够高的交流电测定电容值,可减小表面态对电容值的贡献,从而忽略半导体电极表面态的影响,实验中可以测量不同频率下的Mott-Schottky曲线,帮助判断半导体的界面状况。
对于重掺杂半导体,可能存在高密度的表面态以及扩散控制的过程等,即使忽略表面态的影响,Helmholtz界面双电层的电势降也较显著,这时利用Mott-Schottky曲线测定平带电位会有较大的误差。实际样品的电化学测量实验往往观察到Mott-Schottky曲线偏离直线,测定得到的电容值与所用的交流电的频率有关。平带电位的数值与交流频率有关,这反映了半导体材料的特殊状态。例如,对于阳极氧化得到的TiO2纳米管电极其Efb随测试频率的增加而降低,经过热处理后在不同的频率下样品的平带电位的数值相对一致[16]。非理想的Mott-Schottky曲线预示着半导体的结构与性质的复杂性,还有可能与存在表面膜有关[14, 17]。
利用Mott-Schottky曲线测定平带电位,外加电位时需要注意的是半导体的稳定性。例如,对于氧化物半导体,在外加正电位时是相对稳定的,因此电位扫描时宜从正到负,避免外加负电位时半导体被还原导致电极被破坏,平带电位数据失真。此外利用光电化学方法测定平带电位并相互比对,有助于得到确切的平带电位数值。
基于晶体单电子近似的固体能带理论成功地解释了半导体的体材料的光电化学实验现象,依据半导体/溶液界面半导体能带弯曲产生耗尽层的Mott-Schottky理论和Bulter光电流理论也得到认可和广泛应用,但是该模型忽略了界面双电层(Helmholtz和分散层)的影响,忽略了耗尽层中载流子的复合以及界面反应速度,这些方法仅在一定范围是适用的。
3.2 半导体光电化学方法
半导体吸收光能导致电子从低能级跃迁到较高的能级,假设半导体电极不存在表面态,且光电流的大小由半导体内光生载流子的传输速度控制,基于这两个假设,Bulter首先提出了半导体电极的光电流理论[18],后续的一些专著或教材均依此阐明半导体电极光电流的产生[8, 14]。半导体材料/溶液体系的光致电荷分离主要发生在半导体与溶液接触时所形成的空间电荷层(耗尽层),以n型半导体形成的耗尽层为例,空间电荷层的内建电场方向为由本体指向表面(溶液一侧),空间电荷层的内建电场可以分离电子和空穴。受空间电荷区内建电场的作用在此区域中的电子将倾向于自发的流向半导体内部(本体)一侧,而空穴自发的向半导体的表面集中。空间电荷层内的光生空穴迁移到半导体表面而与溶液中的粒子发生氧化反应;光生的电子由半导体表面向体相(半导体内)迁移(图 3(a))。在有辅助电极存在的条件下,光生载流子通过外电路到达金属辅助电极并进行还原反应,两电极间出现通过外电路而形成的光电流(图 3(b))。当半导体电极处于耗尽层状态,在一定光照强度下,光电流取决于材料的光吸收系数α(与光的波长有关)、少数载流子的扩散长度Lp(取决于材料的完整性)、空间电荷层的厚度dsc(和外加电位有关)和界面电化学反应过程。这是半导体固液结光电化学太阳能电池的基本原理。如果采用水溶液,当半导体导带的电位比水的还原电位负,光生电子受内建电场作用流向本体通过外电路在辅助电极上与H2O发生还原反应得到H2;与此同时,如果价带能级电位比水的氧化电位正,光生空穴被内建电场扫向溶液界面在半导体电极上和H2O反应产生O2,这样可利用半导体电极实现光电化学分解水(Photoelectro-chemical water splitting),这是光电催化分解水制氢的基本原理。通过测定短路光电流数值(即控制半导体电极与对电极之间的电位差为0V时的光电流),可以表征半导体电极的光电化学分解水的活性。半导体电极光分解水的活性与半导体的光吸收(载流子的产生)、载流子的分离效率以及界面反应速率直接相关。当然,施加电位(bias)能够改变半导体界面空间电荷区的能带弯曲程度(图 2)和载流子的分离效率从而影响水的分解效率。
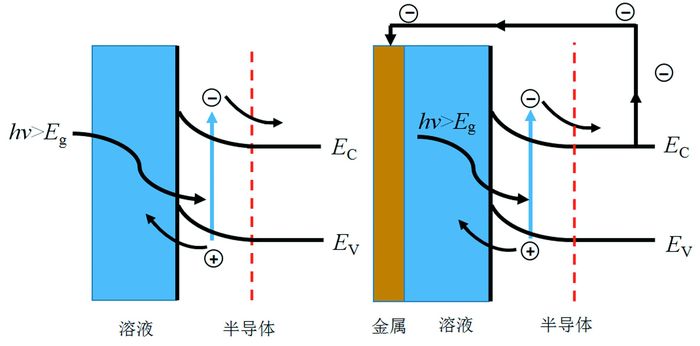 图3
光照n型半导体(耗尽层)/溶液界面光生载流子的产生及运动方向(a)和光电流的产生(b)(示意图未标示扩散区)
Figure3.
Production and charge transfer of electron-hole pairs under light illumination (a) and photocurrent can be observed for a n-type semiconductor (depletion layer) and solution junction with the assistance of metal counter electrode (b)
图3
光照n型半导体(耗尽层)/溶液界面光生载流子的产生及运动方向(a)和光电流的产生(b)(示意图未标示扩散区)
Figure3.
Production and charge transfer of electron-hole pairs under light illumination (a) and photocurrent can be observed for a n-type semiconductor (depletion layer) and solution junction with the assistance of metal counter electrode (b)
材料的光吸收系数α定义为:
式中,α是与光强度无关的比例系数,为光吸收系数,α与光的频率有关,即材料对不同波长的光的吸收能力是不同的,且与固体能带间跃迁类型有关,x是在光材料中的传播距离(光的穿透深度),I是光强度,I0是入射光的强度,α与光子能量hν的关系为:
式中,A为常数,n取决于跃迁类型,n=1/2是直接跃迁,n=2为间接跃迁。测定半导体材料的吸收光谱,利用(αhν)1/n对hν作图可确定半导体材料的禁带宽度Eg[19],有文献将该图称为Tauc图[20]。
通常认为半导体电极的光电流分两部分,一是光生载流子在耗尽层内建电场作用下产生的电流,二是在准中性区由光生载流子的扩散产生的电流[8, 14, 18],半导体电极光电流Iph的表达式为:
如果αLp≪1,在αdsc≪1的电位范围内,
由式(11)可知,半导体电极的光电流与(dsc+Lp)成正比,光电流受入射光的波长(体现在光吸收系数α)影响,且与空间电荷层的厚度dsc和少子的扩散长度Lp有关,dsc取决于决定空间电荷层厚度的电位。
对于强吸收(较小的光穿透深度α-1),αdsc≫1 (α-1≪dsc),由式(10)则有:
这时光电流与电位无关,所有产生的光生载流子全部贡献于光电流,与掺杂浓度和电位无关。
在一定的外加电位下,可得式(12):
给定外加的电极电位,测定在不同波长(hν)的单色光光照时半导体电极的光电流,可得到Iph-hν关系图,这就是光电流作用谱;(Iphhν)1/n对hν作图可得到一条直线,在hν轴上的截距为半导体的光电化学禁带宽度Eg。
光照下半导体电极光电流的产生与能带弯曲程度密切相关,从1.3节的分析可知,外加电位影响半导体的能带弯曲以及空间电荷层的厚度进而影响光电流的大小。图 2示出了n型半导体外加负电位(阴极极化)时能带弯曲的减小,到平带和积累层的变化过程。可以推测对于n型半导体外加正电位(阳极极化)时,能带弯曲程度增大(图 2(e)),空间电荷层厚度增加,必然提高n型半导体电极的光电流。
使用一定波长的入射光照射半导体电极时,改变半导体电极上施加的电位,对于n型半导体,当施加的电位比平带电位负时,光生电荷不能转移到外电路,因而不能形成光电流;相反,当施加的电位比平带电位正时,存在能带弯曲与空间电荷层,就能够产生光电流。外加电位影响半导体电极的暗电流与光电流,光电流(Iph=Ilight-Idark)刚刚产生时电极上施加的电位就是半导体的平带电位[9],因此平带电位还可以通过测量光电流的起始电位来估算[21]。
根据Gartner-Butler理论,以n型半导体为例,光电流密度(Iph)与电极电位(E)的定量关系可以表示为[18]:
式中,ε0是真空介电常数,ε是半导体的相对介电常数,ND是n型半导体中的掺杂施主载流子的浓度,I0是入射光强度,E是电极电位。在给定波长和一定强度的光照射下,测定外加不同电极电位下的光电流数值,利用光电流的平方Iph2与电极电位E作图,得到一条直线,将直线外推至Iph2为0,由截距得到平带电位,由斜率可得到半导体的载流子浓度。例如,刘玲等[2]利用该关系测定了聚吡咯半导体电极的平带电位。
在暗态下,通过测定半导体电极的Mott-Schottky关系曲线,利用直线部分的切线在横轴的截距可以方便地得出平带电位,但在直线部分不是很理想的情况下作切线具有一定的随意性,会产生人为的误差。光电化学法测量的平带电位为开始产生光电流的电位,施加电位可以准确给出,通过仪器直接读出光电流数值,可避免人为因素产生的误差。但是测定光电流的光电化学方法需要逐步调试外加电位,测定在不同外加电位下的光电流密度,相比于测定Mott-Schottky曲线,实验工作量较大。
3.3 光谱电化学方法
电极电位高于或低于平带电位值,反映了半导体电极空间电荷层的带电状况(表 1)。以n型半导体TiO2为例说明,当电极电位高于平带电位值,偏正(表 1),半导体/溶液界面产生耗尽层,半导体表面带整正电。例如对于TiO2电极在780nm处的吸光度没有变化。当电极电位低于平带电位值,偏负(表 1),产生电子的积累层,能带向下弯曲,当给TiO2薄膜电极施加负偏压时,积累的电子与TiO2反应导致生成Ti3+,这时TiO2电极在780nm处的吸光度将急剧上升,吸光度开始上升时对应的电极电位就是纳米晶半导体电极的平带电位。戴松元等利用光谱电化学的方法研究了TiO2电极的平带电位[22],利用这种方法可以推测纳米结构半导体电极的平带电位[10, 22, 23]。该方法测定的是材料的吸光度的变化,该方法的灵敏度以及得到的平带电位的数值的可比性相对较差。
3.4 开路光电压方法(饱和光电位方法)
用hν≥Eg的光照射处于平衡的半导体电极时,将产生光生载流子的注入,光生载流子的注入导致能带弯曲程度发生变化,产生光电势,这是半导体界面处费米能级发生变化的宏观标志。当入射光足够强时(例如大于500mW/cm2),足够多的载流子的产生和注入将使能带弯曲消失达到平带状态,此时测得的开路光电位即为平带电位。在一般的光电化学实验中,当光强再增加50%,开路光电位的变化极小,即认为达到饱和,达到最大值,该值可认为是平带电位[24, 25]。这是估算平带电位的简单方法。
4 纳米结构半导体电极的平带电位
纳米材料是当今新材料的主流,一般认为纳米是指1~100 nm的尺度范围,纳米材料是指在三维空间有一维处于纳米尺度范围内且具有特殊性质的材料,纳米材料的内涵十分丰富,包括零维的纳米粒子、纳米晶等,一维的纳米材料有纳米棒、纳米线、纳米管、纳米带等,二维的纳米材料有纳米片、纳米薄膜等。空间电荷层的厚度约为10~100 nm,正好处于纳米材料的尺度范围。由于纳米粒子的尺寸小,纳米结构半导体/电解质溶液不能像半导体的体材料一样能够形成能带弯曲,纳米结构半导体电极的自建场很小,其表面的能带弯曲可以忽略不计[10]。这种电极光生的载流子依靠载流子的浓度梯度的扩散形成电流。纳米多孔膜电极的电荷传输特性与传统的块体半导体不同。在纳米多孔膜电极中,能带不弯曲,电子在纳米粒子导带上可向两个方向流动,电子在导带内的传输依靠电子浓度扩散控制,通过测量空间电荷层电容的变化来测量半导体的平带电位数值有一定的误差。通过光谱电化学方法测量半导体纳米晶电极的平带电位似乎应更为准确。
Mott-Schottky理论和Bulter光电流理论均是基于半导体的体材料/电解质溶液界面的半导体界面能带弯曲产生耗尽层建立的,原则上这些理论并不适用于纳米结构的半导体电极,如果纳米材料的特征尺寸大于空间电荷层的厚度,仍可近似视为体材料。实际上利用Mott-Schottky曲线测定半导体电极的平带电位非常方便,在许多文献中仍然对纳米结构半导体电极如纳米管[16, 19, 26~28]、纳米棒[21, 29]、纳米片[13]、纳米晶[30]等直接应用Mott-Schottky关系测定其平带电位[31~33]。Munoz[28]发现,TiO2膜和TiO2纳米管的Efb值不同且与纳米管的长度有关,TiO2膜的Efb值为-0.725V,1μm长的TiO2纳米管的Efb值移至-0.33V(测试频率3Hz,pH=6)。对于纳米结构半导体电极建议利用不同测试方法进行测试,利用Mott-Schottky关系测定其平带电位时建议采用高频(例如大于1kHz)以减少漏电得到较准确的平带电位数值。
5 结语
太阳能的开发利用是当今科学界面临的重大的课题,对于解决能源危机、保护地球环境具有重要意义。半导体光电化学是具有鲜明的理论和实际意义的重要学科,其实际应用则正是致力于研究新型固液结太阳能电池和解决能源与环境问题。例如基于半导体与电解液接触后形成固液结的新型太阳能电池如染料敏化太阳能电池,由于其成结容易,制作简单而受到广泛关注。对于光电催化降解溶液中的染料污染物或者是光电催化分解水制氢或光电催化还原CO2,也是半导体与溶液的复杂体系,通过测定平带电位深入认识体系的能级状况,将为判断半导体的光电催化活性提供有益的参考。光电化学方法主要研究在光照的情况下与电解液接触的半导体材料产生的光电化学现象,是一种原位研究手段,可以得到一些表面分析与化学方法所不能得到的半导体材料的信息,还广泛用于半导体材料特性的测试、金属腐蚀产物分析以及机理研究等方面。
本文分析了半导体/溶液界面的能带弯曲及其影响因素,给出了光照下半导体电极的光电流的产生以及与电极电位的关系,解释了平带电位的物理意义,总结了测定半导体材料的平带电位多种方法,并穿插介绍了平带电位的应用,如确定半导体材料的能级、载流子浓度、判断半导体类型等。测定平带电位可为半导体材料的研究与应用提供理论依据,促进其在太阳能电池、光电催化制氢以及光电催化降解污染物等方面的研究与应用。在当今能源危机与环境污染的大背景下,面向太阳能开发利用的半导体光电化学将会受到更广泛的重视和得到更大的发展。
-
-
[1]
查全性等著. 电极过程动力学(第2版). 北京: 科学出版社, 1987, P499, P512.
-
[2]
刘玲, 赵尧敏, 杨洁等.物理化学学报, 2006, 22(3):261~264. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=wlhxxb200603001
-
[3]
赵景茂, 谷丰, 赵旭辉等.物理化学学报, 2008, 24(1):147~151.
-
[4]
C Jiang, S J A Moniz. A Wang et al. Chem. Soc. Rev., 2017, 46, 4645~4660. doi: 10.1039/C6CS00306K
-
[5]
M G Walter, E L Warren, J R McKone et al. Chem. Rev., 2010, 110:6446~6473. doi: 10.1021/cr1002326
-
[6]
刘恩科, 朱秉升, 罗晋生编著. 半导体物理学(第7版). 北京: 电子工业出版社, 2011, P71, P75.
-
[7]
Z Zhang, J T Yates Jr. Chem. Rev., 2012, 112:5520~5551. doi: 10.1021/cr3000626
-
[8]
章小鸽编著, 张俊喜, 张大全, 徐群杰等译. 硅及其氧化物的电化学-表面反应、结构和微加工. 北京: 化学工业出版社, 2004, P67.
-
[9]
S Fukumoto, M Kitano, M Takeuchi et al. Catal. Lett., 2009, 127:39~43. doi: 10.1007/s10562-008-9769-x
-
[10]
姜月顺, 李铁津. 光化学. 北京: 化学工业出版社, 2004, P301~302.
-
[11]
B Scrosati, L Fornarini, G Razzini et al. J. Electrochem. Soc., 1985, 132(3):593~598. doi: 10.1149/1.2113912
-
[12]
V Gondane, P Bhargava. Electrochim. Acta, 2016, 209:293~298. doi: 10.1016/j.electacta.2016.05.079
-
[13]
P Xu, T J Milstein, T E Mallouk. ACS Appl. Mater. Interf., 2016, 8:11539~11547. doi: 10.1021/acsami.6b02901
-
[14]
吴辉煌主编. 电化学. 北京: 化学工业出版社, 2004, P23, P169.
-
[15]
林玉华, 杜荣归, 胡融刚等.物理化学学报, 2005, 21(7):740~745. http://www.wanfangdata.com.cn/details/detail.do?_type=perio&id=wlhxxb200507009
-
[16]
L Giorgi, E Salernitano, T D Makris et al. Thin Solid Films, 2016, 601:28~34. doi: 10.1016/j.tsf.2015.11.078
-
[17]
S R莫里森著, 吴辉煌译. 半导体与金属氧化膜的电化学. 北京: 科学出版社, 1988.
-
[18]
M A Butler. J. Appl. Phys. 1977, 48:1914~1920. doi: 10.1063/1.323948
-
[19]
Y Yan, J Lee, X Cui. Vacuum, 2017, 138:30~38. doi: 10.1016/j.vacuum.2016.12.049
-
[20]
J Lim, P Murugan, N Lakshminarasimhan et al. J. Catal., 2014, 310:91~99. doi: 10.1016/j.jcat.2013.05.014
-
[21]
W Yang, Y Oh, J Kim et al. ACS Appl. Mater. Interf., 2016, 8(1):425~431. doi: 10.1021/acsami.5b09241
-
[22]
戴俊, 胡林华, 刘伟庆等.物理学报, 2008, 57(8):5310~5316. doi: 10.7498/aps.57.5310
-
[23]
T S Kang, K H Chun, J S Hong et al. J. Electrochem. Soc., 2000, 147(8):3049~3053. doi: 10.1149/1.1393646
-
[24]
古列维奇等著, 彭端伍译. 半导体光电化学. 北京: 科学出版社, 1989, P89.
-
[25]
钱士元, 钱道荪, 孙璧媃.化学学报, 1983, (9):769~775. http://www.cnki.com.cn/Article/CJFDTotal-HXXB198309000.htm
-
[26]
M X Sun, X L Cui. Electrochem. Commun., 2012, 20:133~136. doi: 10.1016/j.elecom.2012.04.016
-
[27]
Y Cong, H S Park, S Wang et al. J. Phys. Chem. C, 2012, 116(27):14541~14550. doi: 10.1021/jp304340a
-
[28]
A G Munoz. Electrochim. Acta, 2007, 52:4167~4176. doi: 10.1016/j.electacta.2006.11.035
-
[29]
J Su, J Wang, C Liu et al. RSC Adv., 2016, 6:101745~101751. doi: 10.1039/C6RA22895J
-
[30]
D Xiong, Q Zhang, Z Du et al. New J. Chem., 2016, 40:6498~6504. doi: 10.1039/C6NJ00253F
-
[31]
T Giannakopoulou, I Papailias, N Todorova et al. Chem. Eng. J., 2017, 310:571~580. doi: 10.1016/j.cej.2015.12.102
-
[32]
F S B Kafi, K M D C Jayathileka, R P Wijesundera et al. Phys. Status Solid B, 2016, 253(10):1965~1969. doi: 10.1002/pssb.201600288
-
[33]
P Shahbazi, A Kiani. Int. J. Hydrogen Energy, 2016, 41(39):17247~17256. doi: 10.1016/j.ijhydene.2016.07.080
-
[1]
-
图 1 n型半导体/溶液接触前(a, d)和接触后达到平衡状态界面的半导体的空间电荷层(耗尽层b)和半导体的积累层(e),EO/R表示电解质溶液中的氧化还原电对的电极电位,EFn表示n型半导体的费米能级;(c)表示电化学能级标与固体物理能级标的对应关系
Figure 1 Energy band diagram of solution and n-type semiconductor contact. (a, d) not in contact (b, e) In contact under equilibrium EO/R means the potential of redox couples and EFn is the Fermi energy of n-type semiconductor; (c) The corresponding relationship of two energy scale
(注:示意图忽略了耗尽区与中性区之间的扩散区)
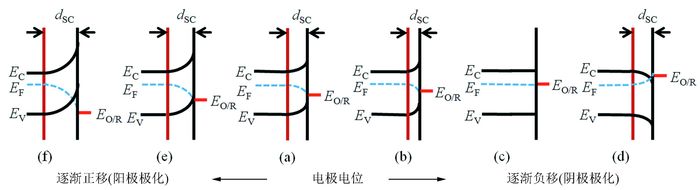
图 2 改变电极电位EO/R对n型半导体能带弯曲程度及空间电荷层厚度的影响
Figure 2 Effect of varying the applied potential on the band bending, EF and dsc are the Fermi energy and thickness of depletion region for n-type semiconductor, respectively
图中分别表示n型半导体耗尽层(a)和外加负电位(b),以及外加负电位达到平带状态(c)和达到积累层能带位置(d),外加正电位(e)耗尽层厚度增大,进一步加大达到反型层(f);dsc表示空间电荷层的厚度;图中显示外加电位时半导体费米能级的变化, EO/R表示电极电位
图 3 光照n型半导体(耗尽层)/溶液界面光生载流子的产生及运动方向(a)和光电流的产生(b)(示意图未标示扩散区)
Figure 3 Production and charge transfer of electron-hole pairs under light illumination (a) and photocurrent can be observed for a n-type semiconductor (depletion layer) and solution junction with the assistance of metal counter electrode (b)
表 1 n型和p型半导体能带弯曲和费米能级与外加电位E和平带电位Efb的关系
Table 1. Effect of varying the applied potential (E) on the band bending and Femi energy for n-type and p-type semiconductor, respectively
半导体类型 耗尽层(a) 平带条件(b) 积累层(c) n 


p 


-

 扫一扫看文章
扫一扫看文章
计量
- PDF下载量: 2949
- 文章访问数: 54489
- HTML全文浏览量: 29674


 下载:
下载:


 下载:
下载:

