English

• 1   引言

  狄尔斯–阿尔德反应(Diels-Alder reaction, 简称D-A反应)是[4+2]环化反应中最具代表性的、由共轭双烯与亲双烯体构建环己烯骨架的经典反应, 通常具有良好的立体和区域选择性, 并持续受到人们的关注和重视^[1~7].从目前所能查阅到的文献看, 一部分D-A反应以协同方式进行, 即反应只需要经历一个六元环过渡态就可形成最终产物^[8~14].但随着该领域的不断发展, 也有一些D-A反应被发现是通过分步方式完成的^[15~20].比如Yang等^[15]通过理论计算, 发现反式茴香脑和异戊二烯的D-A反应就是以分步方式进行的.另外, D-A反应过程的电子特性通常存在两种可能:正常电子需求的D-A反应(Normal-Electron-Demand Diels-Alder Reaction, NEDDA, 反应中双烯体提供电子)和逆电子需求的D-A反应(Inverse-Electron-Demand Diels-Alder Reaction, IEDDA, 反应中亲双烯体提供电子), 且双烯体和亲双烯体上带有不同的取代基会对反应的产率、反应速率等带来不同程度的影响^[21~26].

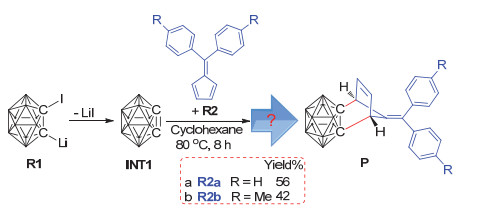
  受苯炔能与双烯发生D-A反应的实验事实所启发, 2014年7月, 由谢作伟教授^[27]带领的研究小组发现: 1-碘-2-锂邻碳硼烷(图 1中R1)能在环己烷溶剂中、80 ℃条件下与亚甲基环戊二烯衍生物(R2)发生D-A反应, 并得到一系列结构新颖的碳硼烷基降冰片烯衍生物, 而且得到的碳硼烷基降冰片烯衍生物可进一步与多种物质反应转化为在医药和材料等学科领域具有潜在应用价值的功能碳硼烷衍生物^{[28, 29]}.实验发现:当使用二苯基亚甲基环戊二烯为双烯体时, 反应进行8 h后的分离产率最高可达56%(图 1中反应a); 而如果在亚甲基环戊二烯的苯环上带有4-Me取代基时, 产率降低到42%(图 1中反应b).作者还对其他一系列取代基进行了测试, 发现其产率与R＝H相比都有不同程度的降低, 这说明反应底物上的取代基对该反应存在着重要影响, 但目前其影响机制尚不明确, 也未看到关于该反应中双烯上的取代基如何影响反应产率的理论解释.另外, 从现有的实验事实很难判断1-碘-2-锂邻碳硼烷与亚甲基环戊二烯衍生物的D-A反应是分步过程还是协同机制, 也不清楚该反应中的电子流动是趋向于正常电子需求的D-A反应还是趋于逆电子需求的D-A反应.所有这些问题都有赖于开展进一步的理论研究来提供更详细的信息.

  图1 1-碘-2-锂-邻碳硼烷与亚甲基环戊二烯衍生物的Diels-Alder反应(为清晰起见, 除关键位置的氢原子外, 其余氢原子已全部省略) Figure1. Diels-Alder reactions between 1-iodo-2-lithio-o-carborane and fulvenes (all hydrogen atoms, except for those are essential for understanding, are omitted for clarity)

  图选项

  下载全尺寸图像

  下载幻灯片

  鉴于D-A反应的重要意义及碳硼烷基降冰片烯衍生物在化学、医药、材料等学科领域的潜在应用价值, 本论文采用密度泛函理论(DFT)的B3LYP方法^{[30, 31]}, 使用Gaussian 09程序^[32]对图 1所示的1-碘-2-锂邻碳硼烷与亚甲基环戊二烯衍生物的D-A反应开展了理论研究, 在探讨该反应的微观机理和取代基效应的基础上, 借助自然键轨道理论(NBO)^[33~35]对关键过程的电子特性进行分析和讨论, 以期进一步拓宽该反应的应用范围、为实验上制备更多有价值的碳硼烷衍生物提供有意义的理论参考.

  2   结果与讨论

  2.1   反应机理

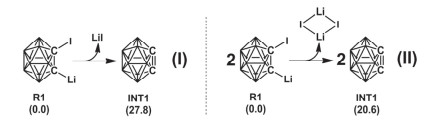
  根据文献报道^{[27, 36~39]}, 1-碘-2-锂邻碳硼烷在反应中可首先脱去一分子LiI形成碳硼炔中间体INT1, 之后该碳硼炔中间体INT1与加入的亚甲基环戊二烯(R2a)反应, 经过一系列过程生成碳硼烷衍生物P(图 1).经计算, 由一分子1-碘-2-锂邻碳硼烷前体脱去LiI形成碳硼炔中间体INT1的过程约需要吸收27.8 kcal·mol^－1的能量, 而由两分子1-碘-2-锂邻碳硼烷前体脱去菱形LiI二聚体形成碳硼炔中间体INT1则只需要吸收约20.6 kcal·mol^－1的能量(图 2), 这在80 ℃的实验条件下是比较容易实现的.

  图2 在IDSCRF-B3LYP/DZVP计算水平上、由R1形成INT1的Gibbs自由能(kcal·mol^－1)变化(为清晰起见, 图中所有氢原子已全部省略) Figure2. Relative Gibbs free energies (in kcal·mol^－1) for the formation of INT1 from R1, obtained at IDSCRF-B3LYP/DZVP level (all hydrogen atoms are omitted for clarity)

  图选项

  下载全尺寸图像

  下载幻灯片

  为了探讨该反应中碳硼烷基降冰片烯衍生物的形成机制, 我们首先采用密度泛函理论的B3LYP方法, 对INT1和R2a反应形成碳硼烷基降冰片烯衍生物Pa的反应机理进行了计算, 结果如图 3所示.

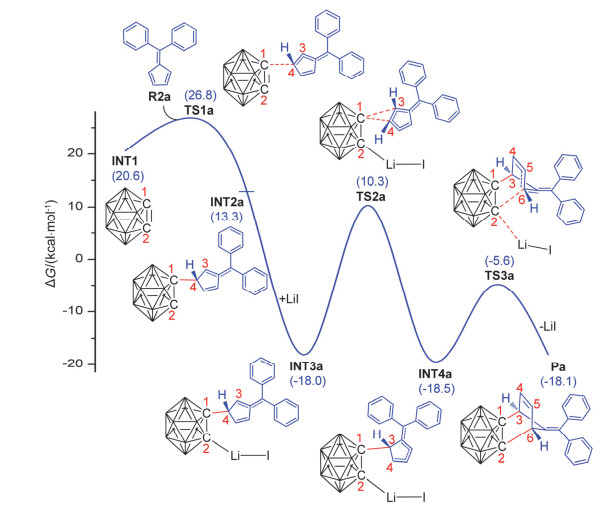  图3 在IDSCRF-B3LYP/DZVP计算水平上得到的INT1与R2a的反应机理和相对Gibbs自由能(能量单位: kcal·mol^－1; 为清晰起见, 除关键位置的氢原子外, 其余氢原子已全部省略) Figure3. Reaction mechanisms and relative Gibbs free energies (in kcal·mol^－1) for reaction between INT1 and R2a, obtained at the IDSCRF-B3LYP/DZVP computational level (all hydrogen atoms, except for those are essential for understanding, are omitted for clarity)

  图选项

  下载全尺寸图像

  下载幻灯片

  活泼的碳硼炔中间体INT1首先与加入的亚甲基环戊二烯衍生物R2a反应, 通过过渡态TS1a转化为另一个中间体INT2a, 该过程在环己烷溶剂中需要越过的自由能垒仅为6.2 kcal·mol^－1, 比较容易被克服.在中间体 INT2a中, 由于受R2a分子片段的影响, C(2)上聚集了较多的负电荷(NPA电荷值为－0.511, 图 4), 所以反应体系中的LiI倾向于重新与C(2)结合形成更稳定的中间体INT3a.从图 3中可以看出: LiI与中间体INT2a的结合为自发过程, 放出31.3 kcal·mol^－1的能量, 该步对于驱动整个反应的进行起着至关重要的作用.之后中间体INT3a中的碳硼烷基通过1, 2-σ迁移、越过28.3 kcal·mol^－1的自由能垒转化为中间体INT4a.最后, 中间体INT4a中的C(2)与C(6)原子不断靠近, 越过过渡态TS3a实现关环, 在形成最终产物Pa的同时掉下一分子的LiI.关环过程需要越过的自由能垒较低, 仅为12.9 kcal·mol^－1.

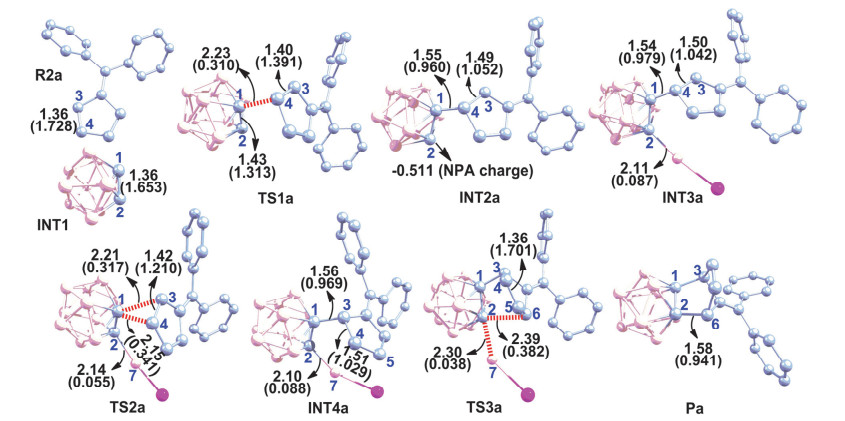  图4 在IDSCRF-B3LYP/DZVP计算水平上优化得到的关键驻点的结构参数(键长: Å)和相应的Wiberg bond index (WBI)指数(为清晰起见, 图中所有的氢原子已全部省略) Figure4. Key structural parameters (with bond lengths in Å) and Wiberg bond index (WBI) for optimized stationary points, obtained at the IDSCRF-B3LYP/DZVP computational level (all hydrogen atoms are omitted for clarity)

  图选项

  下载全尺寸图像

  下载幻灯片

  纵观整个反应过程, 碳硼炔中间体INT1与亚甲基环戊二烯衍生物R2a需要经历三个过渡态(TS1a~TS3a)才能形成碳硼烷衍生物Pa, 其中TS2a对应的自由能垒为28.3 kcal·mol^－1, 对反应的总速率具有决定性影响.考虑到TS2a高出反应起始物约10.3 kcal·mol^－1, 且所对应的自由能垒远高于TS1a和TS3a(分别为6.2 kcal·mol^－1和12.9 kcal·mol^－1), 我们认为与TS2a对应的1, 2-σ迁移过程是整个反应过程的速率决定步骤(决速步).当实验温度为80 ℃时, 中间体INT3a通过过渡态TS2a的速率常数为2.217×10^－5 s^－1, 相应的反应半衰期为8.7 h.该结果与“反应时间为8 h得到56%的硼烷基降冰片烯衍生物Pa”的实验事实很好吻合.若实验温度为50 ℃, 则中间体INT3a通过过渡态TS2a的速率常数减小为4.785×10^－7 s^－1, 这可能是实验温度降低到50 ℃后, 反应8 h仅得到23%的硼烷基降冰片烯衍生物Pa的原因.该结果还可较好解释在50 ℃条件下、当反应时间延长至48 h之后, 产率重新回升至52%的实验结果^[27].我们也曾尝试过其他可能的反应路径如协同机理、LiI二聚体辅助的反应机理等(详见补充材料图S2~S4及相应的文字说明), 但综合现有的计算结果, 图 3所示的路径为该反应的最有可能路径.

  在IDSCRF-B3LYP/DZVP计算水平上优化得到的各关键驻点的几何构型参数如图 4所示.为了深入探讨反应路径上各驻点的成键特性, 我们还在相同计算水平上, 利用Gaussian09内嵌的NBO程序对这些结构中关键位置的电荷布居和Wiberg成键指数(Wiberg Bond Index, WBI)进行了计算(图 4).

  在INT1中, C(1)—C(2)之间的键长为1.36 Å, 相应的WBI值为1.653, 具有典型的不饱和键特征, 之后随着R2a中C(4)原子的靠近, C(1)—C(4)之间通过TS1a成键形成中间体INT2a.在过渡态TS1a中, C(1)—C(4)之间的键长为2.23 Å, 相应的WBI值为0.310, 同时C(1)—C(2)之间的键长拉长至1.43 Å, 相应的WBI值减小为1.313.由于C(1)—C(4)的成键, 中间体INT2a中C(3)—C(4)之间的键长由R2a中典型的C＝C双键(1.36 Å)拉长至1.49 Å, 具有C—C单键的特征. TS1a中C(3)—C(4)的键长为1.40 Å, 具有部分双键的性质^{[10, 40, 41]}, 说明C(3)上的部分正电荷已经被离域化, 对TS1a起到了稳定作用, 这可能是TS1a的自由能垒仅为6.2 kcal·mol^－1的主要原因之一.

  经计算, INT2a中C2原子堆积了－0.511的负电荷, 为整个结构中负电荷聚集最多的地方.因此LiI碎片会重新与C(2)结合, 并通过该过程有效降低了INT2a的相对能量(图 3).在INT3a中, C(2)—Li的键长为2.11 Å, 相应的WBI值为0.087, 说明C(2)和Li之间的确存在一定的成键作用.之后, 随着TS2a中C(1)—C(4)键的拉长和C(1)—C(3)键的同步缩短, 带着LiI的碳硼烷基完成1, 2-σ迁移过程, 转化为与一般D-A分步反应所形成的中间体类似的INT4a^[15~20].在INT4a中, C(1)—C(3)的键长为1.56 Å, 相应的WBI值为0.969, 说明C(1)和C(3)之间已形成C—C单键.同时, C(2)—Li的键长(2.10 Å)和相应的WBI值(0.088)与INT3a相比无明显变化.随着INT4a中C(6)和C(2)原子的进一步靠近, INT4a将在形成C(2)—C(6)键的同时脱去LiI分子碎片, 并形成最终产物Pa.该过程中, 由于C(4)—C(5)之间形成了C＝C双键(1.36 Å), 分子中不存在未成对电子, 所以TS3a的能量较低, 其自由能垒也仅为12.9 kcal·mol^－1.

  2.2   取代基效应

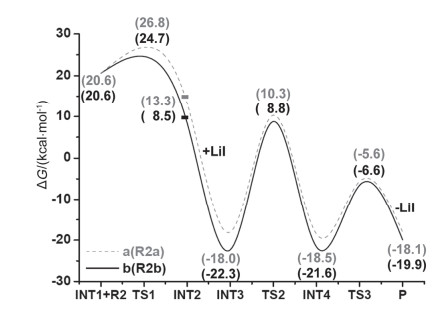
  实验中发现, 在80 ℃条件下, 当在亚甲基环戊二烯R2a的苯环上带有4-Me取代基时, 经相同的反应时间后, 产率比4-H取代的情况有明显下降(图 1), 这说明苯环上的取代基对该反应的产率具有一定的影响.为了探索R2中苯环上的取代基对反应产率的影响, 我们接着对4-Me取代的反应(图 1中反应b)进行了理论计算, 发现该反应的反应机理与反应a类似: INT1和R2b之间的反应同样需要经历三个过渡态(TS1b~TS3b)才能形成最终产物Pb.计算得到的反应b的势能剖面图如图 5所示.为了方便比较, 在图 5中还以虚线给出了反应a的势能剖面图曲线.

  图5 在IDSCRF-B3LYP/DZVP计算水平上得到的INT1与R2b的反应机理和相对Gibbs自由能(kcal·mol^－1) Figure5. Reaction mechanisms and relative Gibbs free energies (in kcal·mol^－1) for reaction between INT1 and R2b, obtained at the IDSCRF-B3LYP/DZVP computational level

  图选项

  下载全尺寸图像

  下载幻灯片

  从图 5可以看出, 计算得到的反应b(4-Me取代)的整个势能面都位于反应a(4-H取代)的势能面下方, 即反应b的中间体、过渡态和产物的相对能量都比反应a中相应结构的能量略低.反应b中三个过渡态TS1b、TS2b、TS3b对应的活化自由能垒依次为4.1、31.1和15.0 kcal·mol^－1, 说明从INT3b到INT4b的转化过程仍然为反应b的决速步, 与反应a的结论一致.由于INT3b相对于INT3a的降低值大于TS2b相对于TS2a的降低值, TS2b的活化自由能垒(31.1 kcal·mol^－1)相对于TS2a的活化自由能垒(28.3 kcal·mol^－1)升高了2.8 kcal·mol^－1, 使相同条件下反应b的速率常数相对于反应a减小了约50倍.该计算结果与使用R2b为反应底物时产率明显降低的实验事实基本吻合, 较好地预测和重现了取代基更替时反应产率的变化趋势.

  为了考察苯环上的取代基对该反应的影响, 我们接着对反应a和b中自TS1之后的所有结构进行了NBO分析.计算结果显示:在反应a中, TS1a、INT2a、INT3a、TS2a、INT4a和TS3a中的R2a分子片段上都分布有部分正电荷(+0.425~+0.981), 其余分子片段则带有相应数值的负电荷(见补充材料图S5, S6).而在反应b中, 上述六个结构中的两个CH₃上都不同程度地带有部分正电荷(+0.074~+0.120), 这表明CH₃对苯环产生了给电子效应.由于CH₃的给电子效应对INT3b的稳定化作用大于对TS2b的稳定化作用, 从而使TS2b对应的自由能垒与TS2a相比略有升高.

  2.3   电子结构特征

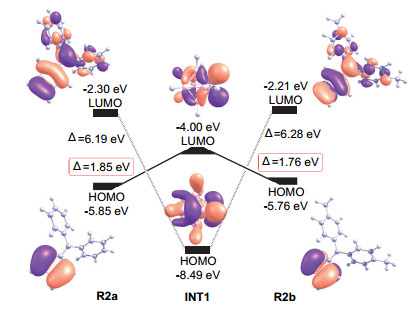
  为了探索该D-A反应过程中的电子流动特征, 我们对碳硼炔中间体INT1和反应物R2a、R2b的前线轨道进行了计算, 得到的INT1、R2a和R2b的前线轨道及其能量结果如图 6所示.从图 6可以看出:无论以R2a还是R2b为底物, LUMO_(INT1)-HOMO_(R2)的能量差(对应R2a和R2b依次为1.85 eV和1.76 eV)均小于LUMO_(R2)-HOMO_(INT1)的能量差(对应R2a和R2b依次为6.19 eV和6.28 eV)).这说明在INT1与R2反应时, 双烯(R2)倾向于提供电子而碳硼炔(INT1)倾向于得到电子, 符合正常电子需求的D-A反应(NEDDA)特征.同时, 由于R2b中苯环上CH₃基团的给电子效应, 使得R2b的HOMO轨道能量与R2a相比略有升高, 因此INT1与R2b的反应相对容易, TS1b的活化自由能垒相对于TS1a降低了2.1 kcal·mol^－1 (图 5).

  图6 INT1与R2(a, b)的前线轨道及其能量(单位: eV) Figure6. Frontier orbitals and corresponding energies (in eV) of INT1 and R2(a, b)

  图选项

  下载全尺寸图像

  下载幻灯片

  为进一步确认该反应的正常电子需求(NEDDA)电子流动特征, 我们接着对其他几个反应底物(R2c~R2e)的前线轨道进行了计算, 相应的结果整理在表 1中.从中不难看出:不论R2的苯环上是带有吸电子基团还是给电子基团, 其LUMO_(INT1)-HOMO_(R2)的能量差都小于LUMO_(R2)-HOMO_(INT1)的能量差.这说明该反应中, 双烯(R2)的确倾向于提供电子而碳硼炔(INT1)倾向于得到电子, 即该反应更趋向于正常电子需求的D-A反应(NEDDA)特征, 与前面关于R2a和R2b的研究结论一致.

  表 1  INT1与R2c~R2e的前线轨道能量(eV) Table 1.  Frontier orbital energies (in eV) of INT1 and R2c~R2e

  表选项

  导出Excel

  下载全尺寸表图像

  	HOMO	LUMO	ΔE(1)a	ΔE(2)b
  INT1	－8.49	－4.00
  R2c	－5.68	－2.12	1.68	6.37
  R2d	－6.24	－2.81	2.24	5.68
  R2e	－5.99	－2.45	1.99	6.04
  aΔE(1)＝[LUMO(INT1)－HOMO(R2)]; bΔE(2)＝[LUMO(R2)-HOMO (INT1)].

  3   结论

  通过使用DFT密度泛函理论在IDSCRF-B3LYP/DZVP计算水平上对1-碘-2-锂-邻碳硼烷与亚甲基环戊二烯衍生物的Diels-Alder反应开展理论研究, 可以得出以下结论:

  (1) 该反应以分步方式而不是协同方式进行.碳硼烷基降冰片烯衍生物的形成需要经过一个碳硼烷基的1, 2-σ迁移过程, 该过程为整个反应的决速步.在IDSCRF-B3LYP/DZVP计算水平上预测的半衰期与相应的实验条件和产率较好吻合.

  (2) 无论亚甲基环戊二烯衍生物的苯环上带有给电子基团还是吸电子基团, 该反应中的亚甲基环戊二烯衍生物作为双烯都扮演电子供体角色, 在反应中提供电子给碳硼炔, 即该反应与正常电子需求的D-A反应(NEDDA)具有相似的电子流动特征.

  我们的理论研究结果对于进一步改进实验条件和提高反应产率具有一定的借鉴意义.

  4   计算细节

  除非另有说明, 本论文中所涉及到的所有计算都是使用Gaussian 09^[32]程序中的B3LYP方法^{[30, 31]}完成的, 基组用的都是双-ζ全电子基组(double-ζ valence polarized basis set, DZVP)^{[42, 43]}.对于所计算的每一个反应, 都保留了原实验中的结构而未做任何简化.为了考虑环己烷溶剂对反应的影响, 我们在计算中使用了自洽反应场(SCRF)的极化连续介质模型(PCM)^[44]和我们组之前所提出的IDSCRF半径^[45], 在此标记为IDSCRF模型.文中所报道的所有能量均为使用THERMO程序^[46]矫正到实验温度(353 K)条件下的Gibbs自由能.为了确保过渡态所连接的两个中间体的正确性, 我们还使用内禀反应坐标分析(IRC)方法^[47~49]对相应的过渡态进行了分析确认(见补充材料图S7).另外, 我们还使用自然键轨道理论(NBO)^[33~35]对特定的结构做了前线轨道和电子特性分析.

  最后, 为了衡量B3LYP方法结果的可靠性, 我们使用B3LYP-D3^{[50, 51]}、ωB97xD^[52]、和M06-2X^[53]方法在相同计算水平上对反应a的最优路径进行了计算(见补充材料表S1).从表S1中可以看出:采用B3LYP-D3、ωB97xD和M06-2X计算方法得到的决速步能垒(TS2a)与实验值相比明显偏低, TS1a的自由能垒甚至变为负值, 与之前在对四嗪与环烯烃的[4+2]环加成反应的理论研究中观察到的现象类似^[8].可能是由于计算误差间的相互抵消, 在该体系中, 采用B3LYP方法预测的半衰期和反应速率与相应的反应时间和产率数据最为吻合, 与我们之前对镍催化碳硼炔与炔烃的[2+2+2]环化反应的研究结论基本一致^[54].因此, 本论文正文中用于讨论的数据都是基于B3LYP计算方法得到的.

• 1. [1]

     Li, Y.; Li, W.; Zhang, J. Chem. Eur. J. 2017, 23, 467. doi: 10.1002/chem.201602822

  2. [2]

     Pellissier, H. Chem. Rev. 2016, 116, 14868. doi: 10.1021/acs.chemrev.6b00639

  3. [3]

     Wei, L.; Wang, C.-J. Chem. Commun. 2015, 51, 15374. doi: 10.1039/C5CC06465A

  4. [4]

     艾文英, 廖道红, 雷晓光, 有机化学, 2015, 35, 1615. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=yjhu201508003&dbname=CJFD&dbcode=CJFQAi, W.; Liao, D.; Lei, X. Chin. J. Org. Chem. 2015, 35, 1615(in Chinese). http://kns.cnki.net/KCMS/detail/detail.aspx?filename=yjhu201508003&dbname=CJFD&dbcode=CJFQ

  5. [5]

     刘文香, 吴宇强, 李灵芝, 李霞, 有机化学, 2016, 36, 1501. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=yjhu201607005&dbname=CJFD&dbcode=CJFQLiu, W.; Wu, Y.; Li, L.; Li, X. Chin. J. Org. Chem. 2016, 36, 1501(in Chinese). http://kns.cnki.net/KCMS/detail/detail.aspx?filename=yjhu201607005&dbname=CJFD&dbcode=CJFQ

  6. [6]

     Cao, M.-H.; Green, N. J.; Xu, S.-Z. Org. Biomol. Chem. 2017, 15, 3105. doi: 10.1039/C6OB02761J

  7. [7]

     Xie, M.; Lin, L.; Feng, X. Chem. Rec. 2017, 17, 1. http://www.ncbi.nlm.nih.gov/pubmed/28508470

  8. [8]

     方德彩, 陈彦梅, 化学学报, 2014, 72, 253. http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hxxb201402014&dbname=CJFD&dbcode=CJFQFang, D.; Chen, Y. Acta Chim. Sinica 2014, 72, 253(in Chinese). http://kns.cnki.net/KCMS/detail/detail.aspx?filename=hxxb201402014&dbname=CJFD&dbcode=CJFQ

  9. [9]

     Ran, Y.; Tang, M.; Wang, Y.; Wang, Y.; Zhang, X.; Zhu, Y.; Wei, D.; Zhang, W. Tetrahedron 2016, 72, 5295. doi: 10.1016/j.tet.2016.06.057

  10. [10]

      Musavi, S. M.; Amani, J.; Omidian, N. Tetrahedron 2014, 70, 708. doi: 10.1016/j.tet.2013.11.089

  11. [11]

      Li, Y.; Fang, D.-C. Phys. Chem. Chem. Phys. 2014, 16, 15224. doi: 10.1039/c4cp02068e

  12. [12]

      唐敏, 吴永, 刘源, 蔡茂强, 夏飞, 刘顺英, 胡文浩, 化学学报, 2016, 74, 54. doi: 10.7503/cjcu20150436Tang, M.; Wu, Y.; Liu, Y.; Cai, M.; Xia, F.; Liu, S.; Hu, W. Acta Chim. Sinica 2016, 74, 54(in Chinese). doi: 10.7503/cjcu20150436

  13. [13]

      Yang, Y.-F.; Liang, Y.; Liu, F.; Houk, K. N. J. Am. Chem. Soc. 2016, 138, 1660. doi: 10.1021/jacs.5b12054

  14. [14]

      Duan, A.; Yu, P.; Liu, F.; Qiu, H.; Gu, F. L.; Doyle, M. P.; Houk, K. N. J. Am. Chem. Soc. 2017, 139, 2766. doi: 10.1021/jacs.6b12371

  15. [15]

      Yang, Y.; Liu, Q.; Zhang, L.; Yu, H.; Dang, Z. Organometallics 2017, 36, 687. doi: 10.1021/acs.organomet.6b00886

  16. [16]

      Li, Y.; Du, S. RSC Adv. 2016, 6, 84177. doi: 10.1039/C6RA16321A

  17. [17]

      Diamond, O. J.; Marder, T. B. Org. Chem. Front. 2017, 4, 891. doi: 10.1039/C7QO00071E

  18. [18]

      Ess, D. H.; Jones, G. O.; Houk, K. N. Adv. Synth. Catal. 2006, 348, 2337. doi: 10.1002/(ISSN)1615-4169

  19. [19]

      Yu, P.; Yang, Z.; Liang, Y.; Hong, X.; Li, Y.; Houk, K. N. J. Am. Chem. Soc. 2016, 138, 8247. doi: 10.1021/jacs.6b04113

  20. [20]

      Yu, P.; Li, W.; Houk, K. N. J. Org. Chem. 2017, 82, 6398. doi: 10.1021/acs.joc.7b01132

  21. [21]

      Pellissier, H. Adv. Synth. Catal. 2016, 358, 2194. doi: 10.1002/adsc.v358.14

  22. [22]

      Mojica, M.; Méndez, F.; Alonso, J. A. Molecules 2016, 21, 200. doi: 10.3390/molecules21020200

  23. [23]

      Oliveira, B. L.; Guo, Z.; Bernardes, G. J. L. Chem. Soc. Rev. 2017, 46, 4895. doi: 10.1039/C7CS00184C

  24. [24]

      Fell, J. S.; Lopez, S. A.; Higginson, C. J.; Finn, M. G.; Houk, K. N. Org. Lett. 2017, 19, 4504. doi: 10.1021/acs.orglett.7b02064

  25. [25]

      Liu, F.; Liang, Y.; Houk, K. N. J. Am. Chem. Soc. 2014, 136, 11483. doi: 10.1021/ja505569a

  26. [26]

      Levandowski, B. J.; Zou, L.; Houk, K. N. J. Comput. Chem. 2016, 37, 117. doi: 10.1002/jcc.24191

  27. [27]

      Zhang, J.; Qiu, Z.; Xu, P.-F.; Xie, Z. ChemPlusChem 2014, 79, 1044. doi: 10.1002/cplu.201402129

  28. [28]

      Tang, C.; Xie, Z. Angew. Chem., Int. Ed. 2015, 54, 7662. doi: 10.1002/anie.201502502

  29. [29]

      (a) Lyu, H.; Quan, Y.; Xie, Z. Angew. Chem., Int. Ed. 2015, 54, 10623; (b) Lyu, H.; Quan, Y.; Xie, Z. J. Am. Chem. Soc. 2016, 138, 12727.

  30. [30]

      Lee, C.; Yang, W.; Parr, R. G. Phys. Rev. B 1988, 37, 785. doi: 10.1103/PhysRevB.37.785

  31. [31]

      Becke, A. D. J. Chem. Phys. 1993, 98, 5648. doi: 10.1063/1.464913

  32. [32]

      Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. A.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H. P.; Izmaylov, A. F.; Bloino, J.; Zheng, G.; Sonnenberg, J. L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Montgomery, J. A., Jr.; Peralta, J. E.; Ogliaro, F.; Bearpark, M.; Heyd, J. J.; Brothers, E.; Kudin, K. N.; Staroverov, V. N.; Keith, T.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, J. M.; Klene, M.; Knox, J. E.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Zakrzewski, V. G.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Dapprich, S.; Daniels, A. D.; Farkas, O.; Foresman, J. B.; Ortiz, J. V.; Cioslowski, J.; Fox, D. J. Gaussian 09, Revision D.01, Gaussian, Inc., Wallingford, CT, 2013.

  33. [33]

      Reed, A. E.; Curtiss, L. A.; Weinhold, F. Chem. Rev. 1988, 88, 899. doi: 10.1021/cr00088a005

  34. [34]

      Reed, A. E.; Weinstock, R. B.; Weinhold, F. J. Chem. Phys. 1985, 83, 735. doi: 10.1063/1.449486

  35. [35]

      Carpenter, J. E.; Weinhold, F. J. Mol. Struct. 1988, 169, 41. doi: 10.1016/0166-1280(88)80248-3

  36. [36]

      Zhao, D.; Zhang, J.; Xie, Z. Angew. Chem., Int. Ed. 2014, 53, 12902. doi: 10.1002/anie.201409141

  37. [37]

      Qiu, Z.; Xie, Z. Dalton Trans. 2014, 43, 4925. doi: 10.1039/C3DT52711E

  38. [38]

      Wang, S. R.; Xie, Z. Organometallics 2012, 31, 4544. doi: 10.1021/om300324n

  39. [39]

      Qiu, Z.; Ren, S.; Xie, Z. Acc. Chem. Res. 2011, 44, 299. doi: 10.1021/ar100156f

  40. [40]

      Dang, Y.; Qu, S.; Tao, Y.; Song, C.; Wang, Z. X. J. Org. Chem. 2014, 79, 9046. doi: 10.1021/jo501399x

  41. [41]

      Dub, P. A.; Béthegnies, A.; Poli, R. Organometallics 2012, 31, 294. doi: 10.1021/om2009149

  42. [42]

      Godbout, N.; Salahub, D. R.; Andzelm, J.; Wimmer, E. Can. J. Chem. 1992, 70, 560. doi: 10.1139/v92-079

  43. [43]

      Sosa, C.; Andzelm, J.; Elkin, B. C.; Wimmer, E.; Dobbs, K. D.; Dixon, D. A. J. Phys. Chem. 1992, 96, 6630. doi: 10.1021/j100195a022

  44. [44]

      Miertus, S.; Scrocco, E.; Tomasi, J. Chem. Phys. 1981, 55, 117. doi: 10.1016/0301-0104(81)85090-2

  45. [45]

      Tao, J.-Y.; Mu, W.-H.; Chass, G. A.; Tang, T.-H.; Fang, D.-C. Int. J. Quantum Chem. 2013, 113, 975. doi: 10.1002/qua.24065

  46. [46]

      Fang, D.-C. THERMO, Beijing Normal University, Beijing, China.

  47. [47]

      Gonzalez, C.; Schlegel, H. B. J. Chem. Phys. 1989, 90, 2154. doi: 10.1063/1.456010

  48. [48]

      Gonzalez, C.; Schlegel, H. B. J. Phys. Chem. 1990, 94, 5523. doi: 10.1021/j100377a021

  49. [49]

      Fukui, K. Acc. Chem. Res. 1981, 14, 363. doi: 10.1021/ar00072a001

  50. [50]

      Grimme, S. J. Comput. Chem. 2006, 27, 1787. doi: 10.1002/(ISSN)1096-987X

  51. [51]

      Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. J. Chem. Phys. 2010, 132, 154104. doi: 10.1063/1.3382344

  52. [52]

      Chai, J.-D.; Head-Gordon, M. Phys. Chem. Chem. Phys. 2008, 10, 6615. doi: 10.1039/b810189b

  53. [53]

      Zhao, Y.; Truhlar, D. G. J. Phys. Chem. 2006, 110, 5121. doi: 10.1021/jp060231d

  54. [54]

      Mu, W. H.; Xia, S. Y.; Li, J. X.; Fang, D. C.; Wei, G.; Chass, G. A. J. Org. Chem. 2015, 80, 9108. doi: 10.1021/acs.joc.5b01464

• 

  图 1  1-碘-2-锂-邻碳硼烷与亚甲基环戊二烯衍生物的Diels-Alder反应(为清晰起见, 除关键位置的氢原子外, 其余氢原子已全部省略)

  Figure 1  Diels-Alder reactions between 1-iodo-2-lithio-o-carborane and fulvenes (all hydrogen atoms, except for those are essential for understanding, are omitted for clarity)

  下载: 全尺寸图片 幻灯片
  

  图 2  在IDSCRF-B3LYP/DZVP计算水平上、由R1形成INT1的Gibbs自由能(kcal·mol^－1)变化(为清晰起见, 图中所有氢原子已全部省略)

  Figure 2  Relative Gibbs free energies (in kcal·mol^－1) for the formation of INT1 from R1, obtained at IDSCRF-B3LYP/DZVP level (all hydrogen atoms are omitted for clarity)

  下载: 全尺寸图片 幻灯片
  

  图 3  在IDSCRF-B3LYP/DZVP计算水平上得到的INT1与R2a的反应机理和相对Gibbs自由能(能量单位: kcal·mol^－1; 为清晰起见, 除关键位置的氢原子外, 其余氢原子已全部省略)

  Figure 3  Reaction mechanisms and relative Gibbs free energies (in kcal·mol^－1) for reaction between INT1 and R2a, obtained at the IDSCRF-B3LYP/DZVP computational level (all hydrogen atoms, except for those are essential for understanding, are omitted for clarity)

  下载: 全尺寸图片 幻灯片
  

  图 4  在IDSCRF-B3LYP/DZVP计算水平上优化得到的关键驻点的结构参数(键长: Å)和相应的Wiberg bond index (WBI)指数(为清晰起见, 图中所有的氢原子已全部省略)

  Figure 4  Key structural parameters (with bond lengths in Å) and Wiberg bond index (WBI) for optimized stationary points, obtained at the IDSCRF-B3LYP/DZVP computational level (all hydrogen atoms are omitted for clarity)

  下载: 全尺寸图片 幻灯片
  

  图 5  在IDSCRF-B3LYP/DZVP计算水平上得到的INT1与R2b的反应机理和相对Gibbs自由能(kcal·mol^－1)

  Figure 5  Reaction mechanisms and relative Gibbs free energies (in kcal·mol^－1) for reaction between INT1 and R2b, obtained at the IDSCRF-B3LYP/DZVP computational level

  下载: 全尺寸图片 幻灯片
  

  图 6  INT1与R2(a, b)的前线轨道及其能量(单位: eV)

  Figure 6  Frontier orbitals and corresponding energies (in eV) of INT1 and R2(a, b)

  下载: 全尺寸图片 幻灯片

  表 1  INT1与R2c~R2e的前线轨道能量(eV)

  Table 1.  Frontier orbital energies (in eV) of INT1 and R2c~R2e

  	HOMO	LUMO	ΔE(1)a	ΔE(2)b
  INT1	－8.49	－4.00
  R2c	－5.68	－2.12	1.68	6.37
  R2d	－6.24	－2.81	2.24	5.68
  R2e	－5.99	－2.45	1.99	6.04
  aΔE(1)＝[LUMO(INT1)－HOMO(R2)]; bΔE(2)＝[LUMO(R2)-HOMO (INT1)].

  下载: 导出CSV
•