English

• 

  1   引言

  近年来, 过渡金属硫化物 (TMS) 广泛应用于工业生产与生物科学等领域^[1~5], 受到人们越来越多的关注.例如VIB族的钼硫化物在固体润滑剂、储氢材料以及工业催化等方面有着重要应用^[6~13].其中, 以MoS₂作为主催化成分的催化剂已实现在加氢脱硫 (HDS) 等石油炼制过程中的商业化应用^{[14, 15]}.此外, 钼硫化物的价格相对低廉、储量丰富, 可以代替贵金属 (如铂族贵金属), 应用于电催化析氢反应 (HER) 等过程中^[16~19].相比VIB族的钼硫化物, 与其相邻的VB族铌硫化物在超导^{[20, 21]}、离子电池^[22]、湿度传感器^[23]、催化材料^[24]等方面也有着大量的研究.在1-丁烯的异构化和氢化反应中, NbS₂起到了很好的催化效果^[25].而且作为一种非常有应用前景的氢处理 (HDT) 催化材料, 它在很多反应中甚至表现出了比传统的钼硫化物更高的催化活性^[26].有研究表明在氢处理 (HDT) 反应中它们的催化活性表现出如下强弱顺序: NbS₃＞NbS₂＞Nb_1+xS₂＞MoS₂^[27~31].虽然铌硫化物表现出比钼硫化物更高的催化活性, 但由于铌硫化物的天然矿物储量少, 合成时前驱体硫化困难, 且铌硫化物在空气中容易被氧化^[32], 因而大大限制了铌硫化物的商业化应用与研究.不过, 有研究表明将铌硫化物掺杂到传统的NiMo硫化物催化剂中可显著提高其催化活性^[33].这也说明了同族金属间掺杂或毗邻族金属间掺杂有可能在很大程度上影响、改变化合物的几何构型和电子结构, 进而影响其物理化学性质.

  一般而言, 催化剂的性能与催化剂表面的活性位状况有着密切的关系^[34].在这类过渡金属硫化物催化材料的活性位研究方面, 前人做了许多工作. Topse等^[35]提出MoS₂表面的边缘位置对HDS催化过程有着不可忽视的作用.特别是有不少研究指出HDS活性中心与催化剂表面的配位不饱和位 (CUS) 密切相关, 但也有研究指出在不含配位不饱和位 (CUS) 的催化剂表面也具有相应的催化活性^{[30, 36~40]}.另有研究表明铌硫化物在HDT反应中所表现的高活性与其表面的S₂^2-基团以及Nb^Ⅳ-Nb^Ⅳ阳离子对有关^[26].尽管前人已对催化活性位的研究取得了不少进展, 但目前人们依然对活性位的精细结构等存在着争议^{[16, 28]}.

  气相团簇作为连接宏观与微观世界的桥梁, 常被用作研究块材体系的理论分子模型.早在20世纪末, 黄建全、卢嘉锡等^[41]科学家就提出了[Mo₃S₄]⁴⁺簇骼中Mo₃S₃簇环具有类芳香性本质.随后厦门大学的黄荣彬等^[42]通过质谱分析实验认为[Nb₃S₄]⁺簇合物也具有类芳香性的Nb₃S₃簇环.值得注意的是, 由于铌 (4d⁴5s¹) 与钼 (4d⁵5s¹) 是同一周期互为邻族的过渡金属元素, 那么[Nb₃S₄]⁺与[Mo₃S₄]⁴⁺就具有相同的价电子数目.此外, Gemming等^[43~46]借助实验光电子能谱 (PES) 和理论计算模拟相结合的手段, 对一系列一核到多核钼硫簇的结构和性质进行了研究, 提供了部分钼硫簇的实验光电子能谱数据.中科院山西煤炭化学研究所的焦海军研究员与其合作者们^[47]指出Mo₃S₉簇具有较小的HOMO-LUMO能隙值, 既可以作为Lewis酸也可以作为Lewis碱, 并提出该团簇可以作为研究无定形MoS₃材料的理论模型.此外, Bertram等^[48]还利用紫外光电子能谱实验结合密度泛函理论计算方法对幻数团簇M₄X₆ (M＝W, Mo, X＝O, S) 进行研究, 确定了Mo₄S₆的结构, 指出其具有较大的HOMO-LUMO能隙值. Andrews小组^{[49, 50]}结合红外光谱实验与密度泛函理论计算, 研究了一系列单核MS_n (M＝V, Nb, Ta, n＝1~2; M＝Cr, Mo, W, n＝1~3) 团簇体系, 计算了其M－S键的特征振动频率.目前, 人们对铌硫簇的研究还比较有限, 研究多集中在与铌同族的钒的硫化物上^{[51, 52]}.对于掺杂铌钼硫体系, 近年来Saha与Raghavachari^{[53, 54]}报道了二元过渡金属硫簇M₂S_x^-(M＝Mo, W, x＝4~6) 以及三元过渡金属硫簇MoWS₄^-掺杂体系的稳定构型, 并对它们与水分子反应的反应机理进行了研究. Afanasiev等^[55]合成了Nb₂Mo₃S₁₀并对其催化性质进行了表征, 指出该物质在噻吩加氢脱硫反应中的催化活性位于MoS₂和NbS₂之间, 而且比它们都更加稳定. Gaborit等^[56]对不同铌钼掺杂比例的Nb_xMo_1−xS₂催化活性进行了比较, 最终认为当x＝0.4时其催化活性最高, 且掺Nb后其催化活性受H₂S的抑制作用会降低.另外Aray等^[57]的研究也表明MoS₂催化剂表面掺Nb有助于提高其热力学稳定性. Ivanovskaya等^{[58, 59]}对掺杂Nb后MoS₂纳米管的稳定性、结构与电子性质进行了研究, 表明掺杂Nb不仅有利于提高MoS₂纳米管的稳定性, 而且掺杂后使纳米管具有金属特性. Deepak等^[60]实验合成了类富勒烯纳米颗粒Nb_xMo_1−xS₂, 并对其进行实验表征, 发现其在低温下具有单电子隧道效应.尽管目前人们对铌钼硫体系的研究做了大量工作, 但掺杂体系的理论研究仍比较缺乏, 因此, 我们希望通过对铌钼硫团簇NbMoS_n^-/0(n＝3~7) 掺杂体系的研究, 分析掺杂、调节硫含量、改变团簇所带电荷等手段对团簇几何构型、电子结构、化学成键等性质的影响, 探索其特征规律与催化活性间的联系, 帮助我们从分子层面加深对这类铌钼硫掺杂体系的了解, 有助于我们进一步解释发生在这类材料表面的各种理化过程, 例如加深对其在加氢脱硫等催化过程中构效关系的理解, 为该类功能材料的性能改进提供较为可靠的理论依据.

  2   计算方法

  本论文的计算工作使用Gaussian 03软件^[61].采用B3LYP杂化密度泛函^[62~64], 先对NbMoS_n^-/0(n＝3~7) 体系的所有原子 (Nb, Mo和S) 使用def2-TZVP赝势及基组 (记作B3LYP/Basis-Ⅰ)^[65~67], 搜索体系势能面, 确定最稳定构型及与其能量相近的异构体.然后, 对上述计算得到的相对能量在0.50 eV以内的结构采用更高水平的赝势及基组进行优化, 即对Nb和Mo原子使用考虑了标量相对论效应的Stuttgart有效核势 (ECP) 及基组^{[68, 69]}, 并在该基组中添加了两个f型和一个g型的极化函数Nb/[ζ(f)＝0.261, 0.970; ζ(g)＝0.536], Mo/[ζ(f)＝0.338, 1.223; ζ(g)＝0.744]^[65], 对S原子采用aug-cc-pVTZ基组^{[70, 71~73]}, 该套赝势及基组在下文中简单记作B3LYP/ Basis-Ⅱ.对于其中能量极其靠近, 与最稳定构型可能存在竞争关系的异构体, 我们采用更高计算精度的耦合簇[CCSD (T)]方法^[74~78](利用Molpro 2010.1软件^[79]) 来进行检验.最终确定了较为可靠的基态结构.计算中各驻点 (stationary point) 的性质是通过计算振动频率来确认.体系各构型的三维分子轨道图由Gauss View 4.1软件^[80]绘制完成.

  由于光电子能谱 (PES) 可作为辨别团簇, 获得团簇电子结构信息的有效工具, 所以在确定NbMoS_n^-/0(n＝3~7) 体系基态构型的基础上, 我们模拟了各阴离子的光电子能谱图, 以期为将来NbMoS_n^-(n＝3~7) 体系光电子谱图的辨析与进一步解释提供数据支持.在模拟光电子能谱过程中所需的垂直电子逸出能 (VDE) 的计算, 是基于广义Koopmans定理 (GKT), 即在阴离子轨道能量本征值基础上加上一个校正项δE＝E₁－E₂－ε_HOMO^[81], 其中E₁和E₂分别代表阴离子基态及其中性团簇在阴离子基态结构下的总能量, ε_HOMO代表阴离子基态结构最高占据轨道 (HOMO) 的本征值.谱图拟合是将计算得到的垂直电子逸出能值以高斯函数展开, 半峰宽为0.10 eV.

  3   结果与讨论

  3.1   优化构型

  在B3LYP/Basis-Ⅱ水平下, 我们发现NbMoS_n^-/0(n＝3~7) 体系的势能面较为平缓, 除发现体系最稳构型外, 还得到若干相对能量与之靠近 (≤0.30 eV) 的异构体 (图 1~5).对这些能量靠近的异构体, 我们采用更高精度的耦合簇[CCSD (T)]单点能计算方法来作进一步确认, 计算结果列于表 1以及附录表S1.总的来说, B3LYP下的结果与CCSD (T) 单点能计算下的结果基本一致, 仅个别相对能量极其靠近的异构体之间发生相对稳定性的翻转.对这些发生翻转的体系, 我们将在文中做进一步讨论.其他在B3LYP/Basis-Ⅰ低基组与B3LYP/Basis-Ⅱ高基组水平下优化得到的结构与其相对能量见于附录 (图S1~S11).

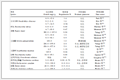  表 1  NbMoS_n^-(n＝3~7) 在不同计算水平下的相对能量及其绝热电子逸出能 (ADE) 与第一点垂直电子逸出能 (VDE_1st) 的结果 Table 1.  Relative energies of selected low-lying isomers of NbMoS_n^-(n＝3~7) with different basis sets, and comparisons with those from the CCSD (T) single-point calculations at the B3LYP geometries together with the corresponding ADE and the first VDE values

  表选项

  导出Excel

  下载全尺寸表图像

  Cluster	B3LYP/Basis-Ⅰa, b	B3LYP/Basis-Ⅱa, c	CCSD (T)-SPa, d	ADE a	VDE1sta
  NbMoS3-(C3v 1A1)	0.00	0.00	0.00	2.54	2.87
  NbMoS3-(Cs 3A″)	0.10	0.18	0.48	2.36	2.65
  NbMoS3-(Cs 1A')	0.15	0.20	0.35	2.35	3.01
  NbMoS4-(Cs 3A″)	0.00	0.00	0.13	2.93	3.33
  NbMoS4-(Cs 5A″)	0.02	0.03	0.24	2.90	3.75
  NbMoS4-(Cs 5A″)	0.04	0.05	0.25	2.88	3.80
  NbMoS4-(C3v 3A1)	0.25	0.24	0.26	2.69	3.07
  NbMoS4-(Cs 3A')	0.26	0.27	0.43	2.66	2.97
  NbMoS4-(Cs 1A')	0.30	0.30	0.00	2.63	2.81
  NbMoS5-(Cs 3A')	0.00	0.00	0.19	3.49	3.82
  NbMoS5-(Cs 1A')	0.05	0.06	0.00	3.43	3.68
  NbMoS5-(Cs 3A″)	0.21	0.18	0.26	3.31	3.73
  NbMoS5-(Cs 1A')	0.22	0.23	0.34	3.25	3.95
  NbMoS5-(Cs 3A')	0.23	0.24	0.46	3.24	3.84
  NbMoS6-(Cs 1A')	0.00	0.00	0.00	4.27	4.69
  NbMoS7-(C1 1A)	0.00	0.00	0.00	4.13	4.46
  NbMoS7-(C1 1A)	0.13	0.15	0.11	3.98	4.48
  aAll energies are in eV; b B3LYP/Basis-Ⅰ; cB3LYP/Basis-Ⅱ; dCCSD (T) single-point calculations at the B3LYP/Basis-Ⅱ geometries.

  表 1  NbMoS_n^-(n＝3~7) 在不同计算水平下的相对能量及其绝热电子逸出能 (ADE) 与第一点垂直电子逸出能 (VDE_1st) 的结果
  Table 1.  Relative energies of selected low-lying isomers of NbMoS_n^-(n＝3~7) with different basis sets, and comparisons with those from the CCSD (T) single-point calculations at the B3LYP geometries together with the corresponding ADE and the first VDE values

  3.2   光电子能谱模拟与分子轨道分析

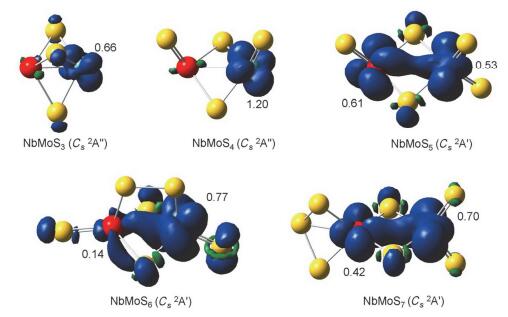
  本工作计算了NbMoS_n^-(n＝3~7) 阴离子基态及与之相对能量靠近的异构体的垂直电子逸出能 (VDEs), 采用广义Koopmans定理 (GKT) 加修正项的方法, 模拟各个S₂^2-体系的阴离子光电子能谱 (PES), 模拟的光电子谱图如图 6所示; 各NbMoS_n^-体系对应第一点VDE值 (VDE_1st) 见表 1; 各基态构型的自旋电子密度图见图 7; 各NbMoS_n^-/0(n＝3~7) 体系有关的价层分子轨道见图 8~12.这些图中黄色球表示硫原子, 红色球表示铌原子, 天蓝色球表示钼原子.

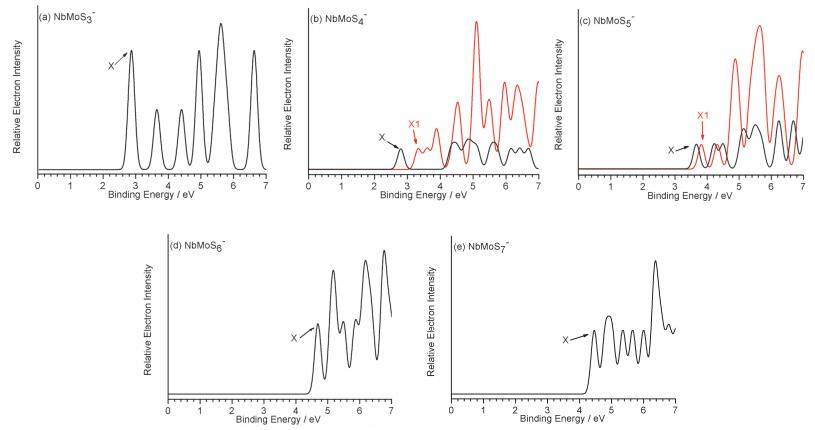  图 6  模拟NbMoS_n^-(n＝3~7) 阴离子基态及其竞争结构的光电子能谱图 (黑线:一重态; 红线:三重态) Figure 6.  Simulated photoelectron spectra from the ground states and selected low-lying isomers of NbMoS_n^-(n＝3~7) clusters at the B3LYP//Basis-Ⅱ level of theory. (Singlets show in black lines and triplets in red lines) The simulations are done by fitting the distribution of calculated VDEs with unit-area Gaussian functions of 0.1 eV width

  图选项

  下载全尺寸图像

  下载幻灯片

  图 7  NbMoS_n (n＝3~7) 基态构型的电子自旋密度 (|e|) 示意图 (蓝色区域代表单电子的分布, 黑色数值代表自旋密度值) Figure 7.  Electron spin density (in |e|) for the ground states of NbMoS_n (n＝3~7) clusters

  图选项

  下载全尺寸图像

  下载幻灯片

  图 8  NbMoS₃^-/0基态的价层分子轨道图 Figure 8.  Valence molecular orbitals for the ground states of (a) NbMoS₃ and (b) NbMoS₃^-

  图选项

  下载全尺寸图像

  下载幻灯片

  图 9  NbMoS₄^-/0基态及其竞争结构的价层分子轨道图 Figure 9.  Valence molecular orbitals for the ground states and selected low-lying isomer of NbMoS₄ and NbMoS₄^-

  图选项

  下载全尺寸图像

  下载幻灯片

  图 10  NbMoS₅^-/0基态及其竞争结构的价层分子轨道图 Figure 10.  Valence molecular orbitals for the ground states and selected low-lying isomer of NbMoS₅ and NbMoS₅^-

  图选项

  下载全尺寸图像

  下载幻灯片

  图 11  基态NbMoS₅^-/0的价层分子轨道图 Figure 11.  Valence molecular orbitals for the ground states of (a) NbMoS₆ and (b) NbMoS₆^-

  图选项

  下载全尺寸图像

  下载幻灯片

  图 12  基态NbMoS₇^-/0的价层分子轨道图 Figure 12.  Valence molecular orbitals for the ground states of (a) NbMoS₇ and (b) NbMoS₇^-

  图选项

  下载全尺寸图像

  下载幻灯片

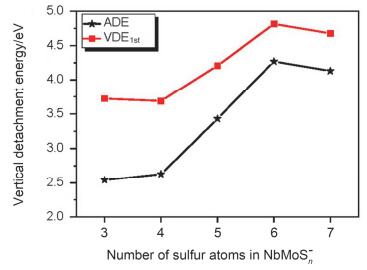
  3.3   NbMoS_n^-(n＝3~7) 的VDE_1st与ADE随硫含量的变化趋势

  图 13是NbMoS_n^-(n＝3~7) 基态的VDE_1st与ADE随硫含量变化而变化的趋势图, 我们能看到明显的两个趋势:其一, VDE_1st与ADE随硫含量增加的变化趋势是基本一致的; 其二, 随着硫含量的增加对应的VDE_1st与ADE呈现先增后降的趋势, 即当n＝6时VDE_1st与ADE达到了最大值 (ADE＝4.27 eV; VDE_1st＝4.69 eV), 而从NbMoS₆^-到NbMoS₇^-, 对应的VDE_1st与ADE值开始降低 (即先增后降).出现这样趋势的原因可结合前面的各体系价层分子轨道 (图 8~12) 分析得知:当n≤6时随着硫含量n增加, 金属Mo (4d⁵5s¹) 和Nb (4d⁴5s¹) 原子上的价电子因要与硫原子成键而逐渐减少, 金属原子的氧化态逐渐增大, 相应地体系第一点VDE (VDE_1st) 和ADE值均呈现逐渐增大的趋势; 在n＝6时铌和钼达到它们的最高氧化态+5和+6, 此时VDE_1st和ADE值也达到最大值.在此过程中较为特别的是, 从NbMoS₃^-到NbMoS₄^-的VDE_1st和ADE值有略微下降, 其原因可以理解为体系由三桥结构变为双桥结构, 这时金属-金属间键长增长 (2.062 →2.487 ), 金属-金属间成键变弱, 那么打掉该成键轨道上的4d电子所需能量减少, 对应的VDE_1st和ADE值也相应变小; 当n＝7时, VDE_1st和ADE值的下降可理解为相应的电子是从NbMoS₇^-上的S₂基团π^*反键轨道上被打掉, 从反键轨道上打掉电子所需能量较少.

  图 13  基态阴离子NbMoS_n^-(n＝3~7) VDE_1st与ADE随硫含量的变化趋势图 Figure 13.  The calculated VDE_1st and ADE of NbMoS_n^-(n＝3~7) as a function of S content (n)

  图选项

  下载全尺寸图像

  下载幻灯片

  3.4   NbMoS_n^-/0(n＝3~7) 的结构演化和顺序硫化

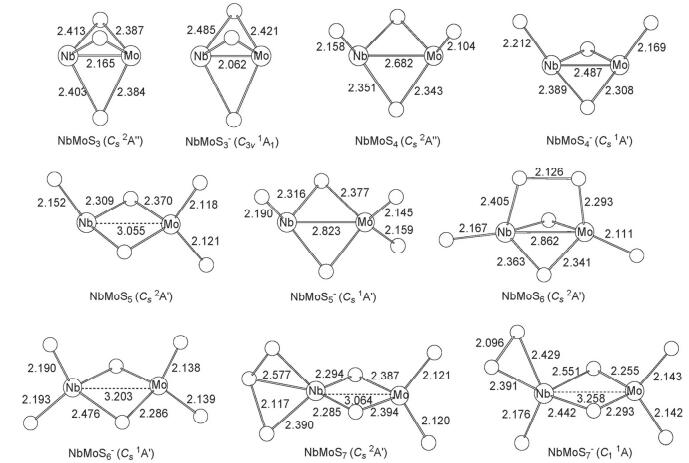
  NbMoS_n^-/0(n＝3~7) 的基态构型如图 14所示.对于中性NbMoS_n (n＝3~7) 而言, 可以认为NbMoS₃的基态构型是在NbMoS₂四元环的基础上先增加一个桥硫原子得到; 而NbMoS₄基态构型是在NbMoS₂四元环基础上增加两个端硫原子, 且这两个端硫原子分别加到两种金属原子上得到; 在NbMoS₄基态构型基础上, 再继续增加一个硫原子, 由于钼原子比铌原子剩余的4d价电子数更多, 所以新添的硫原子以端硫形式加到金属钼原子上, 得到NbMoS₅基态构型; 继续增加一个硫原子, 新添的硫原子加到还剩余一个单电子的铌原子上形成硫自由基, 硫自由基再与钼上的一个端硫原子形成桥连的S₂基团, 得到NbMoS₆基态构型; 而NbMoS₇可以认为是在NbMoS₅结构基础上, 于铌端新增一个S₂基团, 形成S₂^-自由基, 然后该S₂^-自由基与铌上的端硫进一步形成S₃基团.

  图 14  在B3LYP/Basis-Ⅱ水平下得到的基态NbMoS_n^-/0(n＝3~7) 构型 Figure 14.  Optimized ground states for NbMoS_n^-/0(n＝3~7) clusters at the B3LYP/Basis-Ⅱ level of theory

  图选项

  下载全尺寸图像

  下载幻灯片

  相应的NbMoS_n^-(n＝3~7) 阴离子基态也有类似的结构演化规律, 在硫含量n＜6时, 阴离子基态结构与中性基态构型基本类似.当硫含量n＝5时, 由于铌原子上仍富余两个价电子, 新增的硫原子加到铌原子上形成端硫, 得到NbMoS₆^-的阴离子基态结构; 对于富硫类型NbMoS₇^-阴离子, 由于铌和钼上已无多余的价电子, 所以新增的硫原子将加到铌的一个端硫原子上, 形成S₂基团.

  3.5   NbMoS_n^-/0(n＝3~7) 的相对稳定性

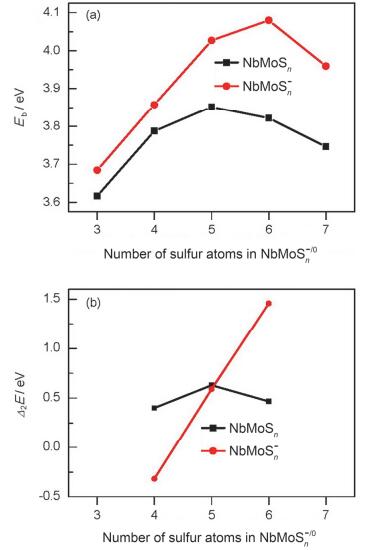
  为了进一步比较该系列团簇在硫含量改变情况下的相对稳定性, 我们分别计算了各基态结构的平均结合能 (E_b) 与能量二阶差分 (△₂E) 值.我们所采用的计算公式如下^{[82, 83]}:

  图 15展示了NbMoS_n^-/0(n＝3~7) 团簇平均结合能 (E_b) 和能量二阶差分 (△₂E) 值随硫含量n的变化关系曲线.从图中可以看出, 不管是平均结合能 (E_b) 的关系曲线, 还是能量二阶差分 (△₂E) 的关系曲线, 其趋势基本一致.在中性NbMoS_n团簇中, 以NbMoS₅的E_b和△₂E值最大, 表明它与其他团簇相比具有更高的稳定性; 而阴离子NbMoS_n^-簇中, NbMoS₆^-的E_b和△₂E值最大, 说明它比其它相邻的团簇更加稳定.

  图 15  NbMoS_n^-/0(n＝3~7) 团簇的平均结合能E_b与能量二阶差分△₂E随硫含量的变化趋势图 Figure 15.  The averaged binding energy (E_b) and second-order energy difference (△₂E) of NbMoS_n^-/0(n＝3~7) as a function of S content (n)

  图选项

  下载全尺寸图像

  下载幻灯片

  3.6   H₂在NbMoS_n^-/0(n＝3~7) 簇合物上的还原反应

  Afanasiev等^[84~86]研究发现MoS₂催化剂边缘位上的S₂^2-对催化加氢脱硫 (HDS) 反应活性有着重要的影响, 如MoS₂催化剂常在高温H₂/H₂S气氛中使用, S₂^2-基团能促进H₂解离成活性氢原子^[87].此外, 铌硫化物也被报道在HDS等反应中表现出了优异的催化性能^[88].因此铌钼掺杂的双金属硫化物在HDS反应中能否引起催化性能的提高成为我们感兴趣的内容.为此, 我们设计了如下的反应 (反应4), 来评估掺杂后铌钼硫化物团簇与H₂反应, 最终以H₂S形式脱去一个S原子的反应驱动力 (－ΔG) 大小, ΔG的大小通过方程5进行计算得到:

  反应4的∆G结果列于表 2中.根据计算结果发现, 对于中性NbMoS_n (n＝3~7), 其与H₂反应的∆G值随硫含量n的增加而降低, 且∆G值均是正值, 这说明中性体系与H₂的反应正向非自发.对于阴离子体系, 发现∆G值随硫含量n的增加出现先增加后减小的趋势, 当n＜7时∆G值均为正值, 当n＝7时∆G值出现负值, 出现负值说明此时反应正向自发.这说明催化剂的预硫化, 使催化剂表面形成端连的S₂^2-基团, 该基团对形成具有催化活性的配位不饱和位 (CUS) 有重要作用.且形成的S₂^2-基团倾向形成于铌原子上, 也说明硫化铌更容易在催化剂表面形成S₂^2-基团并被活化为CUS活性位.我们预计在硫化钼催化剂中掺杂一定比例的铌原子有利于提高MoS₂催化剂的加氢脱硫活性.

  表 2  在B3LYP/Basis-Ⅱ水平下得到的反应 (4) 吉布斯自由能变化值∆G Table 2.  Calculated free energy differences (ΔG) for the proposed reaction (4) at the B3LYP/Basis-Ⅱ level of theory

  表选项

  导出Excel

  下载全尺寸表图像

  n→n－1	∆Gnua, b	∆Gana, b
  4→3	34.92	37.07
  5→4	25.09	43.44
  6→5	9.90	30.96
  7→6	0.77	－3.43
  a∆Gnu and ∆Gan mean ∆G of the neutral and anionic clusters, respectively. bAll energies are in kcal•mol－1.

  表 2  在B3LYP/Basis-Ⅱ水平下得到的反应 (4) 吉布斯自由能变化值∆G
  Table 2.  Calculated free energy differences (ΔG) for the proposed reaction (4) at the B3LYP/Basis-Ⅱ level of theory

  3.7   中性基态NbMoS_n(n＝3~7) 的路易斯酸性

  路易斯酸性强弱, 可以在一定程度上说明其亲电能力的强弱.关于团簇路易斯酸性的大小可通过计算其氟亲和能 (FAs) 得到^{[89, 90]}, 而FA值被定义为反应6焓变的负值 (方程7).

  通过上面关于路易斯酸性的定义, 我们计算得到了NbMoS_n (n＝3~7) 的FA值 (表 3), 通过比较我们发现, FA值随硫含量的增加出现先增加后减小的趋势.从n＝3到n＝5, FA值先增加, 在NbMoS₅时FA值达到最大值5.69 eV.这是由于随硫含量增加, 金属位上的电子逐渐转移到硫原子上参与成键, 金属原子的氧化态逐渐增大.当硫含量继续增大, NbMoS₆和NbMoS₇中开始分别出现S₂^2-基团和S₃^2-基团. F^－和S₂^2-基团均带负电荷, 因此它们间存在较强的静电排斥, 且NbMoS₆和NbMoS₇的空间位阻较大, 因而FA值从n＝6开始下降.此外, 对NbMoS_nF^－(n＝3~7) 最稳构型的搜索, 我们是在NbMoS_n (n＝3~7) 最稳定构型的基础上考虑氟阴离子的不同吸附位置, 包括在Nb位、Mo位、端硫位以及桥硫位上的情况.最终优化得到的结果见于附录图S12.我们发现NbMoS_nF^－ (n＝3~7) 的最稳构型中, F^－倾向直接与金属铌原子成键, 这也说明团簇上的铌原子位有较强的亲电能力.上述数据能为未来改进该类材料的催化活性提供一定的理论依据.

  表 3  方程 (7) 的氟亲和能FA Table 3.  Equation (7) for the values of fluorine affinity (FA)

  表选项

  导出Excel

  下载全尺寸表图像

  Cluster	FAa
  NbMoS3	4.68
  NbMoS4	5.18
  NbMoS5	5.69
  NbMoS6	4.37
  NbMoS7	3.77
  a All energies are in eV.

  表 3  方程 (7) 的氟亲和能FA
  Table 3.  Equation (7) for the values of fluorine affinity (FA)

  3.1.2   NbMoS₄和NbMoS₄^-

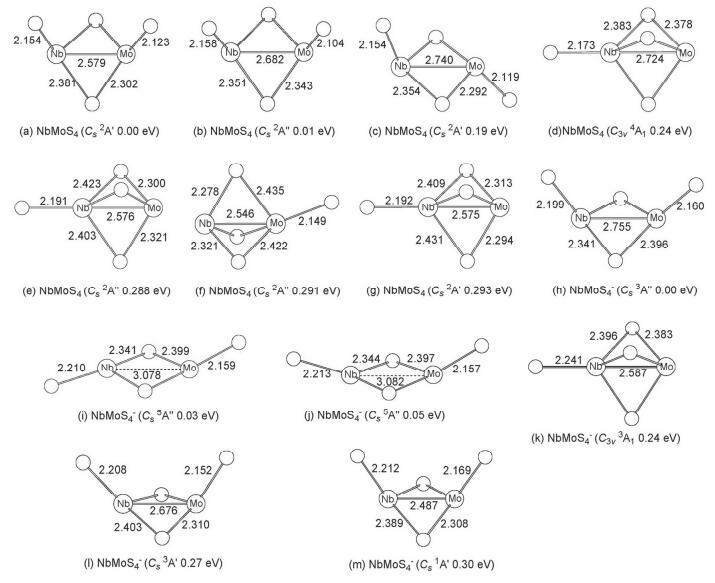
  在NbMoS₃^-/0各种稳定构型的基础上, 我们考虑新增一个硫原子的不同摆放位置.计算结果表明, NbMoS₄^-/0体系的势能面也比较平缓, 除最稳构型外, 也发现多个能量与之靠近的异构体.其中NbMoS₄中性的最稳定构型是一个对称性为C_s (²A') 的二重态结构 (图 2a).该结构含有两个桥硫及两个分别位于铌和钼原子上的端硫原子.我们还得到一个相对能量仅比最稳构型高了0.01 eV的异构体 (C_s ²A″, 图 2b), 这两个异构体不仅结构上类似, 相对能量上也极其接近, 仅在电子态上有所不同 (²A″ vs ²A'), 即使通过CCSD (T) 单点能计算也很难将其完全区分开, 所以在实验中这两种异构体都有可能被观测到.此外, 有一个两桥两端的异构体 (C_s ²A', 图 2c), 该异构体的两个金属原子与两个桥硫原子共同组成一个近平面的NbMoS₂四元环结构, 剩下的两个端硫指向该四元环的不同方向, 其相对能量比最稳构型高了0.19 eV.还有三个三桥一端的异构体 (图 2d~2g), 其相对能量均比最稳构型高了约0.29 eV.

  图 2  在B3LYP/Basis-Ⅱ水平下得到的NbMoS₄^-/0体系最稳构型及与其相对能量靠近的异构体 (键长单位为 ) Figure 2.  Optimized structures for NbMoS₄^-/0 at the B3LYP/Basis-Ⅱ level of theory. The relative energies are in eV and the bond lengths are in angstroms

  图选项

  下载全尺寸图像

  下载幻灯片

  对于NbMoS₄^-阴离子的最稳构型 (图 2h), 其几何结构与中性最稳定结构 (图 2a) 类似, 是一个含有两个桥硫和两个端硫, 对称性为C_s的三重态 (³A″) 结构.另有两个五重态的两桥两端结构 (图 2i和2j), 其相对能量仅比最稳结构分别高了0.03和0.05 eV.此外, 我们还得到了三个相对能量分别为0.24、0.27和0.30 eV的异构体 (图 2k~2m).在这三个异构体中, 有一个与最稳构型结构类似的一重态 (C_s ¹A', 图 2m), 其相对能量虽比最稳构型高了0.30 eV, 但该异构体在CCSD (T) 单点能计算中被认为是最稳构型, 相对能量比B3LYP水平下的最稳构型低了0.13 eV.对这两个稳定性发生翻转的异构体, 我们在B3LYP水平下计算了它们的红外光谱数据, 结果发现B3LYP水平下的最稳构型 (图 2h) 在频率为512.0 cm^－1(s) 和501.65 cm^-1(vs) 处有两个强峰, 分别对应端硫的对称伸缩振动 (ν_s) 和反对称伸缩振动 (ν_as).另外, 在频率431.6 cm^－1(s) 处有一个较强的峰, 在404.1 cm^－1(m) 处有一个中等强度的峰, 分别对应桥硫的反对称伸缩振动 (ν_as) 和对称伸缩振动 (ν_s).而另一个在CCSD (T) 单点能计算中被认为最稳定的结构 (图 3m), 计算发现其在振动频率506.7 cm^－1(vs) 和493.7 cm^－1(vs) 处有两个对应端硫的对称伸缩振动 (ν_s) 和反对称伸缩振动 (ν_as) 的强峰.在461.5 cm^－1(m) 处有一中等强度的峰, 在432.1 cm^－1(vw) 处有一非常弱的峰, 分别对应桥硫的反对称伸缩振动 (ν_as) 和对称伸缩振动 (ν_s). (文中振动强度表示符号: w弱; vw极弱; m中; s强; vs极强)

  图 3  在B3LYP/Basis-Ⅱ水平下得到的NbMoS₅^-/0体系最稳构型及与其相对能量靠近的异构体 (键长单位为 ) Figure 3.  Optimized structures for NbMoS₅^-/0 at the B3LYP/Basis-Ⅱ level of theory. The relative energies are in eV and the bond lengths are in angstroms

  图选项

  下载全尺寸图像

  下载幻灯片

  3.1.3   NbMoS₅和NbMoS₅^-

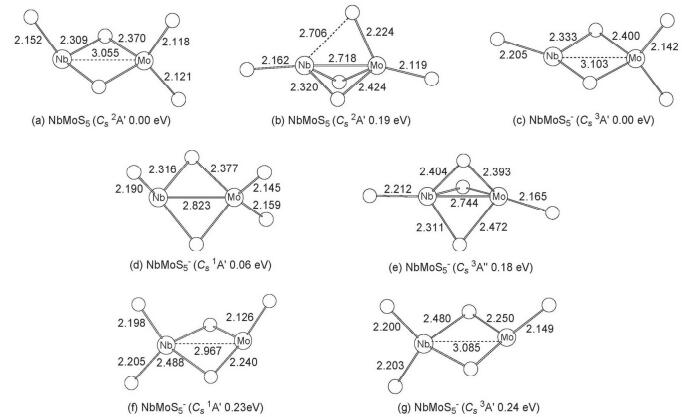
  在NbMoS₄^-/0稳定构型基础上, 我们继续对其添加硫原子.最终优化得到具有两桥三端的中性NbMoS₅最稳定构型 (C_s ²A', 图 3a).其中三个端硫原子, 一个位于铌原子, 两个位于钼原子上.该结构可视作在中性NbMoS₄基础上于钼原子添加一个端硫原子而来.同时我们也得到一个相对能量为0.19 eV具有C_s (²A') 对称性的三桥构型异构体 (图 3b), 该结构中的Nb－Mo金属键长 (2.718 ) 比二桥结构的最稳构型 (3.055 ) 要短得多.这两个异构体在CCSD (T) 单点能计算水平下的结论支持它们在B3LYP计算水平下的结果.

  对NbMoS₅^-阴离子, 其体系势能面较为平缓, 有多个与最稳构型相对能量靠近的异构体.计算结果显示NbMoS₅^-的最稳定构型与中性的最稳定构型类似, 也是一个具有C_s (³A') 对称性的双桥结构 (图 3c), 该结构对应的一重态 (C_s ¹A'), 其相对能量仅比最稳构型高了0.06 eV (图 3d), 该结构中的三个端硫, 一个键连在金属铌上, 两个与金属钼相连.该构型与最稳构型相比, 其金属-金属间距离更短, 距离为2.823 .如果双桥结构的NbMoS₅^-异构体中, 剩下的三个端硫原子有两个位于铌, 一个位于钼上, 则其一重态和三重态的相对能量要比最稳构型分别高了0.23和0.24 eV (图 3f和3g).此外, 我们还找到一个三桥结构的异构体 (图 3e), 其相对能量比最稳构型高了0.18 eV.对这些异构体我们都采用CCSD (T) 方法进行单点能计算 (表 1), 其结果与B3LYP水平下的结果基本一致, 仅相对能量最为靠近的两个异构体 (图 3c和3d) 的稳定性发生颠倒, 即认为一重态的双桥结构异构体 (图 3d) 比其三重态异构体 (图 3c) 更加稳定.对于这两个NbMoS₅^-阴离子相对能量发生翻转的异构体, 我们同样对其红外光谱进行了模拟计算, 结果发现三重态的异构体 (图 4c) 在536.3 cm^－1(s) 处有一强峰, 对应端硫的反对称伸缩振动 (ν_as).在520.4 cm^－1(vw) 处有一非常弱的峰, 在505.2 cm^－1(vs) 处有一非常强的峰, 对应端硫的对称伸缩振动 (ν_s).其中在520.4 cm^－1(vw) 处的峰由于其峰强非常弱, 所以在实验中可能会淹没于两旁的两个强峰中, 成为鉴别该异构体的一个明显指纹特征.在436.7 cm^－1(m) 和402.6 cm^－1(w) 处分别有一中等强度和较弱的峰, 对应桥硫的反对称伸缩振动 (ν_as) 和对称伸缩振动 (ν_s).对于另一个单重态异构体 (图 4d), 其红外光谱模拟计算发现:在530.8 cm^－1(s) 处有一强峰, 对应端硫的反对称伸缩振动 (ν_as).在515.7 cm^－1(m) 和501.4 cm^－1(vs) 处分别有一个中等强度和非常强的峰, 对应端硫的对称伸缩振动 (ν_s).在447.1 cm^－1 (m) 和419.8 cm^－1 (w) 处分别有一中等强度和较弱的峰, 对应桥硫的反对称伸缩振动 (ν_as) 和对称伸缩振动 (ν_s).上述谱峰位置与Andew小组^{[44, 45]}对NbS_x、MoS_x团簇的矩阵红外光谱实验中, 所报道的端硫振动频率的理论值与实验值基本相符 (NbS₂端硫的ν_s和ν_as理论值分别为536.9 cm^－1和534.8 cm^－1, 其实验值分别为525.1 cm^－1和531.0 cm^－1; MoS₂端硫的ν_s和ν_as理论值分别523.8 cm^－1和534.8 cm^－1, ν_as实验值为535.7 cm^－1).

  图 4  在B3LYP/Basis-Ⅱ水平下得到的NbMoS₆^-/0体系最稳构型及与其相对能量靠近的异构体 (键长单位为 ) Figure 4.  Optimized structures for NbMoS₆^-/0 at the B3LYP/Basis-Ⅱ level of theory. The relative energies are in eV and the bond lengths are in angstroms

  图选项

  下载全尺寸图像

  下载幻灯片

  3.1.1   NbMoS₃和NbMoS₃^-

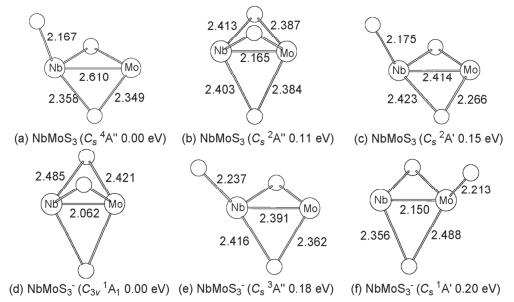
  对NbMoS₃^-/0体系, 我们设计了各种可能的初始结构, 包括两金属原子间键连一个桥硫、两个桥硫以及三个桥硫的情况, 对每种初始结构我们还考虑了它们在不同自旋多重度下的情况.计算结果表明, 在B3LYP水平下得到的中性NbMoS₃最稳定构型是一个具有C_s对称性的四重态 (⁴A″) 结构 (图 1a), 该结构含有两个桥硫原子, 剩下的一个硫原子以端硫形式与铌原子相连.除该最稳构型外, 我们还找到一个与之能量靠近的竞争异构体, 该异构体相对能量仅比最稳构型高了0.11 eV, 它是一个具有C_s (²A″) 对称性 (图 1b) 且含有三个桥硫的结构.此外, 与最稳定结构形似的二重态异构体 (C_s ²A', 图 1c), 其相对能量比最稳构型高了0.15 eV, 它的Nb－Mo金属键长略有缩短变为2.414 .我们对这三个竞争的异构体采用更高精度的耦合簇[CCSD (T)]方法进行单点能计算, 结果显示两桥一端的二重态异构体 (图 1c) 其相对能量仍然较高, 但原先在B3LYP水平下次稳的三桥构型 (图 1b) 在CCSD (T) 单点能计算水平下却要比两桥一端的四重态 (图 1a) 能量稍低, 低了0.09 eV.在现有的计算水平下, 我们认为该三桥的C_s (²A″) 构型 (图 1b) 为中性NbMoS₃的基态结构.

  图 1  在B3LYP/Basis-Ⅱ水平下得到的NbMoS₃^-/0体系最稳构型及与其相对能量靠近的异构体 (键长单位为 ) Figure 1.  Optimized structures for NbMoS₃^-/0 at the B3LYP/Basis-Ⅱ level of theory. The relative energies are in eV and the bond lengths are in angstroms

  图选项

  下载全尺寸图像

  下载幻灯片

  对于NbMoS₃^-阴离子, 其最稳定构型与中性基态结构 (图 1b) 相类似, 也是一个含有三个桥硫原子的闭壳层高对称性结构 (C_3v ¹A₁, 图 1d).对于端硫键连在铌原子上的二桥结构 (C_s ³A″, 图 1e), 其相对能量比最稳构型高了0.18 eV, 而端硫位于钼原子上的二桥结构 (C_s ¹A', 图 1f), 其相对能量比最稳构型高了0.20 eV.对这些异构体我们也采用了CCSD (T) 方法进行单点能计算, 结果与B3LYP下的结论相一致.

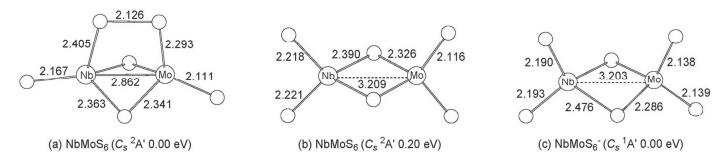
  3.1.4   NbMoS₆和NbMoS₆^-

  对中性NbMoS₆的计算结果发现, 其最稳构型为一个具有C_s(²A') 对称性的二重态 (图 4a), 它含有两个端硫、两个桥硫和一个桥连的二硫 (S₂) 基团, 该二硫 (S₂) 基团中S－S键键长为2.126 ,与相同基组水平下计算得到的游离态的S₂^2-(¹Σ_g⁺) 的键长 (2.180 ) 相近, 可以

  看作由S₂^2-基团与NbMoS₄²⁺相结合得到.此外, 我们还得到一个二桥四端结构的异构体 (C_s ²A', 图 4b), 其相对能量为0.20 eV.这两个异构体在CCSD (T) 水平下计算单点能, 其结果与B3LYP水平下的结果一致, 支持含S₂^-2基团的异构体 (图 4a) 为中性NbMoS₆的基态.

  对于NbMoS₆^-阴离子, 计算结果显示最稳构型为闭壳层的两桥四端构型 (C_s¹A', 图 4c), 该结构与中性基态的构型差异较大.可能是由于多余的一个电子加入S₂^2-基团中, 导致该基团断裂为两个端硫的缘故.

  3.1.5   NbMoS₇和NbMoS₇^-

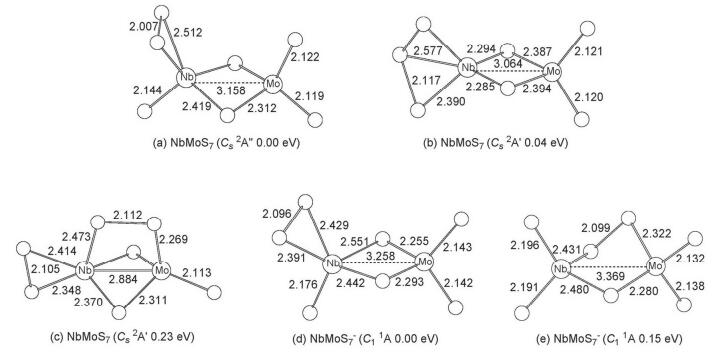
  对富硫类型的NbMoS₇^-/0体系, 计算结果显示, 中性NbMoS₇的最稳构型是一个含两个桥硫、三个端硫和一个端连在金属铌原子位上的二硫 (S₂) 基团的结构 (图 5a), 通过自旋密度分析得知 (S₂) 基团上分布有一个单电子, 且S－S键长 (2.007 ) 与相同基组水平下计算得到的游离态s₂^- (²Π_g) 的键长 (2.029 ) 相接近, 因此可以看作以 (s₂^-) 基团与NbMoS₅⁺单元相结合得到.同时我们还得到了一个相对能量为0.04 eV, 对称性为C_s (²A″) 的二重态异构体 (图 5b), 该异构体含有一个位于金属铌原子上的端位S₃基团, 其S－S键长为2.117 .此外我们还找到一个相对能量为0.23 eV的构型 (图 5c), 该构型含有两种不同类型的S₂基团, 即一个桥连的S₂^2-基团.对这些异构体, 我们亦通过CCSD (T) 单点能计算的方法来确认其相对稳定性, 结果发现B3LYP方法下的最稳结构 (图 5a) 与次稳构型 (图 5b) 的相对能量仍非常靠近, 仅相差0.06 eV, 其中含S₃基团的次稳构型 (图 5b) 相对能量略低, 理论模拟与实验谱图的对照有利于进一步辨别哪种构型是真正的基态结构.

  图 5  在B3LYP/Basis-Ⅱ水平下得到的NbMoS₇^-/0体系基态和与其相对能量靠近的异构体 (键长单位为 ) Figure 5.  Optimized structures for NbMoS₇^-/0 at the B3LYP/Basis-Ⅱ level of theory. The relative energies are in eV and the bond lengths are in angstroms

  图选项

  下载全尺寸图像

  下载幻灯片

  计算结果指出NbMoS₇^-阴离子的最稳定构型是一个具有C₁对称性的含有两个桥硫三个端硫和一个端连在铌原子上的S₂基团的结构 (图 5d).该结构中的S₂基团的S－S键长为2.096 ,与相同水平下计算得到的游离态S₂^2-的键长 (2.180 ) 接近, 因此也可以看作是以S₂^2-基团与NbMoS₅⁺相结合得到, 该构型与中性NbMoS₇在B3LYP水平下的最稳定构型类似.此外我们也得到了一个相对能量为0.15 eV含有四端两桥 (两桥中一个为桥连的S₂基团) 的构型 (图 5e).这两个异构体我们也采用更高精度的耦合簇[CCSD (T)]方法计算单点能, 得到的结果与B3LYP水平下的结果相一致.

  3.2.2   NbMoS₄和NbMoS₄^-

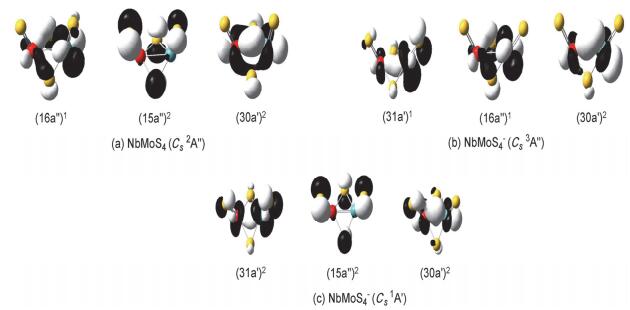
  中性基态NbMoS₄ (C_s ²A″) 的价电子组态为…(14a″)²(29a')²(30a')²(15a″)²(16a″)¹.其中最高单占据分子轨道SOMO (16a″)¹主要为两金属原子上的4d轨道成分; (15a″)²主要是端硫和桥硫上的3p轨道成分; 另外 (30a')²轨道主要是金属铌与金属钼以“头碰头”形成的4d-σ成键轨道成分.基态阴离子NbMoS₄^-(C_s¹A') 与中性基态构型类似, 也为两桥两端的结构.其价电子组态是…(14a″)²(29a')²(30a')²(15a″)²(31a')²(图 9c).其中最外层HOMO (31a')²主要为金属铌和钼上的4d轨道成分.打掉该双占据轨道 (HOMO) 上的一个电子会产生谱图的第一点VDE值, 即2.81 eV (表 1), 对应谱图的第一个谱峰 (对应图 6b黑线上X位置).另外基态阴离子存在一个能量靠近且构型相近的三重态结构 (C_s ³A″), 其价电子组态是…(29a')²(15a″)²(30a')²(16a″)¹(31a')¹(图 9b).其SOMO (31a')¹轨道主要为金属间“头碰头”形成的4d-σ成键轨道; 次外层的 (16a″)¹对应中性的单占据轨道.另外我们也模拟了其光电子能谱 (对应图 6b红线上X1位置), 对应的第一点VDE值为3.33 eV (表 1).

  3.2.1   NbMoS₃和NbMoS₃^-

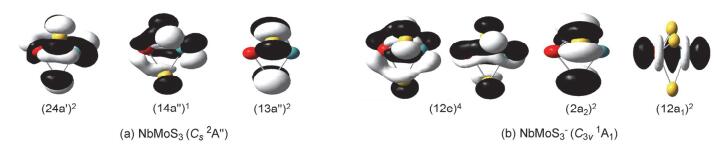
  中性NbMoS₃和阴离子NbMoS₃^-的价层分子轨道如 (图 8) 所示.中性基态NbMoS₃ (C_s ²A″) 的价电子组态为…(12a″)²(23a')²(13a″)²(14a″)¹(24a')².其HOMO轨道 (24a')²主要是两个金属间的4d-π成键轨道; 次外层是一个单占轨道 (14a″)¹, 主要也是两个金属间的4d-π成键轨道.阴离子基态NbMoS₃^-(C_3v ¹A₁) 可认为是在中性NbMoS₃基态上增加一个电子得到, 其价电子组态是…(11e)⁴(12a₁)²(2a₂)²(12e)⁴.最高占据分子轨道HOMO的 (12e)⁴为全满的简并轨道, 主要是金属铌钼间的4d-π成键轨道; 其次外层 (2a₂)²主要成分为三个桥硫原子的3p非键轨道; (12a₁)²是金属间以“头碰头”形式形成4d-σ成键轨道.打掉最外层 (12e)⁴简并轨道上的一个电子得到第一点VDE值2.87 eV (表 1), 对应模拟光电子谱图中第一个谱峰X的位置 (图 6a).

  3.2.3   NbMoS₅和NbMoS₅^-

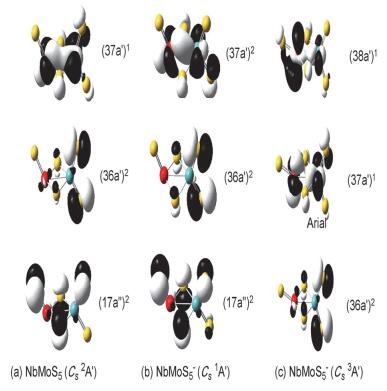
  中性基态NbMoS₅(C_s ²A') 的价电子组态为…(35a')²-(16a″)²(17a″)²(36a')²(37a')¹.其中SOMO (37a')¹轨道的主要成分是金属铌钼之间的4d轨道; (36a')²及以下的分子轨道主要成分为端硫和桥硫的3p轨道成分.通过自旋密度图能看到单电子主要位于金属铌和钼上.阴离子基态NbMoS₅^-(C_s ¹A') 可认为是在中性NbMoS₅基态的SOMO (37a')¹添加一个电子而来, 其价电子组态是…(16a″)²(17a″)²(36a')²(37a')²(图 10b).打掉阴离子NbMoS₅^-基态HOMO上的一个电子会产生第一个谱峰 (对应图 6c黑线上X位置), 对应的VDE值是3.68 eV (表 1).另外基态阴离子存在一个能量靠近且构型相近的三重态结构 (C_s³A″), 其价电子组态是…(35a')²(17a″)²-(36a')²(37a')¹(38a')¹(图 10c).其SOMO (38a')¹轨道主要为金属铌和钼上两种类型的4d轨道形成较弱的4d-σ成键; 次外层的 (37a')¹单占据轨道金属间形成非键.与此同时我们也模拟了三重态异构体 (C_s ³A') 的光电子能谱 (图 6c红线上X1位置), 其第一点VDE计算值为3.82 eV (表 1).

  3.2.5   NbMoS₇和NbMoS₇^-

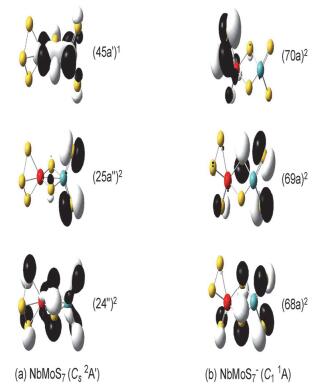
  中性基态NbMoS₇ (C_s ²A') 的价电子组态…(43a')²(44a')²(24a″)²(25a″)²(45a')¹.其SOMO轨道 (45a')¹主要成分为金属铌和钼间的4d-σ成键轨道.自旋密度图 (图 7) 看到单电子主要位于金属铌和钼上.基态阴离子NbMoS₇^-(C₁ ¹A) 的价电子组态是…(67a)²(68a)²-(69a)²(70a)². HOMO轨道 (70a)²主要成分为NbMoS₇^-基团上两个3p轨道形成的π^*反键轨道; 而次外层的 (69a)²轨道主要为端硫和桥硫上的3p轨道成分.打掉基态阴离子NbMoS₇^-的HOMO轨道上的一个电子会产生第一个谱峰 (对应图 6e黑线上X位置), 对应的VDE值是4.46 eV (表 1).

  3.2.4   NbMoS₆和NbMoS₆^-

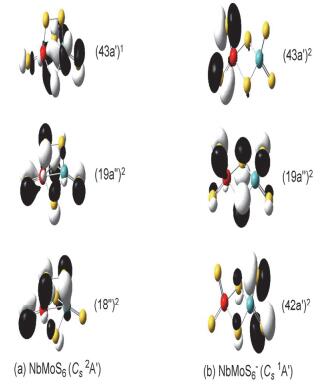
  中性基态NbMoS₆ (C_s ²A') 的价电子组态是…(17a″)²(42a')²(18a″)²(19a″)²(43a')¹.其中SOMO (43a')¹主要成分是由金属钼和铌上4d轨道以“头碰头”形式形成的σ成键轨道; 次外层轨道 (19a″)²主要为桥位硫的S₂基团、桥硫和桥端硫上含明显的3p轨道; (18a″)²主要是位于NbMoS₆^-基团上的两个硫存在强烈的π^*反键轨道.自旋密度图 (图 7) 能看到单电子主要位于金属钼上.阴离子基态NbMoS₆^-(C_s ¹A') 的价电子组态是…(18a″)²-(42a')²(19a″)²(43a')². HOMO (43a')²及以下分子轨道3p成分较为明显, 即端硫和桥硫上的3p轨道.打掉基态阴离子NbMoS₅^-HOMO轨道上的一个电子会产生第一个谱峰 (对应图 6d黑线上X位置), 对应的VDE值是4.69 eV (表 1).

  4   结论

  本论文采用密度泛函 (DFT) 与耦合簇[CCSD (T)]方法对一系列掺杂类型的二核NbMoS_n^-/0(n＝3~7) 团簇体系进行广泛的势能面搜索, 寻找体系最稳定的几何构型, 并对其在几何、电子结构与化学成键等方面所表现出来的性质规律进行研究.在确定NbMoS_n^-阴离子基态结构的基础上, 我们采用广义Koopmans定理计算出电子垂直逸出能 (VDE), 并模拟了各阴离子的光电子能谱, 结合对分子轨道的分析进一步讨论该铌钼硫掺杂团簇体系在顺序硫化过程中的演变规律.结果表明: NbMoS_n^-/0(n＝3~7) 基态可视为在NbMoS₂四元环基础上逐渐加硫演变而来, 各种硫配体出现的先后顺序如下:在金属Nb和金属Mo分别达到其最高氧化态+5和+6之前, S以桥位或端位形式出现, 当Nb和Mo达到最高氧化态后, Nb和Mo原子上没有多余的价电子用来成键, 因此开始出现桥连或端连的S₂基团, 硫含量继续增大, 最后出现端连的S₃基团; 我们还对NbMoS_n^-/0团簇体系与H₂反应的驱动力进行计算, 结果发现S₂^2-基团对形成配位不饱和位 (CUS) 有重要作用.因而硫化钼中掺杂适量的Nb以及在催化剂制备时充分预硫化处理, 将对S₂^2-基团的形成有利, 上述措施有可能提高催化剂CUS活性位的浓度, 进而提高其催化活性.此外, 具有配位不饱和位的NbMoS₅具有最大的路易斯酸性, 有较好的亲电能力.上述结果为探索新的掺杂类型过渡金属硫化物催化剂提供了一定的理论依据和启示.

• 1. [1]

     史建平, 马冬林, 张艳锋, 刘忠范, 化学学报, 2015, 73, 877. doi: 10.6023/A15030157Shi, J. P.; Ma, D. L.; Zhang, Y. F.; Liu, Z. F. Acta Chim. Sinica 2015, 73, 877. doi: 10.6023/A15030157

  2. [2]

     Transition Metal Sulfur Chemistry:Biological and Industrial Significance, Eds.:Stiefel, E. I.; Matsumoto, K., American Chemical Society, Washington, 1996.

  3. [3]

     Lee, S. C.; Li, J.; Mitchell, J. C.; Holm, R. H. Inorg. Chem. 1992, 31, 4333. doi: 10.1021/ic00047a021

  4. [4]

     Nasretdinova, V.; Zaitsev-Zotov, S. Physica B 2012, 407, 1874. doi: 10.1016/j.physb.2012.01.052

  5. [5]

     Wang, Q.; Zhao, J.; Wang, X. F. J. Phys. Chem. A 2015, 119, 2244. doi: 10.1021/jp5054106

  6. [6]

     Pettarin, V.; Churruca, M. J.; Felhos, D.; Karger-Kocsis, J.; Frontini, P. M. Wear 2010, 269, 31. doi: 10.1016/j.wear.2010.03.006

  7. [7]

     Basharina, K. Y.; Terekhin, D. V.; Kuz'mina, G. N.; Bordubanova, A. E.; Ezhov, G. A.; Parenago, O. P. Petrol. Chem. 2009, 49, 339. doi: 10.1134/S0965544109040148

  8. [8]

     Chhowalla, M.; Amaratunga, G. A. J. Nature (London) 2000, 407, 164. doi: 10.1038/35025020

  9. [9]

     Ye, L. N.; Wu, C. Z.; Guo, W.; Xie, Y. Chem. Commun. 2006, 45, 4738.

  10. [10]

      Walter, M. G.; Warren, E. L.; McKone, J. R.; Boettcher, S. W.; Mi, Q.; Santori, E. A.; Lewis, N. S. Chem. Rev. 2010, 110, 6446. doi: 10.1021/cr1002326

  11. [11]

      Jaramillo, T. F.; Jørgensen, K. P.; Bonde, J.; Nielsen, J. H.; Horch, S.; Chorkendorff, I. Science 2007, 317, 100. doi: 10.1126/science.1141483

  12. [12]

      田野, 何俣, 尚静, 朱永法, 化学学报, 2004, 62, 1807. http://sioc-journal.cn/Jwk_hxxb/CN/abstract/abstract344143.shtmlTian, Y.; He, Y.; Shang, J.; Zhu, Y. F. Acta Chim. Sinica 2004, 62, 1807. http://sioc-journal.cn/Jwk_hxxb/CN/abstract/abstract344143.shtml

  13. [13]

      邢垒, 焦丽颖, 物理化学学报, 2016, 32, 2133.Xing, L.; Jiao, L. Y. Acta Phys.-Chim. Sin. 2016, 32, 2133.

  14. [14]

      Raybaud, P.; Hafner, J.; Kresse, G.; Kasztelan, S.; Toulhoat, H. J. Catal. 2000, 189, 129. doi: 10.1006/jcat.1999.2698

  15. [15]

      Toulhoat, H.; Raybaud, P.; Kasztelan, S.; Kresse, G.; Hafner, J. Catal. Today 1999, 50, 629. doi: 10.1016/S0920-5861(98)00497-0

  16. [16]

      Jaramillo, T. F. Nature Chem. 2014, 6, 248. doi: 10.1038/nchem.1853

  17. [17]

      Jaramillo, T. F.; Jørgensen, K. P.; Bonde, J.; Nielsen, J. H.; Horch, S.; Chorkendorff, I. Science 2007, 317, 100. doi: 10.1126/science.1141483

  18. [18]

      Guo, X.; Tong, X.; Wang, Y.; Chen, C.; Jin, G.; Guo, X. Y. J. Mater. Chem. A 2013, 1, 4657. doi: 10.1039/c3ta10600d

  19. [19]

      Liao, L.; Zhu, J.; Bian, X.; Zhu, L.; Scanlon, M. D.; Girault, H. H.; Liu, B. Adv. Funct. Mater. 2013, 23, 5326. doi: 10.1002/adfm.v23.42

  20. [20]

      Kockerling, M.; Johrendt, D.; Finckh, E. W. J. Am. Chem. Soc. 1998, 120, 12297. doi: 10.1021/ja982081t

  21. [21]

      Hernandez-Molina, R.; Gili, P.; Sokolov, M. N.; Safont, V. S. Inorg. Chim. Acta 2011, 376, 10. doi: 10.1016/j.ica.2011.05.023

  22. [22]

      Liao, Y. H.; Park, K. S.; Singh, P.; Li, W.; Goodenough, J. B. J. Power Sources 2014, 245, 27. doi: 10.1016/j.jpowsour.2013.06.048

  23. [23]

      Divigalpitiya, W. M. R.; Frindt, R. F.; Morrison, S. R. J. Phys. D:Appl. Phys. 1990, 23, 966. doi: 10.1088/0022-3727/23/7/035

  24. [24]

      Oviedo-Roa, R.; Martinez-Magadan, J. M.; Illas, F. J. Phys. Chem. B 2006, 110, 7951. doi: 10.1021/jp052299j

  25. [25]

      Lewis, D. A.; Kenney, C. N. Trans. Inst. Chem. Eng. 1981, 59, 186.

  26. [26]

      Aray, Y.; Zambrano, D.; Cornejo, M. H.; Ludeña, E. V.; Iza, P.; Vidal, A. B.; Coll, D. S.; Jimenez, D. M.; Henriquez, F.; Paredes, C. J. Phys. Chem. C 2014, 118, 27823. doi: 10.1021/jp5059269

  27. [27]

      Allali, N.; Marie, A. M.; Danot, M.; Geantet, C.; Breysse, M. J. Catal. 1995, 156, 279. doi: 10.1006/jcat.1995.1255

  28. [28]

      Geantet, C.; Afonso, J.; Breysse, M.; Danot, M. Catal. Today 1996, 28, 23. doi: 10.1016/0920-5861(95)00215-4

  29. [29]

      Allali, N.; Prouzet, E.; Michalowicz, A.; Gaborit, V.; Nadiri, A.; Danot, M. Appl. Catal. A-GEN. 1997, 159, 333. doi: 10.1016/S0926-860X(97)00069-0

  30. [30]

      Cattenot, M.; Portefaix, J. L.; Afonso, J.; Breysse, M.; Lacroix, M.; Perot, G. J. Catal. 1998, 173, 366. doi: 10.1006/jcat.1997.1929

  31. [31]

      Danot, M.; Afonso, J.; Portefaix, J. L.; Breysse, M.; Courieres, T. D. Catal. Today 1991, 10, 629. doi: 10.1016/0920-5861(91)80043-9

  32. [32]

      Afanasiev, P.; Bezverkhyy, I. Appl. Catal. A-GEN. 2007, 322, 129. doi: 10.1016/j.apcata.2007.01.015

  33. [33]

      Gaborit, V.; Allali, N.; Geantet, C.; Breysse, M.; Vrinat, M.; Danotl, M. Catal. Today 2000, 57, 267. doi: 10.1016/S0920-5861(99)00336-3

  34. [34]

      柴永明, 安高军, 柳云骐, 刘晨光, 化学进展, 2007, 19, 234.Chai, Y. M.; An, G. J.; Liu, Y. Q.; Liu, C. G. Prog. Chem. 2007, 19, 234.

  35. [35]

      Besenbacher, F.; Brorson, M.; Clausen, B. S.; Helveg, S.; Hinnemann, B.; Kibsgaard, J.; Lauritsen, J. V.; Moses, P. G.; Nørskovc, J. K.; Topsøe, H. Catal. Today 2008, 130, 86. doi: 10.1016/j.cattod.2007.08.009

  36. [36]

      Drescher, T.; Niefind, F.; Bensch, W.; Grünert, W. J. Am. Chem. Soc. 2012, 134, 18896. doi: 10.1021/ja3074903

  37. [37]

      Prodhomme, P. Y.; Raybaud, P.; Toulhoat, H. J. Catal. 2011, 280, 178. doi: 10.1016/j.jcat.2011.03.017

  38. [38]

      Dinter, N.; Rusanen, M.; Raybaud, P.; Kasztelan, S.; Silva, P.; Toulhoat, H. J. Catal. 2010, 275, 117. doi: 10.1016/j.jcat.2010.07.020

  39. [39]

      Lauritsen, J. V.; Nyberg, M.; Nørskov, J. K.; Clausen, B. S.; Topsøe, H.; Lægsgaard, E.; Besenbacher, F. J. Catal. 2004, 224, 94. doi: 10.1016/j.jcat.2004.02.009

  40. [40]

      Wen, X. D.; Zeng, T.; Li, Y. W.; Wang, J.; Jiao, H. J. Phys. Chem. B 2005, 109, 18491. doi: 10.1021/jp051540r

  41. [41]

      卢嘉锡, 结构化学, 1989, 5, 327.Lu, J. X. Chinese J. Struct. Chem. 1989, 5, 327.

  42. [42]

      黄荣彬, 张鹏, 朱永宝, 郑兰荪, 物理化学学报, 1991, 8, 8. http://www.cnki.com.cn/Article/CJFDTotal-WLHX199201002.htmHuang, R. B.; Zhang, P.; Zhu, Y. B.; Zheng, L. S. Acta Phys-Chim. Sin. 1991, 8, 8. http://www.cnki.com.cn/Article/CJFDTotal-WLHX199201002.htm

  43. [43]

      Popov, I.; Kunze, T.; Gemming, S.; Seifert, G. Eur. Phys. J. D. 2007, 45, 439. doi: 10.1140/epjd/e2007-00170-1

  44. [44]

      Popov, I.; Gemming, S.; Seifert, G. Phys. Rev. B 2007, 75, 245436. doi: 10.1103/PhysRevB.75.245436

  45. [45]

      Seifert, G.; Tamuliene, J.; Gemming, S. Comput. Mater. Sci. 2006, 35, 316. doi: 10.1016/j.commatsci.2004.08.014

  46. [46]

      Gemming, S.; Seifert, G. Appl. Phys. A 2006, 82, 175.

  47. [47]

      Jiao, H. J.; Li, Y. W.; Delmon, B.; Halet, J. F. J. Am. Chem. Soc. 2001, 123, 7334. doi: 10.1021/ja0034085

  48. [48]

      Bertram, N.; Kim, Y. D.; Ganteför, G.; Sun, Q.; Jena, P.; Tamliene, J.; Seifert, G. Chem. Phys. Lett. 2004, 396, 341. doi: 10.1016/j.cplett.2004.08.057

  49. [49]

      Liang, B.; Andrews, L. J. Phys. Chem. A 2002, 106, 3738. doi: 10.1021/jp013790n

  50. [50]

      Liang, B.; Andrews, L. J. Phys. Chem. A 2002, 106, 6945. doi: 10.1021/jp025915+

  51. [51]

      Yu, S. W.; Yin, L. Q.; Yao, L. F.; Li, M.; Xie, X. G. Chin. Chem. Lett. 2008, 19, 1008. doi: 10.1016/j.cclet.2008.05.029

  52. [52]

      Yin, S.; Xie, Y.; Bernstein, E. R. J. Phys. Chem. A 2011, 115, 10266. doi: 10.1021/jp2056267

  53. [53]

      Saha, A.; Raghavachari, K. J. Chem. Phys. 2013, 139, 204301. doi: 10.1063/1.4830096

  54. [54]

      Saha, A.; Raghavachari, K. J. Chem. Phys. 2014, 141, 074305. doi: 10.1063/1.4892671

  55. [55]

      Afanasiev, P.; Fischer, L.; Beauchesne, F.; Danot, M.; Gaborit, V.; Breysse, M. Catal. Lett. 2000, 64, 59. doi: 10.1023/A:1019058113931

  56. [56]

      Gaborit, V.; Allali, N.; Danot, M.; Geantet, C.; Cattenot, M.; Breysse, M.; Diehl, F. Catal. Today 2003, 78, 499. doi: 10.1016/S0920-5861(02)00336-X

  57. [57]

      Aray, Y.; Zambrano, D.; Cornejo, M. H.; Ludeña, E. V.; Iza, P.; Vidal, A. B.; Coll, D. S.; Jimenez, D. M.; Henriquez, F.; Paredes, C. J. Phys. Chem. C 2014, 118, 27823. doi: 10.1021/jp5059269

  58. [58]

      Ivanovskaya, V. V.; Heine, T.; Gemming, S.; Seifert, G. Phys. Status. Solidi. 2006, 243, 1757. doi: 10.1002/(ISSN)1521-3951

  59. [59]

      Ivanovskaya, V. V.; Zobelli, A.; Gloter, A.; Brun, N.; Serin, V.; Colliex, C. Phys. Rev. B:Condens. Matter 2008, 78, 134104. doi: 10.1103/PhysRevB.78.134104

  60. [60]

      Deepak, F. L.; Cohen, H.; Cohen, S.; Feldman, Y.; Popovitz-Biro, R.; Azulay, D.; Millo, O.; Tenne, R. J. Am. Chem. Soc. 2007, 129, 12549. doi: 10.1021/ja074081b

  61. [61]

      Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Montgomery, J. A., Jr.; Vreven, T.; Kudin, K. N.; Burant, J. C.; Millam, J. M.; Iyengar, S. S.; Tomasi, J.; Barone, V.; Mennucci, B.; Cossi, M.; Scalmani, G.; Rega, N.; Petersson, G. A.; Nakatsuji, H.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Klene, M.; Li, X.; Knox, J. E.; Hratchian, H. P.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R.; Pomelli, C.; Ochterski, J. W.; Ayala, P. Y.; Morokuma, K.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Zakrzewski, V. G.; Dapprich, S.; Daniels, A. D.; Strain, M. C.; Farkas, O.; Malick, D. K.; Rabuck, A. D.; Raghavachari, K.; Foresman, J. B.; Ortiz, J. V.; Cui, Q.; Baboul, A. G.; Clifford, S.; Cioslowski, J.; Stefanov, B. B.; Liu, G.; Liashenko, A.; Piskorz, P.; Komaromi, I.; Martin, R. L.; Fox, D. J.; Keith, T.; Al-Laham, M. A.; Peng, C. Y.; Nanayakkara, A.; Challacombe, M.; Gill, P. M. W.; Johnson, B.; Chen, W.; Wong, M. W.; Gonzalez, C.; Pople, J. A., Gaussian 03, Revision D. 01, Gaussian, Inc.:Wallingford, CT, 2004.

  62. [62]

      Becke, A. D. J. Chem. Phys. 1993, 98, 1372. doi: 10.1063/1.464304

  63. [63]

      Lee, C.; Yang, W. T.; Parr, R. G. Phys. Rev. B 1988, 37, 785. doi: 10.1103/PhysRevB.37.785

  64. [64]

      Stephens, P. J.; Devlin, F. J.; Chabalowski, C. F.; Frisch, M. J. Phys. Chem. 1994, 98, 11623. doi: 10.1021/j100096a001

  65. [65]

      Schafer, A.; Huber, C.; Ahlrichs, R. J. Chem. Phys. 1994, 100, 5829. doi: 10.1063/1.467146

  66. [66]

      Weigend, F.; Ahlrichs, R. Phys. Chem. Chem. Phys. 2005, 7, 3297. doi: 10.1039/b508541a

  67. [67]

      Eichkorn, K.; Weigend, F.; Treutler, O.; Ahlrichs, R. Theor. Chem. Acc. 1997, 97, 119. The exponents (included those of the polarization functions) and contraction coefficients can be retrieved from the following web-site:https://bse.pnl.gov/bse/portal.

  68. [68]

      Andrae, D.; Häußermann, U.; Dolg, M.; Stoll, H.; Preuß, H. Theor. Chim. Acta 1990, 77, 123. doi: 10.1007/BF01114537

  69. [69]

      Kuchle, W.; Dolg, M.; Stoll, H.; Preuss, H. Pseudopotentials of the Stuttgart/Dresden Group 1998, revision August 11, 1998; < http://www.theochem.uni-stuttgart.de/pseudopotentiale > .

  70. [70]

      Dunning, T. H. Jr. J. Chem. Phys. 1989, 90, 1007. doi: 10.1063/1.456153

  71. [71]

      Martin, J. M. L.; Sundermann, A. J. Chem. Phys. 2001, 114, 3408. doi: 10.1063/1.1337864

  72. [72]

      Woon, D. E.; Dunning, T. H. Jr. J. Chem. Phys. 1993, 98, 1358. doi: 10.1063/1.464303

  73. [73]

      Dunning, T. H. Jr.; Peterson, K. A.; Wilson, A. K. J. Chem. Phys. 2001, 114, 9244. doi: 10.1063/1.1367373

  74. [74]

      Purvis, G. D.; Bartlett, R. J. J. Chem. Phys. 1982, 76, 1910. doi: 10.1063/1.443164

  75. [75]

      Scuseria, G. E.; Janssen, C. L.; Schaefer Ⅲ, H. F. J. Chem. Phys. 1988, 89, 7382. doi: 10.1063/1.455269

  76. [76]

      Raghavachari, K.; Trucks, G. W.; Pople, J. A.; Head-Gordon, M. Chem. Phys. Lett. 1989, 157, 479. doi: 10.1016/S0009-2614(89)87395-6

  77. [77]

      Watts, J. D.; Gauss, J.; Bartlett, R. J. J. Chem. Phys. 1993, 98, 8718. doi: 10.1063/1.464480

  78. [78]

      Bartlett, R. J.; Musial, M. Rev. Mod. Phys. 2007, 79, 291. doi: 10.1103/RevModPhys.79.291

  79. [79]

      Werner, H. J.; Knowles, P. J.; Knizia, G.; Manby, F. R.; Schütz, M.; Celani, P.; Györffy, W.; Kats, D.; Korona, T.; Lindh, R.; Mitrushenkov, A.; Rauhut, G.; Shamasundar, K. R.; Adler, T. B.; Amos, R. D.; Bernhardsson, A.; Berning, A.; Cooper, D. L.; Deegan, M. J. O.; Dobbyn, A. J.; Eckert, F.; Goll, E.; Hampel, C.; Hesselmann, A.; Hetzer, G.; Hrenar, T.; Jansen, G.; Köppl, C.; Liu, Y.; Lloyd, A. W.; Mata, R. A.; May, A. J.; McNicholas, S. J.; Meyer, W.; Mura, M. E.; Nicklaß, A.; O'Neill, D. P.; Palmieri, P.; Peng, D.; Pflüger, K.; Pitzer, R.; Reiher, M.; Shiozaki, T.; Stoll, H.; Stone, A. J.; Tarroni, R.; Thorsteinsson, T.; Wang, M., MOLPRO, Version 2010. 1, a package of ab initio programs, < http://www.molpro.net > .

  80. [80]

      Dennington, R. Ⅱ; Keith, T.; Millam, J. GaussView, Version 4. 1. 2., Semichem Inc., Shawnee Mission, 2007.

  81. [81]

      Tozer, D. J.; Handy, N. C. J. Chem. Phys. 1998, 109, 10180. doi: 10.1063/1.477711

  82. [82]

      Zhang, S.; Luo, C. G.; Li, H. Y.; Lu, C.; Li, G. Q.; Lu, Z. W. Mater. Chem. Phys. 2015, 160, 227. doi: 10.1016/j.matchemphys.2015.04.028

  83. [83]

      Zhang, S.; Zhang, Y.; Lu, Z.; Shen, X.; Li, G.; Peng, F.; Bu, X. J. Mater. Sci. 2016, 51, 9440. doi: 10.1007/s10853-016-0189-9

  84. [84]

      Merki, D.; Fierro, S.; Vrubel, H.; Hu, X. Chem. Sci. 2011, 2, 1262. doi: 10.1039/C1SC00117E

  85. [85]

      Duchet, J. C.; Van-Oers, E. M.; De-Beer, V. H. J.; Prins, R. J. Catal. 1983, 80, 386. doi: 10.1016/0021-9517(83)90263-4

  86. [86]

      Afanasiev, P.; Jobic, H.; Lorentz, C.; Leverd, P.; Mastubayashi, N.; Piccolo, L.; Vrinat, M. J. Phys. Chem. C 2009, 113, 4139. doi: 10.1021/jp809300y

  87. [87]

      Afanasiev, P. J. Catal. 2010, 269, 269. doi: 10.1016/j.jcat.2009.11.004

  88. [88]

      Allali, N.; Leblanc, A.; Danot, M.; Geantet, C.; Vrinat, M.; Breysse, M. Catal. Today 1996, 27, 137. doi: 10.1016/0920-5861(95)00181-6

  89. [89]

      Christe, K. O.; Dixon, D. A.; Mclemore, D.; Wilson, W. W.; Sheehy, J. A.; Boatz, J. A. J. Fluorine Chem. 1999, 101, 151.

  90. [90]

      Li, S.; Dixon, D. A. J. Phys. Chem. A 2006, 110, 6231. doi: 10.1021/jp060735b

• 

  图 1  在B3LYP/Basis-Ⅱ水平下得到的NbMoS₃^-/0体系最稳构型及与其相对能量靠近的异构体 (键长单位为 )

  Figure 1  Optimized structures for NbMoS₃^-/0 at the B3LYP/Basis-Ⅱ level of theory. The relative energies are in eV and the bond lengths are in angstroms

  下载: 全尺寸图片 幻灯片
  

  图 2  在B3LYP/Basis-Ⅱ水平下得到的NbMoS₄^-/0体系最稳构型及与其相对能量靠近的异构体 (键长单位为 )

  Figure 2  Optimized structures for NbMoS₄^-/0 at the B3LYP/Basis-Ⅱ level of theory. The relative energies are in eV and the bond lengths are in angstroms

  下载: 全尺寸图片 幻灯片
  

  图 3  在B3LYP/Basis-Ⅱ水平下得到的NbMoS₅^-/0体系最稳构型及与其相对能量靠近的异构体 (键长单位为 )

  Figure 3  Optimized structures for NbMoS₅^-/0 at the B3LYP/Basis-Ⅱ level of theory. The relative energies are in eV and the bond lengths are in angstroms

  下载: 全尺寸图片 幻灯片
  

  图 4  在B3LYP/Basis-Ⅱ水平下得到的NbMoS₆^-/0体系最稳构型及与其相对能量靠近的异构体 (键长单位为 )

  Figure 4  Optimized structures for NbMoS₆^-/0 at the B3LYP/Basis-Ⅱ level of theory. The relative energies are in eV and the bond lengths are in angstroms

  下载: 全尺寸图片 幻灯片
  

  图 5  在B3LYP/Basis-Ⅱ水平下得到的NbMoS₇^-/0体系基态和与其相对能量靠近的异构体 (键长单位为 )

  Figure 5  Optimized structures for NbMoS₇^-/0 at the B3LYP/Basis-Ⅱ level of theory. The relative energies are in eV and the bond lengths are in angstroms

  下载: 全尺寸图片 幻灯片
  

  图 6  模拟NbMoS_n^-(n＝3~7) 阴离子基态及其竞争结构的光电子能谱图 (黑线:一重态; 红线:三重态)

  Figure 6  Simulated photoelectron spectra from the ground states and selected low-lying isomers of NbMoS_n^-(n＝3~7) clusters at the B3LYP//Basis-Ⅱ level of theory. (Singlets show in black lines and triplets in red lines) The simulations are done by fitting the distribution of calculated VDEs with unit-area Gaussian functions of 0.1 eV width

  下载: 全尺寸图片 幻灯片
  

  图 7  NbMoS_n (n＝3~7) 基态构型的电子自旋密度 (|e|) 示意图 (蓝色区域代表单电子的分布, 黑色数值代表自旋密度值)

  Figure 7  Electron spin density (in |e|) for the ground states of NbMoS_n (n＝3~7) clusters

  下载: 全尺寸图片 幻灯片
  

  图 8  NbMoS₃^-/0基态的价层分子轨道图

  Figure 8  Valence molecular orbitals for the ground states of (a) NbMoS₃ and (b) NbMoS₃^-

  下载: 全尺寸图片 幻灯片
  

  图 9  NbMoS₄^-/0基态及其竞争结构的价层分子轨道图

  Figure 9  Valence molecular orbitals for the ground states and selected low-lying isomer of NbMoS₄ and NbMoS₄^-

  下载: 全尺寸图片 幻灯片
  

  图 10  NbMoS₅^-/0基态及其竞争结构的价层分子轨道图

  Figure 10  Valence molecular orbitals for the ground states and selected low-lying isomer of NbMoS₅ and NbMoS₅^-

  下载: 全尺寸图片 幻灯片
  

  图 11  基态NbMoS₅^-/0的价层分子轨道图

  Figure 11  Valence molecular orbitals for the ground states of (a) NbMoS₆ and (b) NbMoS₆^-

  下载: 全尺寸图片 幻灯片
  

  图 12  基态NbMoS₇^-/0的价层分子轨道图

  Figure 12  Valence molecular orbitals for the ground states of (a) NbMoS₇ and (b) NbMoS₇^-

  下载: 全尺寸图片 幻灯片
  

  图 13  基态阴离子NbMoS_n^-(n＝3~7) VDE_1st与ADE随硫含量的变化趋势图

  Figure 13  The calculated VDE_1st and ADE of NbMoS_n^-(n＝3~7) as a function of S content (n)

  下载: 全尺寸图片 幻灯片
  

  图 14  在B3LYP/Basis-Ⅱ水平下得到的基态NbMoS_n^-/0(n＝3~7) 构型

  Figure 14  Optimized ground states for NbMoS_n^-/0(n＝3~7) clusters at the B3LYP/Basis-Ⅱ level of theory

  下载: 全尺寸图片 幻灯片
  

  图 15  NbMoS_n^-/0(n＝3~7) 团簇的平均结合能E_b与能量二阶差分△₂E随硫含量的变化趋势图

  Figure 15  The averaged binding energy (E_b) and second-order energy difference (△₂E) of NbMoS_n^-/0(n＝3~7) as a function of S content (n)

  下载: 全尺寸图片 幻灯片

  表 1  NbMoS_n^-(n＝3~7) 在不同计算水平下的相对能量及其绝热电子逸出能 (ADE) 与第一点垂直电子逸出能 (VDE_1st) 的结果

  Table 1.  Relative energies of selected low-lying isomers of NbMoS_n^-(n＝3~7) with different basis sets, and comparisons with those from the CCSD (T) single-point calculations at the B3LYP geometries together with the corresponding ADE and the first VDE values

  Cluster	B3LYP/Basis-Ⅰa, b	B3LYP/Basis-Ⅱa, c	CCSD (T)-SPa, d	ADE a	VDE1sta
  NbMoS3-(C3v 1A1)	0.00	0.00	0.00	2.54	2.87
  NbMoS3-(Cs 3A″)	0.10	0.18	0.48	2.36	2.65
  NbMoS3-(Cs 1A')	0.15	0.20	0.35	2.35	3.01
  NbMoS4-(Cs 3A″)	0.00	0.00	0.13	2.93	3.33
  NbMoS4-(Cs 5A″)	0.02	0.03	0.24	2.90	3.75
  NbMoS4-(Cs 5A″)	0.04	0.05	0.25	2.88	3.80
  NbMoS4-(C3v 3A1)	0.25	0.24	0.26	2.69	3.07
  NbMoS4-(Cs 3A')	0.26	0.27	0.43	2.66	2.97
  NbMoS4-(Cs 1A')	0.30	0.30	0.00	2.63	2.81
  NbMoS5-(Cs 3A')	0.00	0.00	0.19	3.49	3.82
  NbMoS5-(Cs 1A')	0.05	0.06	0.00	3.43	3.68
  NbMoS5-(Cs 3A″)	0.21	0.18	0.26	3.31	3.73
  NbMoS5-(Cs 1A')	0.22	0.23	0.34	3.25	3.95
  NbMoS5-(Cs 3A')	0.23	0.24	0.46	3.24	3.84
  NbMoS6-(Cs 1A')	0.00	0.00	0.00	4.27	4.69
  NbMoS7-(C1 1A)	0.00	0.00	0.00	4.13	4.46
  NbMoS7-(C1 1A)	0.13	0.15	0.11	3.98	4.48
  aAll energies are in eV; b B3LYP/Basis-Ⅰ; cB3LYP/Basis-Ⅱ; dCCSD (T) single-point calculations at the B3LYP/Basis-Ⅱ geometries.

  下载: 导出CSV

  表 2  在B3LYP/Basis-Ⅱ水平下得到的反应 (4) 吉布斯自由能变化值∆G

  Table 2.  Calculated free energy differences (ΔG) for the proposed reaction (4) at the B3LYP/Basis-Ⅱ level of theory

  n→n－1	∆Gnua, b	∆Gana, b
  4→3	34.92	37.07
  5→4	25.09	43.44
  6→5	9.90	30.96
  7→6	0.77	－3.43
  a∆Gnu and ∆Gan mean ∆G of the neutral and anionic clusters, respectively. bAll energies are in kcal•mol－1.

  下载: 导出CSV

  表 3  方程 (7) 的氟亲和能FA

  Table 3.  Equation (7) for the values of fluorine affinity (FA)

  Cluster	FAa
  NbMoS3	4.68
  NbMoS4	5.18
  NbMoS5	5.69
  NbMoS6	4.37
  NbMoS7	3.77
  a All energies are in eV.

  下载: 导出CSV
•