English

• 

  1   引言

  自Staudinger提出高分子的概念以来, 高分子科学和高分子材料工业的发展可谓突飞猛进.高分子材料成为材料领域的研究热点, 已在国民经济, 国防科技和尖端技术等各个领域得到了广泛应用^[1].高分子溶液是人们在生产和实践过程中最常遇见的对象, 溶液中高分子的单链或者凝聚态结构对最终高分子材料成品的结构与性能往往会有非常大的影响.因此, 对高分子在溶液中的基础研究是高分子科学的重要内容.

  高分子单链分子一般都有较多的结构单元, 而且分子量巨大, 结构复杂; 更重要的是, 高分子链还具有自相似性和分形性的特点.因此, 它具有其他凝聚态物质所不具有的标度性.法国科学家De Gennes在其论著《高分子物理学中的标度概念》中对相关内容给予了深入阐述^[2].表征高分子特性的函数可以写成一个系数因子乘以一个标度形式, 即用一个简单指数方程(y＝kx^b), 将两种不同物理变量建立非线性联系.其中:前置系数k通常由单体的性质决定, 而由长链决定的物理性质则出现在标度律中.幂指数b就是标度参数, 通常不等于1(等于1, 即线性关系)^[1].这一概念的提出得到了科学界的高度关注, 目前, 已成为高分子科学领域重要且基础的概念和理论工具.由于高分子的分子量具有多分散性, 故高分子具有复杂的非线性特征, 这使得人们对高分子的研究步履艰难.标度律以指数律的形式, 为人们探究结构和行为均比较复杂的高分子世界的规律提供了形式简单的理论工具^[3].更进一步, 由于自相似、分形等概念的引入, 人们发现在高分子溶液聚集方面也存在较多指数律关系.因此, 指数律虽是一种简单的数学方程, 但它可直观、深刻的描述高分子的非线性行为, 揭示软物质从无序到有序变化的一般规律.采用指数律, 可清晰地描述真实分子链的构象及在不同溶液中的形态; 也可描述在亚浓溶液乃至浓厚体系中分子链聚集状态在外场刺激下的变化过程及规律.这对了解高分子链在溶液中的本征性质及其在固态薄膜与高效率功能器件的应用意义重大^[3].

  目前, 越来越多独具特色的高分子材料被发现或合成, 但人们对其在溶液中的链构象和聚集态结构等本征性质了解甚微.事实上, 高分子各种物理性质都与其溶液性质相关.因此, 利用指数规律研究高分子在溶液中的单链及凝聚态形态结构, 揭示其结构的转变、结构单元的运动规律, 将会加深对高分子物理本质的认识, 构筑性能更加优良的高分子材料.

  本文总结了一些通常用于高分子指数律研究的手段:如光散射法、小角中子散射法和黏度法以及指数律在天然生物、枝化、共轭等高分子溶液中的应用.包括这些聚合物在溶液中单链和聚集体的研究.

  2   几种常见的利用指数律研究高分子溶液的方法

  2.1   黏度法

  一般来说, 当高分子溶液较稀、低于临界接触浓度时, 溶液中分子链由于相互远离而成为孤立的单链, 此时溶液黏度性质仅仅与分子量大小有关.实验证明, 当聚合物、溶剂及温度确定时, 溶液的特性黏度[η]值仅与聚合物黏均分子量M_η有关, [η]与M_η的关系符合Mark-Houwink方程式:

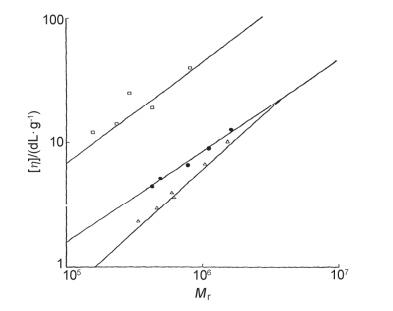
  其中α为Mark-Houwink指数, 其数值与分子链的形状有关^{[4, 5]}, 可通过测定聚合物溶液的黏度[η]和黏均分子量M_η得到, 如图 1所示.一些常见的聚合物-溶液体系的α值可在有关手册中查询, 表 1给出了部分体系的α值.总体而言, 当高分子链是无规柔性线团时, α值在0.5～0.6之间; 而当高分子链是棒状结构时, α值大概是1.0^[4].

  图 1  通过高分子稀溶液中黏均分子量M_η和特性黏度[η]之间的双对数图, 得到Mark-Houwink指数α Figure 1.  The Mark-Houwink index α was obtained from the double logarithmic plot of intrinsic viscosity [η] against viscosity-average molecular weight M_η^[4]

  图选项

  下载全尺寸图像

  下载幻灯片

  表 1  Mark-Houwink指数α值对应的分子链形状 Table 1.  The molecular chain shape corresponding to the value of Mark-Houwink index α

  表选项

  导出Excel

  下载全尺寸表图像

  Mark-Houwink index α	0.33	0.5～0.6	1.0
  分子链形状	球状	柔性无规线团	棒状

  表 1  Mark-Houwink指数α值对应的分子链形状
  Table 1.  The molecular chain shape corresponding to the value of Mark-Houwink index α

  Teraoka等^[5]的研究认为, 在θ溶剂中, 柔性链的α＝0.5;在良溶剂中, 柔性链的α在0.7～0.8之间; 而刚性链的α值则大于1.可见, 当指数α越大, 链越伸展.这是由于同样伸直长度的分子链, 指数大的在溶液中的运动摩擦力将会更大.因此, 根据这一规律, 用黏度法测定不同分子量聚合物在稀溶液中的特性黏度, 再根据Mark-Houwink方程得出幂指数α, 可判断分子链在溶液中的形状.

  2.2   激光光散射法

  静态光散射法是最常用于高分子溶液表征的方法.静态光散射法可以测定高分子稀溶液中单链的均方根回旋半径 < s² > z^1/2, 即R_g.它是用于高分子溶液研究的重要参数, 反映了高分子的平均尺寸大小.对于高分子单链而言, 显然分子量不同时, 其在稀溶液中的R_g也不同; 但由于高分子在溶液中的形状并非直链棒状而形态多样.因此, R_g与高分子分子量之间的关系也并非线性, 而是存在如下非线性指数关系:

  其中:幂指数v是分子形状的一个特征参数, 其值反映了分子链的不同形状, 可通过测定聚合物单链的R_g和重均分子量得到.如图 2所示, 当指数v分别为0.33, 0.50～0.60和1时, 分子链的形状是球状、无规线团和刚性直链^[6～8].而它的倒数d_f＝1/v, 也有特殊的物理意义: d_f被称为分形维数.如果d_f＝1, 分子链即为棒状直链; R_g随着M_w线性增加, d_f＝5/3～2时, 高分子链呈现高斯线团状; 枝化作用会使得d_f稍微增加, d_f＝2时, 分子链呈现二维片状; 而若d_f＝3, 则分子链呈现密度分布均匀的三维球体^[9～11].因此, 通过静态光散射测定分子链的均方根回旋半径R_g, 建立R_g与聚合物的重均分子量M_w之间的指数关系得到分形维数d_f, 便可依此判断分子链在溶液中的形状.

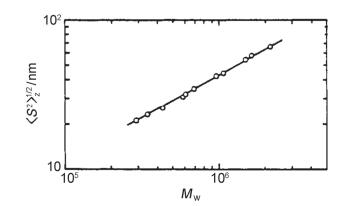  图 2  重均分子量M_w和均方根回转半径R_g( < s² > ^1/2)之间的指数关系 Figure 2.  Exponential relationship between the root mean square radius of gyration R_g ( < s² > ^1/2) and weight-average molecular weight M_w^[6]

  图选项

  下载全尺寸图像

  下载幻灯片

  此外, 这一公式还可以用于表征溶液中聚集体的形态结构^{[12, 13]}.聚集体的表观分子量和R_g也存在同样的指数关系, 形状指数v的大小代表了聚集的形状.当v＝1/3时, 聚集体是均匀球状; 当v＝1/2时, 呈无规线团状; 而当v＝1时, 聚集体呈直棒状; 其形状与单链一致.

  据报道^[14～17], 在静态光散射测试过程中, 各角度测试得到的散射光强度I与散射矢量q之间也存在着指数关系:

  其中: q＝(4πn/λ)sin(θ/2), d_f就是溶液中粒子的分形维数.可根据d_f的值判断溶液中粒子的形态结构.如图 3所示, 其中R_agg < q^－1 < R₀(R_agg、R₀分别为聚集和单链的均方根回旋半径); d_f则是聚集的分形维数, 可根据d_f的值判断单链和聚集体的形态结构.

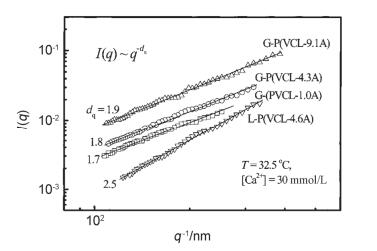  图 3  静态光散射(SLS)表征光强函数I(q)和散射矢量q之间的指数关系 Figure 3.  Exponential relationship between the excess scattering intensity I(q) and the scattering vector q by static light scattering (SLS)^[17]

  图选项

  下载全尺寸图像

  下载幻灯片

  由于激光是可见光, 波长一般在几百纳米, 这将导致散射矢量的倒数1/q比较大(一般远大于高分子单链的R_g).因此, 光散射法多用于表征高分子溶液中的聚集态结构.

  2.3   小角中子/X射线散射法

  小角中子/X射线散射法皆是用于高分子溶液研究的重要手段, 可测定溶液中单链结构和聚集行为^[18～24], 其测量原理类似于激光光散射法.如图 4所示, 各角度测得的光强与散射矢量同样满足如下指数关系式:

  图 4  小角中子散射法中光强函数I(q)和散射矢量q之间的指数关系 Figure 4.  Exponential relationship between the excess scattering intensity I(q) and the scattering vector q by small angle neutron scattering (SANS)^[22]

  图选项

  下载全尺寸图像

  下载幻灯片

  与激光光散射法不同的关键点在于:中子和X射线的波长( < 1 nm)远远小于激光波长( > 100 nm), 散射矢量倒数1/q要远远小于激光光散射的1/q值, 故更容易测量到单链结构.这两种方法常用于测定各角度的散射光强I与散射矢量q之间的指数关系, 而得到单链和聚集的分形维数, 从而能更深入地研究高分子溶液中单链、聚集体的形态结构及从单链到聚集的动力学演变过程^[20～24].

  2.4   核磁共振法(NMR)

  结合Sketjal-Tanner方程, 核磁共振法可用于表征高分子稀溶液中溶质的平移扩散运动, 从而得到溶液中粒子的扩散系数D.在许多研究中人们发现:如果分子是均匀分布的, 则其扩散系数D与分子量M之间将存在指数关系:

  这一公式常被用于预测分子量^{[25, 26]}, 如图 5所示.由于此公式在形式上类似于公式(2), 也有很多人认为δ等同于v. Delsuc等^[27]专门从实验和理论上对比了这两个参数的相关性, 最终发现当测量粒子的密度分布均匀时, 这一指数δ与v是等同的.这一指数关系已用于表征溶液粒子的分形维数, 从而得到高分子单链或聚集体在溶液中的形态结构^[28].

  图 5  核磁共振法中扩散系数D与重均分子量M_w之间的指数关系 Figure 5.  Exponential relationships between the diffusion coefficient (D) and the weight-average molecular weight M_w via the nuclear magnetic resonance (NMR)^[25]

  图选项

  下载全尺寸图像

  下载幻灯片

  3   利用指数律研究高分子溶液中的单链构象

  高分子溶液中的单链构象反映了高分子单链在溶液中的形态结构, 是高分子最重要的基本物理特征.高分子的链结构就像建筑物的基本材料——砖瓦, 各具特色的砖瓦决定了建筑物的基本性能; 同样地, 高分子的链结构特征决定了高分子材料的基本性能^[3].因此, 研究高分子单链的结构特征对于高分子材料的分子设计及优异性能的高分子产品的开发具有重要指导意义^[29].这里, 我们将从高分子的不同种类切入, 介绍如何用指数规律研究不同类型的高分子单链.

  3.1   天然生物类高分子

  目前, 许多人工合成的高分子材料因其高毒性, 难降解给人们的生活带来了很大的危害.天然类高分子由于其取材方便、对环境友好、低毒、低危害、而且生物活性好等优点得到了科学家们的高度重视, 相当多的天然生物类高分子如多糖、蛋白质、DNA等被研究并应用于生物材料等领域.而溶液中的链构象对此类高分子生物活性和进一步加工应用影响重大.因此, 关于此类高分子在溶液中的链构象研究比较多, 利用指数规律研究其高分子单链构象的报道亦多见^[30～37].

  早在1982年, Tokuya等^[6]就对支链淀粉在水溶液中的链构象进行了研究.他们利用沉淀分级的方法对原始样品进行分级, 得到一系列窄分布的不同分子量样品, 然后利用黏度和光散射法分别得到了支链淀粉在水中的M-H(Mark-Houwink)指数α 0.5;和分形维数倒数(d_f＝1/v)0.57, 依此确定其在溶液中的链构象是伸展的柔性线团. Norisuye等^[31]在1984年根据公式(2)研究了黄原胶在0.1 mol/L的NaCl水溶液和氢氧化镉乙二胺溶液中的链构象, 发现在M_w低于3×10⁵时, 水溶液中的链构象呈刚性; 而当高于此分子量时, 链构象呈半刚性. Cui等^[32]利用黏度法和动静联用光散射的方法测定了小麦β-葡聚糖单链在NaOH水溶液中的M-H指数α、分形维数倒数(d_f)(如图 6所示), 和形状参数(R_g/R_h), 这三个参数相互验证.最终得出结论:小麦β-葡聚糖在NaOH溶液中呈现无规卷曲的链构象, 而且符合圆柱蠕虫模型.

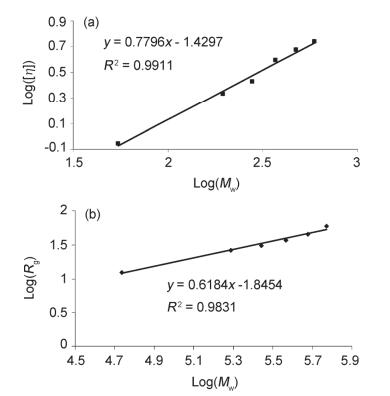  图 6  (a)小麦β-葡聚糖在0.5 mol/L的NaOH溶液中特性黏度[η]的对数与重均分子量M_w之间的指数关系图. (b)小麦β-葡聚糖在0.5 mol/L的NaOH溶液中均方根回旋半径R_g的对数与重均分子量M_w之间的指数关系图 Figure 6.  (a) Double logarithmic plot of [η] against M_w of wheat β-glucan in 0.5 mol/L NaOH solution. (b) Double logarithmic plot of the molecular weight M_w vs the radius of gyration R_g of wheat β-glucan in 0.5 mol/L NaOH solution^[32]

  图选项

  下载全尺寸图像

  下载幻灯片

  张俐娜等^[33～35]利用指数规律研究了许多类型的多糖类物质, 如β-葡聚糖, 虎奶菇中提取的不溶于水的多聚糖和竹节参多糖(如图 7所示).在这些研究中, 他们都利用了黏度法和光散射法, 依据公式(1)和(2)研究了这些多糖类物质的单链构象, 并得到这些物质在各自良溶剂中的M-H指数α和分形维数D, 结合TEM(透射电镜)和AFM(原子力显微镜), 最终判断它们在溶液中的单链形状分别为刚性三螺旋构象、球状构象和球状链构象.研究中他们将SEC(尺寸排除色谱)和SLS(静态光散射)联用, 从而更加快捷地得到了不同分子量多糖的形状信息^{[34, 35]}.

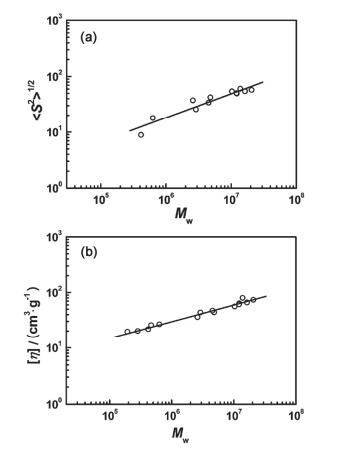  图 7  (a)水溶性多聚糖(TM3a)在0.25 mol/L的LiCl/DMSO溶液中均方根回旋半径 < s² > ^1/2(R_g)的对数与重均分子量M_w之间的指数关系图. (b)水溶性多聚糖(TM3a)在0.25 mol/L的LiCl/DMSO中特性黏度[η]的对数与重均分子量M_w之间的指数关系图 Figure 7.  (a) Plot of log < s² > ^1/2(R_g) vs log M_w for TM3a in 0.25 mol/L LiCl/DMSO. (b) Double logarithmic plot of [η] against M_w of TM3a in 0.25 mol/L LiCl/DMSO^[33]

  图选项

  下载全尺寸图像

  下载幻灯片

  3.2   超枝化高分子

  超枝化高分子是一类比较重要的高分子材料, 最早产生于合成反应的副反应.但近30年来, 超枝化高分子越加受到人们的重视而成为合成高分子的重要部分.原因在于超枝化高分子可引入各类官能团并形成各式各样的结构, 从而得到性质各异的高分子材料.目前, 枝化的控制已经成为设计、合成大分子功能材料的重要手段^[36].然而, 如何表征合成产物的结构也成为了科学家们关注的焦点.超枝化高分子的结构虽然比较复杂, 但其特性黏度、均方回旋半径等参数仍然与分子量有关.因此, 利用指数规律可以表征超支化高分子单链的形状, 密度及自相似性.

  对超支化高分子在溶液中的M-H(Mark-Houwink)指数α的研究已有很多报道.结果显示: α皆处于0.3～0.5之间^[37], 表明超支化大分子的形态结构介于二维盘状和三维球状之间.值得注意的是:在这些研究中, 均利用了SEC和黏度测定联用的装置^{[37, 38]}(如图 8所示).使得黏度和分子量之间的指数关系符合线性规律.但是对于树枝状大分子, 指数关系会逐渐偏离理想曲线.原因在于树枝状大分子分子量的增加将导致分子密度增加以至于分子的均匀性下降^{[39, 40]}, 使得M-H指数随着分子量增加而逐渐减小, 最终趋近于0, 即分子链会变得越来越紧密.有报道称:当分子量达到100000时, 黏度将会达到最大值.

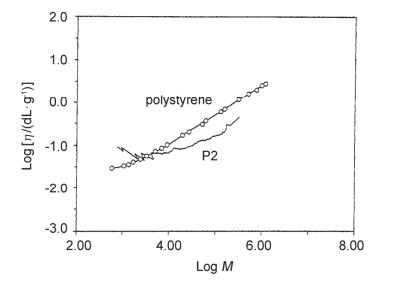  图 8  由SEC和黏度测定联用装置测定的两种超支化聚酯的特性黏度[η]的对数与重均分子量M_w之间的指数关系图 Figure 8.  Plot of log [η] vs log [M_w] for two kinds of hyperbranched polyester as obtained from size-exclusion chromatography (SEC) & viscosity determination device^[38]

  图选项

  下载全尺寸图像

  下载幻灯片

  理论预测无规枝化高分子在良溶剂和θ溶剂中的d_f分别是2.0和2.28^[41～43], 而研究发现超支化高分子的d_f值一般在2～3之间, 例如超支化聚酯的d_f是2.5^[44], 与葡聚糖和淀粉的d_f值接近^{[45, 46]}.而理想的树枝状高分子的d_f接近于3, 即接近于三维球体.

  3.3   共轭类聚合物

  共轭类聚合物是一类具有光电功能的材料, 在过去的30年发展迅猛.被广泛应用于聚合物发光二极管、有机太阳能电池、激光发射器等领域.目前报道大多集中于材料合成、器件性能的提高方面, 但鲜见溶液中单链形态的报道.然而, 共轭聚合物在前体溶液中的形态与其薄膜的聚集态结构及光电器件性能有本质上的联系, 已成为业内人士的共识.因此, 研究共轭聚合物的单链构象对调控其薄膜的凝聚态结构, 提高载流子迁移率及其光电器件效率意义重大.

  我们组^[47]研究了共轭聚合物聚(9, 9-二辛基芴) (PFO)在氯仿中的单链α构象.利用沉淀分级方法, 得到窄分布的不同分子量PFO样品, 然后根据M-H黏度方程(1)得到了M-H指数α 1.44;结合形状参数R_g/R_h, 判断PFO在氯仿溶液中的链构象是半刚性疏松链. Knaapila等^[48]则利用小角中子散射研究了侧链长度对聚芴溶解性的影响.根据公式(3)得到不同侧链长度聚芴的光强-散射矢量之间的指数关系, 发现在不同的侧链长度下, PF衍生物的溶解性各不相同(如图 9): PF9和PF8在甲苯溶液中的分形维数为1, 即表示可溶解成单链; 但PF7和PF6的分形维数是2, 则表示它们的溶解性相对较差, 会形成片状聚集.

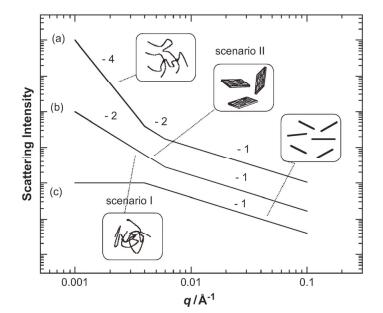  图 9  由散射数据得到的光强I(q)与散射矢量q之间的指数关系, 得到PF衍生物在甲苯溶液中的结构: (a)有交联点的网状结构; (b)高斯线团转变的棒状粒子(设想I)或者有节点的网状结构(设想II); (c)完全溶解的棒状结构(实质是单链) Figure 9.  Schematic description of the scattering data and proposed structures of PFs in toluene: (a) a network-like structure with cross-linked nodes; (b) a structure of rodlike particles forming Gaussian coils (scenario I) or sheet-like aggregates (scenario II) in the longer length scales, and (c) a structure of fully dissolved rod like particles (essentially single polymer chains)^[48]

  图选项

  下载全尺寸图像

  下载幻灯片

  4   用指数规律研究高分子溶液中的凝聚态结构

  高分子凝聚态结构是高分子溶液研究中的重要部分, 当高分子溶液的条件, 如温度、溶剂或者溶质浓度发生改变时, 大量的单链会聚集, 从而形成不同形状和尺寸的聚集体.研究这些聚集体的凝聚态结构、尺寸、特征及形成动力学, 对其在光电、生物、医药、材料等领域应用意义重大.然而, 一条条孤立的单分子链是如何凝聚到一起的？其单链与聚集态结构是否相同？有何不同？其凝聚态的动力学演变过程的机制如何？变化规律如何？迄今鲜见报道.指数规律恰是一种用于研究凝聚态结构的简单、有效的方法.其中分形维数可用以表征溶液中凝聚体的形状和尺寸.因此, 非常适用于研究高分子溶液的聚集行为.

  4.1   凝聚态结构的研究

  一般可以通过静态光散射法(SLS), 利用公式(3)得到聚集体的分形维数d_f.这一参数反映了聚集体的形态和密实程度.通过分子链运动模式的变化, 可研究聚集态形成的动力学演变过程以及影响因素.

  指数规律已用于不同类型高分子溶液的聚集体研究, 如天然高分子凝胶、嵌段聚合物自组装聚集、共轭聚合物凝胶等^[49～54]. de Spirito等^[49]利用指数律研究了纤维蛋白、纤维凝胶在缓冲溶液中形态结构随Cl^－的变化过程.发现随着Cl^－浓度增加, 分形维数从1增加到1.8, 证明聚集体随着离子浓度的增加变得越来越膨胀、疏松(随分形维数增大, 分子链凝聚的密实程度提高).董宝中等^[24]利用小角X射线散射法研究了两亲性嵌段聚合物PSm-b-PVBAn的聚集行为(如图 10所示), 发现质量分形维数D_m随着溶剂改变从2.12增加到2.47, 表明聚集从溶胀线团变成相当密实的盘状结构.而表面分形维数D_s从2.98降至2.58, 证明聚集体的表面积由粗糙变平滑; 而再加入CoCl₂之后分形维数明显增大, 证明聚集体逐渐收缩成密实、且表面粗糙的二维盘状结构.陈信龙等^[50]和Knaapila等^[22]利用小角中子散射法(SANS)证明了共轭类聚合物DP6-PPV和三嵌段聚合物PF/PANI11112-b-PANI11在溶液中的聚集(其分形维数d_f在2.2～2.7和2.2～2.8之间)为网状结构. Bauer等^[51]则用SANS研究了碳纳米管聚集, 发现其聚集体的分形维数d_f＝2.5. Callejas-Fernández等^[52]则利用光散射法表征了聚乙烯基己内酰胺(PVCL)在水中形成的纳米颗粒凝胶, 得到这种纳米颗粒是外壳粗糙、平均分形维数为2.5、内核密度分布均匀的核-壳型球体结构. Muthukumar等^[53]利用光散射研究了聚电解质聚磺苯乙烯的钠盐NaPSS在BaCl₂溶液中相分离的过程, 发现单链的分形维数d_f是5/3, 说明单链呈现伸展的链构象; 而聚集体的分形维数d_f是3.5, 表明其分子链排列、堆砌的较密实.以上研究充分证明:指数律是适用于各种高分子聚集形态研究的理论工具.

  图 10  两亲性嵌段聚合物PS₆₈-b-PVBA₃₈在不同溶剂条件下的SAXS图, 横坐标I(h)是散射强度, 纵坐标h是散射矢量.后半段的曲线斜率代表了聚集体的幂指数 Figure 10.  SAXS curves of amphiphilic block copolymer PS₆₈-b-PVBA₃₈ in methanol, ethanol and isopropanol solvent.I(h)is the scattering intensity and h is the scattering vector. The right half of the curve slope represents the power index of aggregation^[24]

  图选项

  下载全尺寸图像

  下载幻灯片

  4.2   凝聚态结构动力学过程的研究

  凝聚态动力学过程的研究, 对认识其动力学演变过程及规律、实现对凝聚态结构调控、从高分子本征性质上提高材料与器件性能意义重大.人们对于高分子的聚集过程研究已有很多报道, 并提出了很多模型.但到目前为止, 最被认可的理论模型有两种: DLCA(扩散限制聚集模型)^[55～57]与RLCA(反应限制聚集模型)^[58～61].在DLCA过程中, 扩散运动是聚集的唯一限制条件.这一模型假设粒子之间没有排斥作用, 粒子之间的每一次碰撞都会导致不可逆的相互黏附.因此, 这一碰撞过程往往会形成较为疏松的聚集形态; 而在RLCA模型中, 由于粘附几率比较小, 以至于粒子之间要碰撞很多次才能相互黏附.因此粒子有更多机会填充进聚集之中, 这一模型下产生的聚集往往会更加密实.这两个过程形成的聚集形状均可用分形维数这一特殊指数来描述. RLCA过程的标志性分形维数α在2.1～2.2之间^[61], 而DLCA过程的分形维数为1.7～1.8, 而且在聚集过程中聚集的流体力学半径R_h与时间t存在指数关系: R_h∝t^α, 其中α < 1^[55].因此, 通过测定高分子溶液中聚集体的分形维数, 可描述高分子溶液中聚集的形成过程, 从而推断凝聚态结构的形成机理.

  此方面研究已经有很多报道^[62～68].严大东等^[62]发现间同立构甲基聚丙烯酸甲酯(s-PMMA)在θ温度以下的聚集分形维数为2.1, 符合RLCA过程.而吴奇等^[63]的研究发现, 嵌段聚合物聚丙烯酸-b-聚甲基丙烯酸甲酯(PAA-b-PNIPAM)在Ca^2＋和加热情况下的聚集过程符合DLCA模型.更多研究发现, 溶液中的聚集方式是可以调控的, 如Kumagai等^[64]的研究发现, 通过调节溶液的温度和pH, 便可使牛血清蛋白(BSA)在溶液中的聚集方式发生改变(如图 11所示).改变溶液环境, 如离子浓度/种类、温度、pH等条件都可能使溶液中的聚集过程发生改变而发生DLCA和RLCA的相互转化^[64～68], 这说明高分子的聚集过程是随环境变化的.因此, 在特定环境下的凝聚过程研究非常必要.依据指数规律, 我们可以认识不同条件下高分子凝聚态的形成机理, 从而调控聚集态结构动力学演变过程, 获得我们期望的材料性能.

  图 11  牛血清蛋白(BSA)溶液在不同pH和加热时间条件下的散射强度I(q)与散射矢量q的双对数图. (a)聚集的分型维数d_f大概为2.11, 属RLCA过程; (b)聚集的d_f约为1.8, 属DLCA过程 Figure 11.  Double logarithmic plot of scattered sight intensities I of BSA solutions heated for various times t_a against scattering vector q. (a) The fractal dimension of aggregation was about 2.11, which belongs to the RLCA process; (b) The fractal dimension of aggregation was about 1.8, which belongs to the DLCA process^[64]

  图选项

  下载全尺寸图像

  下载幻灯片

  5   结论与展望

  高分子的物理性质是呈非线性的.基于高分子链非线性特征, 利用指数规律(包括标度律)去深刻认识高分子的本征性质、运动规律, 单链、凝聚态相转变动力学过程与机理意义重大.随着越来越多功能高分子材料被开发利用, 对其基本物理性质的认识尤为重要.而指数律不失为一种简便、有效的理论工具.

  然而, 近十几年来, 基于高分子溶液中分子链本征性质的基础研究仍不多见; 大部分工作集中于高分子材料合成表征与提高器件性能, 鲜有从前体溶液的本征性质切入的深入研究.加之已有的标度律理论本身是基于单链, 尚缺少在聚集态方面的理论支撑而主要由经验公式代替.对此, 亟待完善与创建.加强高分子溶液的基础研究将是未来的重要任务.

• 1. [1]

     吴其晔, 高分子凝聚态物理学, 科学出版社, 北京, 2012, pp. 32～44.Wu Q. Y.Polymer Condensed Matter Physics, Science Press, Beijing, 2012, pp. 32～44.

  2. [2]

     de Gennes P. E.Scaling Concepts in Polymer Physics, Cornell University Press, New York, 1985.

  3. [3]

     吴其晔, 中国塑料, 2013, 27(1), 1.Wu Q. Y.China Plastics 2013, 27(1), 1.

  4. [4]

     Robinson G., Ross-Murphy S. B., Morris, E R. Carbohydr. Res. 1982, 107, 17. doi: 10.1016/S0008-6215(00)80772-7

  5. [5]

     Teraoka I.Polymer Solutions: An Introduction to Physical Properties, John Wiley & Sons, Inc., New York, 2001, pp. 209～221.

  6. [6]

     Kato T., Okamoto T., Tokuya T., Takahashi A.Biopolymers, 1982, 21:1623. doi: 10.1002/(ISSN)1097-0282

  7. [7]

     Picton L., Bataille G., Muller G.Carbohydr. Polym., 2000, 42:23. doi: 10.1016/S0144-8617(99)00139-3

  8. [8]

     Picton L., Merle L., Muller G.Int. J. Polym. Anal. Ch., 1996, 2:103. doi: 10.1080/10236669608233900

  9. [9]

     Beaucage G.Phys. Rev. E, 2004, 70:031401.

  10. [10]

      Gelade E. T. F., Goderis B., de Koster C. G..; Meijerink N., van Benthem R. A.T. M. Macromolecules, 2001, 34:3552. doi: 10.1021/ma001266t

  11. [11]

      Scherrenberg R., Coussens B., Van Vliet P., Edouard G., Brackman J., De Brabander E.Macromolecules, 1998, 31:456. doi: 10.1021/ma9618181

  12. [12]

      Huber K., Witte T., Hollmann J., Keuker-Baumann S. J.Am. Chem. Soc., 2007, 129:1089. doi: 10.1021/ja063368q

  13. [13]

      Lages S., Michels R., Huber K.Macromolecules, 2010, 43:3027. doi: 10.1021/ma9027239

  14. [14]

      Carpinti M., Ferri F., Giglio M., Paganini E., Perini U.Phys. Rev. A, 1990, 42:7347. doi: 10.1103/PhysRevA.42.7347

  15. [15]

      Schärtl W.Light Scattering from Polymer Solutions and Nanoparticle Dispersions, Springer Laboratory, Berlin, 2007.

  16. [16]

      Raspaud E., Lairez D., Adam M., Carton J. P.Macromolecules, 1994, 27:2956. doi: 10.1021/ma00089a011

  17. [17]

      Peng S. F., Wu C.Macromolecules, , 2001, 34:6795. doi: 10.1021/ma010376c

  18. [18]

      Roe R. J.Methods of X-ray and Neutron Scattering in Polymer Science, Oxford, New York, 2000.

  19. [19]

      Higgins J. S., Benoit H. C.Polymers and Neutron Scattering, Oxford, New York, 1994.

  20. [20]

      Perahia D., Traiphol R., Bunz U. H.F. J. Chem. Phys., 2002, 117:1827. doi: 10.1063/1.1486215

  21. [21]

      Wang H., Zhou W., Ho D. L., Winey K. I., Fischer J. E., Glinka C. J., Hobbie E. K.Nano Lett., 2004, 4:1789. doi: 10.1021/nl048969z

  22. [22]

      Knaapila M., Garamus V. M., Almásy L., Pang J. S., Forster M., Gutacker A., Scherf U., Monkman A. P.J. Phys. Chem. B, 2008, 112:16415. doi: 10.1021/jp806763d

  23. [23]

      荣利霞, 魏柳禾, 董宝中, 洪新国, 李福绵, 李子臣, 中国物理, 2003, 12, 771. doi: 10.1088/1009-1963/12/7/313Rong L. X., Wei L. H., Dong B. Z., Hong X. G., Li F. M., Li Z. C.Chin. Phys., 2003, 12:771. doi: 10.1088/1009-1963/12/7/313

  24. [24]

      Auguin, D.;Gostan, T.;Delsuc, M.-A.; Roumestand, C.C.R.Chimie 2004, 7, 265. doi: 10.1016/j.crci.2003.10.017

  25. [25]

      Crutchfield, C.A.; Harris, D.J.J.Magn.Reson.2007, 185, 179. doi: 10.1016/j.jmr.2006.12.004

  26. [26]

      Auge S., Schmit P.-O., Crutchfield C. A., Islam M. T., Harris D. J., Durand E., Clemancey M., Quoineaud A. A., Lancelin J. M., Prigent Y., Taulelle F., Delsuc M. A.J. Phys. Chem. B, 2009, 113:1914. doi: 10.1021/jp8094424

  27. [27]

      Chari K., Antalek B., Minter J.Phys. Rev. Lett., 1995, 74:3624. doi: 10.1103/PhysRevLett.74.3624

  28. [28]

      吴其晔, 高分子物理学, 高等教育出版社, 北京, 2011, pp. 17～24.Wu Q. Y.Polymer Physics, Higher Education Press, Beijing, 2011, pp. 17～24.

  29. [29]

      Roubroeks J. P., Mastromauro D. I., Andersson R., Christensen B. E., Åman P.Biomacromolecules, 2000, 1:584. doi: 10.1021/bm000017+

  30. [30]

      Sato T., Norisuye T., Fujita H.Macromolecules, 1984, 7:6.

  31. [31]

      Li W., Cui S. W., Wang Q.Biomacromolecules, 2006, 7:446. doi: 10.1021/bm050625v

  32. [32]

      Tao Y. Z., Zhang L. N., Yan F., Wu X. J.Biomacromolecules, 2007, 8:2321. doi: 10.1021/bm070335+

  33. [33]

      Huang Z. P., Huang Y. N., Li X. B., Zhang L. N.Carbohydr. Polym., 2009, 78:596. doi: 10.1016/j.carbpol.2009.05.027

  34. [34]

      Li S., Huang Y., Wang S., Xu X. J., Zhang L. N.J. Phys. Chem. B, 2014, 118:668. doi: 10.1021/jp4087199

  35. [35]

      Voit B. I., Albena L.Chem. Rev., 2009, 109:5924. doi: 10.1021/cr900068q

  36. [36]

      Mori H., Müller A. H. E., Simon P. F.W. In Macromolecular Engineering: Precise Synthesis, Materials Properties, Applications, Vol. 2, Eds.: Matyjaszewski K., Gnanou Y., Leibler L., Wiley-VCH, Weinheim, Germany, 2007 p.973.

  37. [37]

      Turner S. R., Voit B. I., Mourey T. H.Macromolecules, 1993, 26:4617. doi: 10.1021/ma00069a031

  38. [38]

      Mourey T. H., Turner S. R., Rubinstein M., Fréchet J. M. J., Hawker C. J., Wooley K. L.Macromolecules, 1992, 25:2401. doi: 10.1021/ma00035a017

  39. [39]

      Tomalia D. A., Hedstrand D. M., Wilson L. R.In Encyclopedia of Polymers Science, 2nd ed., Wiley, New York, 1990.

  40. [40]

      Isaacson J., Lubensky T. C.J. Phys. Lett., 1980, 41:469. doi: 10.1051/jphyslet:019800041019046900

  41. [41]

      Daoud M., Joanny J. F.J. Phys. (Les Ulis, Fr.), , 1981, 42:1359. doi: 10.1051/jphys:0198100420100135900

  42. [42]

      Flory P. J.Principles of Polymer Chemistry, Cornell University, Press, Ithaca, New York, 1953.

  43. [43]

      Luca E. D., Richards R. W., Grillo I., King S. M.J. Polym. Sci. Polom. Phys., 2003, 41:1352. doi: 10.1002/(ISSN)1099-0488

  44. [44]

      Ioan C. E., Aberle T., Burchard W.Macromolecules, 2000, 33:5730. doi: 10.1021/ma000282n

  45. [45]

      Hanselmann R., Burchard W., Lemmes R., Schwengers D.Macromol. Chem. Phys., 1995, 196:2259. doi: 10.1002/macp.1995.021960715

  46. [46]

      Huang L., Zhang L. L., Huang X. N., Li T., Liu B., Lu D. J.Phys. Chem. B., 2014, 118:791. doi: 10.1021/jp406598x

  47. [47]

      Knaapila M., Almásy L., Garamus V. M., Ramosd M. L., Justino L. L. G., Galbrecht F., Preis E., Scherf U., Burrowsd H. D., Monkmanm A. P.Polymer, 2008, 49:2033. doi: 10.1016/j.polymer.2008.02.046

  48. [48]

      Papi M., Arcovito G., de, Spirito. M..; Amiconi G.., Bellelli A., Boumis G.Appl. Phys. Lett., 2005, 86:183901. doi: 10.1063/1.1915526

  49. [49]

      Li Y.C, Chen K.B, Chen H. L., Hsu C. S., Tsao C. S., Chen J. H., Chen S. A.Langmuir, 2006, 22:11009. doi: 10.1021/la0612769

  50. [50]

      Bauer B. J., Hobbie E. K., Becker M. L.Macromolecules, 2006, 39:2637. doi: 10.1021/ma0527303

  51. [51]

      Callejas-Fernández J., Ramos J., Forcada J., Moncho-Jordá A. J.Colloid Interface Sci., 2015, 450:310. doi: 10.1016/j.jcis.2015.03.031

  52. [52]

      Kanai S., Muthukumar M. J.Chem. Phys., 2007, 127:25.

  53. [53]

      Dai S., Tam K. C., Jenkins R. D.Macromolecules, 2000, 33:404. doi: 10.1021/ma990887n

  54. [54]

      Witten T. A., Sander L. M.Phys. Rev. Lett., 1981, 47:1400. doi: 10.1103/PhysRevLett.47.1400

  55. [55]

      Witten T. A., Sander L. M.Phys. Rev. B, 1983, 27:5686. doi: 10.1103/PhysRevB.27.5686

  56. [56]

      Meakin P.Phys. Rev. Lett., 1983, 51:1119. doi: 10.1103/PhysRevLett.51.1119

  57. [57]

      Meakin P.Phys. Rev. A, 1990, 41:2005. doi: 10.1103/PhysRevA.41.2005

  58. [58]

      Meakin P.Adv. Colloid Interface Sci., 1988, 28:249.

  59. [59]

      Brown W. D., Ball R. C.J. Phys. A, 1985, 18:517. doi: 10.1088/0305-4470/18/9/006

  60. [60]

      Vicsek T.Fractal Growth Phenomena, World Scientific, London, 1992.

  61. [61]

      Chen W. N., Zhao Y., Jiang Y., Yan D. D., Han C. C.ChemPhysChem, 2004, 5:1745. doi: 10.1002/(ISSN)1439-7641

  62. [62]

      Liu X. B., Luo S. K., Ye J., Wu C.Macromolecules, 2012, 45:4830. doi: 10.1021/ma300629d

  63. [63]

      Hagiwara T., Kumagai H., Nakamura K.Biosci. Biotech. Biochem., 1996, 60:1757. doi: 10.1271/bbb.60.1757

  64. [64]

      Lin W., Zhou Y. S., Zhao Y., Zhu Q. S., Wu C.Macromolecules, 2002, 35:7407. doi: 10.1021/ma020372n

  65. [65]

      Liao W., Zhang Y. J., Guan Y., Zhu X. X.Langmuir, 2012, 28:10873. doi: 10.1021/la3016386

  66. [66]

      Burns J. L., Yan Y. D., Jameson G. J., Biggs S.Langmuir, 1997, 13:6413. doi: 10.1021/la970303f

  67. [67]

      Li, N.;Li, Y.B.; Wang, X.G.Macromolecules 2011, 44, 8598. doi: 10.1021/ma200992n

• 

  图 1  通过高分子稀溶液中黏均分子量M_η和特性黏度[η]之间的双对数图, 得到Mark-Houwink指数α

  Figure 1  The Mark-Houwink index α was obtained from the double logarithmic plot of intrinsic viscosity [η] against viscosity-average molecular weight M_η^[4]

  下载: 全尺寸图片 幻灯片
  

  图 2  重均分子量M_w和均方根回转半径R_g( < s² > ^1/2)之间的指数关系

  Figure 2  Exponential relationship between the root mean square radius of gyration R_g ( < s² > ^1/2) and weight-average molecular weight M_w^[6]

  下载: 全尺寸图片 幻灯片
  

  图 3  静态光散射(SLS)表征光强函数I(q)和散射矢量q之间的指数关系

  Figure 3  Exponential relationship between the excess scattering intensity I(q) and the scattering vector q by static light scattering (SLS)^[17]

  下载: 全尺寸图片 幻灯片
  

  图 4  小角中子散射法中光强函数I(q)和散射矢量q之间的指数关系

  Figure 4  Exponential relationship between the excess scattering intensity I(q) and the scattering vector q by small angle neutron scattering (SANS)^[22]

  下载: 全尺寸图片 幻灯片
  

  图 5  核磁共振法中扩散系数D与重均分子量M_w之间的指数关系

  Figure 5  Exponential relationships between the diffusion coefficient (D) and the weight-average molecular weight M_w via the nuclear magnetic resonance (NMR)^[25]

  下载: 全尺寸图片 幻灯片
  

  图 6  (a)小麦β-葡聚糖在0.5 mol/L的NaOH溶液中特性黏度[η]的对数与重均分子量M_w之间的指数关系图. (b)小麦β-葡聚糖在0.5 mol/L的NaOH溶液中均方根回旋半径R_g的对数与重均分子量M_w之间的指数关系图

  Figure 6  (a) Double logarithmic plot of [η] against M_w of wheat β-glucan in 0.5 mol/L NaOH solution. (b) Double logarithmic plot of the molecular weight M_w vs the radius of gyration R_g of wheat β-glucan in 0.5 mol/L NaOH solution^[32]

  下载: 全尺寸图片 幻灯片
  

  图 7  (a)水溶性多聚糖(TM3a)在0.25 mol/L的LiCl/DMSO溶液中均方根回旋半径 < s² > ^1/2(R_g)的对数与重均分子量M_w之间的指数关系图. (b)水溶性多聚糖(TM3a)在0.25 mol/L的LiCl/DMSO中特性黏度[η]的对数与重均分子量M_w之间的指数关系图

  Figure 7  (a) Plot of log < s² > ^1/2(R_g) vs log M_w for TM3a in 0.25 mol/L LiCl/DMSO. (b) Double logarithmic plot of [η] against M_w of TM3a in 0.25 mol/L LiCl/DMSO^[33]

  下载: 全尺寸图片 幻灯片
  

  图 8  由SEC和黏度测定联用装置测定的两种超支化聚酯的特性黏度[η]的对数与重均分子量M_w之间的指数关系图

  Figure 8  Plot of log [η] vs log [M_w] for two kinds of hyperbranched polyester as obtained from size-exclusion chromatography (SEC) & viscosity determination device^[38]

  下载: 全尺寸图片 幻灯片
  

  图 9  由散射数据得到的光强I(q)与散射矢量q之间的指数关系, 得到PF衍生物在甲苯溶液中的结构: (a)有交联点的网状结构; (b)高斯线团转变的棒状粒子(设想I)或者有节点的网状结构(设想II); (c)完全溶解的棒状结构(实质是单链)

  Figure 9  Schematic description of the scattering data and proposed structures of PFs in toluene: (a) a network-like structure with cross-linked nodes; (b) a structure of rodlike particles forming Gaussian coils (scenario I) or sheet-like aggregates (scenario II) in the longer length scales, and (c) a structure of fully dissolved rod like particles (essentially single polymer chains)^[48]

  下载: 全尺寸图片 幻灯片
  

  图 10  两亲性嵌段聚合物PS₆₈-b-PVBA₃₈在不同溶剂条件下的SAXS图, 横坐标I(h)是散射强度, 纵坐标h是散射矢量.后半段的曲线斜率代表了聚集体的幂指数

  Figure 10  SAXS curves of amphiphilic block copolymer PS₆₈-b-PVBA₃₈ in methanol, ethanol and isopropanol solvent.I(h)is the scattering intensity and h is the scattering vector. The right half of the curve slope represents the power index of aggregation^[24]

  下载: 全尺寸图片 幻灯片
  

  图 11  牛血清蛋白(BSA)溶液在不同pH和加热时间条件下的散射强度I(q)与散射矢量q的双对数图. (a)聚集的分型维数d_f大概为2.11, 属RLCA过程; (b)聚集的d_f约为1.8, 属DLCA过程

  Figure 11  Double logarithmic plot of scattered sight intensities I of BSA solutions heated for various times t_a against scattering vector q. (a) The fractal dimension of aggregation was about 2.11, which belongs to the RLCA process; (b) The fractal dimension of aggregation was about 1.8, which belongs to the DLCA process^[64]

  下载: 全尺寸图片 幻灯片

  表 1  Mark-Houwink指数α值对应的分子链形状

  Table 1.  The molecular chain shape corresponding to the value of Mark-Houwink index α

  Mark-Houwink index α	0.33	0.5～0.6	1.0
  分子链形状	球状	柔性无规线团	棒状

  下载: 导出CSV
•