
QSAR Models for Predicting Additive and Synergistic Toxicities of Binary Pesticide Mixtures on Scenedesmus Obliquus
English
QSAR Models for Predicting Additive and Synergistic Toxicities of Binary Pesticide Mixtures on Scenedesmus Obliquus
-
Key words:
- pesticide
- / QSAR
- / toxicity prediction
- / binary mixture
- / algae
-
1. INTRODUCTION
In recent years, with the improvement of agricultural science and technology and the increase of agricultural inputs, pesticides play a great role in agrarian cultivation, such as improving crop yield[1]. The threats posed to the environmental quality of agricultural soils and surface water cannot be ignored. Studies have shown that nonpoint source pollution is the leading cause of surface water pollution globally, with the largest contribution from agricultural point source pollution. Pesticide loss and residual pollution caused by the heavy application of pesticides, which causes the environmental pollution of soil and water in agricultural fields, have become an increasingly prominent ecological problem[2, 3]. For example, Zheng et al.[4] detected 82 pesticide residues in the Chiu-lung Rive of Fujian Province, China. Canccapa et al.[5] found high detection rates of chlorpyrifos, diazinon, and carbendazim in the Turia and JúcarRivers (Spain) from 2010 to 2013, respectively. Xu et al.[6] reported the results of pesticide residue monitoring from 55 main water sources in 12 urban areas of Yantai City: organophosphorus and pyrethroid pesticides were detected in all water sources at concentrations ranging from 103.0 to 345.7 ng/L. Therefore, it is of great significance to study the pollution and ecological risk of pesticide exposure to the environment.
Algae play an essential role in aquatic and soil ecosystems. Algae can carry out photosynthesis, and the characteristics of their species can directly affect the structures and functions of aquatic ecosystems, which has been used as indicator organisms in ecotoxicological research in recent years[7]. Many research achievements have been obtained. Tien et al.[8] studied the single toxic effects of chlorpyrifos, terbufos and methamidophos on diatoms, cyanobacteria and green algae. The results showed that different algae showed wide variation in sensitivity to different pesticides, with green algae being the most tolerant with EC50 of 1.29~41.16 mg/L. Wan et al.[9] investigated the toxicity of trichlorfon to the fresh-water alga Chlamydomonas reinhardtii, with an EC50 of 200 mg/L. Studies have shown that Chlamydomonas reinhardtii has a high tolerance ability to trichlorfon and is promising for removing trichlorfon from natural water environments. Liu et al.[10] studied the single and combined toxicities of six pesticides (simetryn, bromacil, hexazinone, dodine, propoxur, and metalaxyl) on Chlorella pyrenoidosa. With the concentration addition as an additive reference model, four kinds of binary mixture rays exhibited antagonistic effects on Chlorella pyrenoidosa. It is imperative to apply algae to the toxicity research of pesticide pollutants, and it is of great significance to evaluate the combined toxicity of pesticide pollutants for ecological risk.
There are many varieties of pesticides, and compound pesticides account for a large proportion. Mixed-use, blind use or abuse of multiple pesticides lead to the prominent phenomenon of multiple pesticide residues in the environment. This leads to the fact that pesticides in the environment will mix in many and varied forms, resulting in complex mixture systems[11]. It is possible that the components of these complex mixtures produce toxic interactions with each other or are enriched in living organisms, causing more serious environmental pollution problems. Therefore, the investigation of combined toxic effects of pesticides has become the focus of researchers in recent years. Tien et al.[8] studied the combined toxicity of chlorpyrifos, terbufos and methamidophos on diatoms, cyanobacteria and green algae. The results indicated that the mixtures of pesticides exhibited antagonism and synergism to algae, and pesticide mixtures are more likely to induce detoxification mechanisms than single pesticides. Du et al.[12] used plasma metabolomics to evaluate the toxic effects of four organophosphorus pesticides (dichlorvos, acephate, dimethoate and phorate) on male Wistar rats. The results showed that the combination of the four drugs could produce a combined effect at a non-damaging effect level, causing body oxidative stress and liver and kidney dysfunction.
Quantitative structure-activity relationship (QSAR) is a method that can effectively predict the physicochemical properties, environmental behavior, and toxicity characteristic effect parameters of organic pollution[13]. The qualitative identification of the combined effect of mixtures has achieved remarkable results. Qualitative research can determine that the combined effect of mixtures is antagonism, synergism or additive[14, 15], which has been widely used. However, this qualitative discrimination cannot quantitatively determine the intensity of toxicity, so the research on combined toxicity must be changed from qualitative research to quantitative research. QSAR is one of the commonly used methods to study the combined toxicity of mixtures quantitatively, and it is also the frontier and emphasis of current structural-activity relationship research[16]. In this study, we selected the green algae Scenedesmus obliquus (S. obliquus) as target organisms and determined the toxicities of five pesticides, including two herbicides (linuron and metribuzin) and three insecticides (dimethoate, dichlorvos and trichlorfon). Based on the single toxicity of five pesticides and the combined toxicity of seven binary mixture systems designed by direct equipartition ray (EquRay)[17], as well as screening the optimal descriptors describing the contributions of these five pesticides to the combined toxic effect, QSAR models that could accurately predict the toxic value of binary mixtures were developed. Therefore, the model may serve as a theoretical basis for predicting the binary toxicities of pesticide compounds.
2. MATERIALS AND METHODS
2.1 Test organism and culture
The insecticide and herbicide are used in agricultural areas to protect crops and control pests and weeds. Linuron and metribuzin belong to herbicides, and dimethoate, dichlorvos and trichlorfon belong to insecticides, and are widely used in agricultural production[18]. However, in practical use, their actual utilization is very low, and a large amount of the residual herbicides and insecticides enter into the ecosystem such as soil and water bodies[19], which pose a serious threat to the ecological environment and even human health. Researchers have paid great attention to the pollution of herbicides and insecticides to the environment[20], but there are few reports on their mixtures' toxic effects. Five pesticides including linuron (CAS 330-55-2, purity > 99.44%), dimethoate (CAS 60-51-5, purity > 99.30%), dichlorvos (CAS 62-73-7, purity > 99.62%), trichlorfon (CAS 52-68-6, purity > 97.20%), and metribuzin (CAS 21087-64-9, purity > 99.82%) were purchased from Dr Ehrenstorfer GmbH Co.. The S. obliquus was purchased from Freshwater Algae Culture Collection at the Institute of Hydrobiology (FACHB), numbered FACHB-5.
2.2 Toxicity test and concentration-response curve fitting
A modified procedure of the microplate toxicity analysis (MTA) based on algae growth inhibition was used to determine the toxicity of a pesticide or a mixture to S. obliquus[21]. In the MTA, the peripheral wells were filled with 200 μL water to minimize the edge effects. A total of 24 wells of the second, sixth, seventh, and eleventh columns in a 96-well microplate were selected as blank controls, and the remaining 36 microwells were designed with twelve concentration gradients of three parallels by a dilution factor. A total of 100 μL algal liquid was added to each well, and the total volume was 200 μL. Three plates were repeated and incubated at 25 ℃ with a light: dark ratio of 12:12. The optical density (OD) of S. obliquus was determined on the Power Wave microplate spectrophotometer (American BIO-TEK Company) after 96 h at the wavelength of 690 nm. The toxicity is expressed in terms of inhibition rate (E), and the formula is given in Eq. (1).
$ E=\left(1-\frac{OD}{{OD}_{0}}\right)\times 100\% $ (1) where OD was the average optical density of the experimental group and OD0 was that of the control group.
To obtain the effect value and effect concentration for individual pesticide or their mixtures, Logit (Eq. 2) and Weibull (Eq. 3) functions were used to fit the concentration-response curve (CRC) measured by MTA with the nonlinear leastsquares method. In statistics, the ratio of the number of data points (i. e., the number of samples) to the model parameters should be greater than 5:1. There were 12 concentration points in the MTA. Therefore, the two-parameter equation (Logit and Weibull) was used to fit the curve in this study, which could effectively reduce the over-fitting phenomenon. The coefficient of determination (R2) is an evaluation index of the final fitting regression effect. For each CRC, Logit and Weibull functions were used to fit the curve simultaneously, and then their R2 was compared. The closer R2 is to 1, the better the fitting regression effect is.
$ E=1/(1+\mathrm{e}\mathrm{x}\mathrm{p}(-\alpha -\beta \mathrm{l}\mathrm{o}\mathrm{g}c\left)\right) $ (2) $ E=1-\mathrm{e}\mathrm{x}\mathrm{p}(-\mathrm{e}\mathrm{x}\mathrm{p}(\alpha +\beta \mathrm{l}\mathrm{o}\mathrm{g}c\left)\right) $ (3) where E is the toxic effect value, c the concentration dose, α the positional parameter, and β the slope parameter.
2.3 Mixture design
To systematically examine the variation of toxicity in mixtures, five mixtures ray with different concentration ratios (pi, i = 1, 2, 3, 4, 5) were designed by direct equipartition ray design (EquRay) for every group mixture (pi, Table 2), and 12 concentration points were arranged for each ray. The concentration ratio (pi) of a component (pesticide) is defined as a ratio of the concentration of the component in a mixture to the sum of concentrations of all components in the mixture. There are seven groups of binary mixtures, B1 consisting of linuron and dimethoate, B2 of linuron and dichlorvos, B3 of linuron and trichlorfon, B4 of dichlorvos and trichlorfon, B5 of dichlorvos and metribuzin, B6 of trichlorfon and metribuzin and B7 of dimethoate and metribuzin.
2.4 Toxic interaction analysis of the mixtures
The concentration addition (CA) model was used as the additive reference model to analyze and compare the toxic interactions in different concentration ranges from CRCs of mixtures. The formula of the CA model is expressed as in the following equation[22]:
$ EC{x}_{mix}={\left({\sum }_{i}^{n}\frac{{p}_{i}}{EC{x, }_{i}}\right)}^{-1} $ (4) where ECxmix is the mixture concentration in x% combined effect, n is the number of mixture components, ECx, i represents the concentration at which the effect (x%) produced in the presence of the ith compound alone in the mixture, and pi is the concentration ratio of the ith component in the mixture.
The combined toxic interaction of mixture was qualitatively distinguished by comparing experimental CRC with predictive CRC by CA in the whole effect range[23]. Due to the experimental error in the toxicity experiment and the fitting error in the nonlinear fitting of CRC, 95 percent observed confidence intervals (OCI) of CRC must be considered to compare the predictive CRC by CA with the experimental CRC. The predictive CRC by CA is almost located between the upper limit and lower one of the 95 percent OCI, which states that the toxicities of the mixtures are additive. The predictive CRC by CA significantly deviates from the experimental CRC, locating above the 95 percent OCI and exhibiting antagonistic interaction. The predictive CRC by CA significantly deviates from the experimental CRC, locating under the 95 percent OCI and displaying synergistic interaction.
2.5 Characterization of molecular structure of mixtures
Firstly, 3D molecular structures of five single pesticides and their binary pesticide mixtures were pre-optimized for energy minimization of Guassian09 software[24]. Secondly, density functional theory (DFT) of Guassian09 software at the B3LPY/6-31G (d, p) level was employed to optimize the molecular structure of single and binary mixed pesticides to the best transition state[24]. Sixteen descriptors were extracted, including polarizability, single-point energy, dipole moment, the most positive charge, the most negative charge, EHOMO, ELUMO, zero vibration energy, enthalpy of formation, Gibbs free energy, heat correction value, constant volume molar melting, entropy, absolute hardness, softness, and chemical potential. Thirdly, the AM1 method which runs the MOPAC program was used to calculate eight descriptors of molecular structures of single and binary mixed pesticides, including the final formation heat, total energy, electron energy, core repulsion, COSMO surface area, COSMO volume, ionization potential and molecular weight[25]. Finally, Dragon software[26] can only calculate the molecular descriptors of a single pesticide, including topological index, connection index, RDF descriptor, 3D-MoRSE descriptor, and edge adjacency index. A total of 5270 single pesticide molecular structure descriptors are screened preliminarily in dragon software, and the remaining 43 qualified descriptors are obtained.
If the binary mixture conforms to the concentration addition model, it can be considered that the mixture has no interaction, which can be characterized by the mixture descriptor (xmix) as follows[27]:
$ {x_{mix}} = {p_1}{x_1} + {p_2}{x_2} + \cdot \cdot \cdot + {p_i}{x_i} $ (5) where xmix is mixture descriptors, xi represents a descriptor for component, and pi is the concentration ratio of the ith component in the mixture.
If the components contained in the mixture are considered together as a whole, and molecular structure descriptors of all components in the mixture are calculated simultaneously by Guassian09 and MOPAC software, a mixture descriptor with interaction information can be obtained as below:
$ {x_{mix}} = ({p_1}{x_1} + {p_2}{x_2} + \cdot \cdot \cdot + {p_i}{x_i}) - n{x_m} $ (6) where xmix is the mixture descriptors, xi represents a descriptor for component, pi is the concentration ratio of the ith component in the mixture, n is the number of components of the mixture and xm is the descriptor obtained when the mixture is calculated as a whole.
2.6 Establishment and validation of the QSAR model
The overall data set is randomly divided into a training set (70%) and a test set (30%) in QSARINS software[28, 29]. The test set is used for external validation of the model. The best descriptor based on genetic algorithms was selected in QSARINS software and QSAR models were built with training set by multiple linear regressions (MLR). To ensure the reliability and validity of the regression model, the leave-one-out cross-validation (LOO), leave-many-out cross-validation (LMO), y-randomization test, and the bootstrapping method are used for the internal validation.
The application domain (AD) of the QSAR model is a thoretical area in the space defined by the descriptors used in the model, and established QSAR models should make predictions about the reliability of that space, defining the AD of the QSAR model with a leverage value hi, which is calculated as[30]:
$ h_{i} = x_{i}·(X^{T}X)^{-1}·x_{i}^{T} (7) $ (7) where xi represents the original variable of molecular descriptor for a compound and X is the descriptor matrix of the compounds of the training set.
3. RESULTS AND DISCUSSION
3.1 Toxicity of five pesticides to S. obliquus
The fitted CRCs parameters (α and β), fitted statistics (R2 and RMSE), and EC(10, 30, 50) of five pesticides are listed in Table 1. From Table 1, apart from the CRCs of dimethoate and dichlorvos depicted by the Weibull function, the CRCs of the other three pesticides to S. obliquus can be well described by the Logit function (R2 > 0.9704 and RMSE < 0.0783). The experimental concentration-toxicity (inhibition percent) data points and fitted CRCs are shown in Fig. 1. The EC50 value is considered as a toxicity index, and the toxicity order of five pesticides to S. obliquus was metribuzin > linuron > dichlorvos > trichlorfon > dimethoate. The freshwater green algae S. obliquus was more sensitive to two herbicides (linuron and metribuzin) than the insecticide. The structures of dimethoate, dichlorvos, and trichlorfon have a similar frame-work, except that the side chain substituents are different, and the toxicities of dichlorvos and trichlorfon containing chlorine substituents were slightly greater than that of dimethoate without chlorine substituents. Therefore, the side-chain chlorine substituents of pesticide molecules may enhance their toxicity. In contrast, metribuzin is close to and has a cyclic structure to linuron, and its toxicity is higher than that of dimethoate, dichlorvos, and trichlorfon, so the cyclic structure of pesticide molecules may increase their toxicity.
Table 1
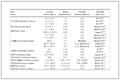 Table 1. Fitted CRC Parameters (α and β), Fitted Statistics (R2 and RMSE), and EC(10, 30, 50) of Five Pesticides
Table 1. Fitted CRC Parameters (α and β), Fitted Statistics (R2 and RMSE), and EC(10, 30, 50) of Five PesticidesPesticide CAS RN F α β RMSE R2 EC50 EC30 EC10 Linuron 330-55-2 L 27.33 3.90 0.0607 0.9899 9.824E-08 5.957E-08 2.685E-08 Dimethoate 60-51-5 W 6.39 2.28 0.0605 0.9808 9.304E-04 5.562E-04 1.623E-04 Dichlorvos 62-73-7 W 6.26 2.16 0.0528 0.9704 7.252E-04 4.213E-04 1.148E-04 Trichlorfon 52-68-6 L 14.48 4.66 0.0783 0.9713 7.811E-04 5.139E-04 2.638E-04 Metribuzin 21087-64-9 L 29.87 4.17 0.0524 0.9809 6.870E-08 4.303E-08 2.042E-08 F: fitted functions where L refers to Logit function and W to Weibull function; α and β are fitting function parameters;
CAS RN is the chemical abstracts service register number; R2 and RMSE are the fitting function statistic.Figure 1
3.2 Combined toxicity of pesticide mixtures
Using the MAT method to determine the toxicity of 35 rays of pesticide binary mixture to S. obliquus, the experimental concentration-toxicity (inhibition percent) data points and fitted CRCs are shown in Fig. 2. The CRCs of two rays (B1-R1 and B3-R5) of 35 mixture rays can be well described by Logit (L) functions and the other 33 rays can be described by Weibull (W) functions (Table 1S). The fitted regression coefficients (α and β) and statistics, determination coefficient (R2) and root mean squared error (RMSE) as well as pEC(50, 30, 10) are listed in Table 1S. It has been shown that 35 mixture rays exhibit a good statistical significance with the determination coefficient of > 0.93 and the root mean squared error of < 0.1254, which explains that all pesticide mixtures have a good concentration-response relationship.
Figure 2
3.3 Toxicity interaction between pesticide mixtures
Selecting CA as an additive reference model, if the experimental fitting effect is higher, equal to or lower than the CA prediction effect, the mixture exhibits synergistic, additive and antagonistic interactions. From Fig. 2, at different concentration proportions, the fitted CRCs deviated from CA predicted line to different degrees, i.e., the different interactions.
The predictive CRCs by CA of five binary mixture rays, B3-R1, B3-R2, B7-R2, B7-R3 and B7-R5, significantly deviated from the experimental CRCs, locating under the 95 OCI and displaying synergistic interactions. The predictive CRCs by CA of ten binary mixture rays, B3-R3, B3-R4, B3-R5, B5-R1, B5-R2, B5-R3, B5-R4, B5-R5, B7-R1, and B7-R4, evidently deviated from the experimental CRCs in high concentration area (including EC50 and EC30), locating under the 95 percent OCI and showing high concentration synergistic interactions. The predictive CRC by CA of B6-R1 clearly deviated from the experimental CRC in the medium concentration zone (including EC10), locating under the 95 percent OCI and exhibiting medium concentration synergistic interactions. The predictive CRC by CA of B2-R1 obviously deviated from the experimental CRC in the low concentration region, locating under the 95 percent OCI and demonstrating low concentration synergistic interactions. For the remaining 18 rays of 35 mixture rays, the predictive-CRCs were almost completely located between the upper limit and lower one of the 95 percent OCI, which states that the toxicities of the mixtures are additive. Furthermore, 16, 15, and 10 rays of mixtures displayed synergism at EC50, EC30 and EC10 concentration effects, respectively.
The CA model was used to evaluate the toxicity interaction (synergism or additive) of binary mixtures of pesticides. The results showed that the proportions of rays with synergistic effect were 46%, 43% and 29% at EC50, EC30 and EC10 concentrations, respectively. Therefore, the variation of concentration level may change the toxicity interaction of binary mixtures. Besides, from EC10 to EC50, the synergistic effect of pesticides on S. obliquus was enhanced with the increase of concentration level of a binary mixture. As previous studies have shown, synergy was enhanced at the high concentration level of binary mixtures such as pesticides and metals[31, 32].
3.4 QSAR model of pesticide mixtures
For genetic algorithm parameters, we selected the maximum population size (1000 chromosomes), the minimum mutation rate (0.05), the maximum model size (4 variables) and 500 as the number of generations. By selecting four descriptors as the best independent variables and using the pEC50, pEC30 and pEC10 (the negative logarithm of EC50, EC30 and EC10) values as dependent variables, the QSAR models of pesticide mixtures were established, including model pEC50, model pEC30 and model pEC10. The model pEC50 was shown as follows:
$ $ pEC_{50} = –(1681.399 ± 370.9857) + (0.0003 ± 0.0002)·{\bf{TE}} – (0.0049 ± 0.0012)·{\bf{COA}}\\ \;\;\;\;– (0.0357 ± 0.0102)·{\bf{DM}} + (3499.740 ± 772.6334)·{\bf{GGI4}} \\ {R^2} = 0.9403,RMSE = 0.1033,Q_{{\rm{LOO}}}^2 = 0.8921,Q_{{\rm{LMO}}}^2 = 0.8760,R_{{\rm{bstr}}}^2 = 0.9316,Q_{{\rm{bstr}}}^2 = 0.8858,R_{{\rm{yrand}}}^2 = 0.1070\\Q_{{\rm{yrand}}}^2 = - 0.4114,RMS{P_{{\rm{ext}}}} = 0.1420,Q_{{\rm{F}}1}^2 = 0.8890,Q_{{\rm{F}}2}^2 = 0.8291,Q_{{\rm{F}}3}^2 = 0.8872,CCC = 0.8985,F = 78.7920 $ (8) where, TE is the total energy, COA the cosmo area, DM the dipole moment, GGI4 the topological charge index of order 4, RMSE the root mean square error of the model, F the Fischer's statistic, R2 the coefficient of multiple determination, QLOO2 the correlation coefficient of leave-one-out cross-validation, and QLMO2 the correlation coefficient of leave-many-out cross-validation, Rbstr2 and Qbstr2 are the average correlation coefficient of bootstrapping method, Ryrand2 and Qyrand2 the maximum R2 and Q2 the values of the y-randomization tests, RMSPext is the root mean square error of test set, QF12, QF22 and QF32 are the external validation coefficient of the model, and CCC is the concordance correlation coefficient of the model. The values before and after "±" represent the regression coefficient of the model and its corresponding standard deviation.
The model pEC30 equation is as follows:
$pEC_{30} = –(1726.8388 ± 432.7641) + (0.003 ± 0.0002)·{\bf{TE}} – (0.0056 ± 0.0015)·{\bf{COA}} \\\;\;\;\;\; – (0.0366 ± 0.0123)·{\bf{DM}} + (3593.603 ± 901.8907)·{\bf{GGI4}} \\ {R^2} = 0.9298,RMSE = 0.1196,Q_{{\rm{LOO}}}^2 = 0.8780,Q_{{\rm{LMO}}}^2 = 0.8731,R_{{\rm{bstr}}}^2 = 0.9196,Q_{{\rm{bstr}}}^2 = 0.8630,R_{{\rm{yrand}}}^2 = 0.1051 \\ Q_{{\rm{yrand}}}^2 = - 0.4184,RMS{P_{{\rm{ext}}}} = 0.1440,Q_{{\rm{F}}1}^2 = 0.8361,Q_{{\rm{F}}2}^2 = 0.8159,Q_{{\rm{F}}3}^2 = 0.8906,CCC = 0.9177,F = 66.2390 $ (9) where, TE is the total energy, COA the cosmo area, DM the dipole moment, and GGI4 the topological charge index of order 4.
The model pEC10 is shown as below:
$ pEC_{10} = –(1914.501 ± 565.2238) + (0.0044 ± 0.0016)·{\bf{COA}} – (0.5269 ± 0.2981)·{\bf{MW}}\\ \;\;\;\;– (5.8414 ± 3.8905)·E_{HOMO} + (3985.4347 ± 1178.3972)·{\bf{GGI4}} \\{R^2} = 0.8564,RMSE = 0.1759,Q_{{\rm{LOO}}}^2 = 0.7615,Q_{{\rm{LMO}}}^2 = 0.7484,R_{{\rm{bstr}}}^2 = 0.8588,Q_{{\rm{bstr}}}^2 = 0.7679,R_{{\rm{yrand}}}^2 = 0.1272\\ Q_{{\rm{yrand}}}^2 = - 0.3807,RMS{P_{{\rm{ext}}}} = 0.1781,Q_{{\rm{F}}1}^2 = 0.8327,Q_{{\rm{F}}2}^2 = 0.8324,Q_{{\rm{F}}3}^2 = 0.8281,CCC = 0.9019,F = 29.8160 $ (10) where, COA is the cosmo area, MW the molecular weight, EHOMO the highest molecular orbital energy, and GGI4 the topological charge index of order 4.
The statistic is used to evaluate the internal and external predictive ability of QSAR models. If the statistic values are satisfied (thus the models are robust), the models are acceptable. Q2 greater than 0.5 considered the model to be good, and greater than 0.9 showed the model excellent[33]. Tropsha et al.[34] suggested that both R2 and Q2 are greater than 0.6. There was no significant difference between correlation coefficients of models pEC50 (R2 = 0.9403 and QLOO2 = 0.8321), pEC30 (R2 = 0.9298 and QLOO2 = 0.8780) and pEC10 (R2 = 0.8564 and QLOO2 = 0.7615), which shows these models have strong robustness. In addition, R2 – QLOO2 < 0.1[35], so the models have no over-fitting. Furthermore, the statistic values of QLMO2 and QLOO2 were close to each other, and the result of bootstrapping method[36] is as below: Rbstr2 > 0.6, Qbstr2 > 0.5, indicating that the models all have good robustness. The result of y-randomization test was Ryrand2 > Qyrand2[37], which demonstrates no chance correlation between the independent and dependent variables of the models. The external predictive ability of the model can be assessed with statistics of QF12, QF22 and QF32. All relevant statistical parameters of the external validation of the three models meet the conditions suggested by Chirico and Gramatica[38], in which all QF12, QF22, and QF32 shall be greater than 0.6 and the concordance correlation coefficient (CCC) should be greater than 0.85. It could be indicated that the three models have a good external predictive ability.
Williams plot is the relationship between LOO standard residual and leverage value[39], and the leverage threshold (h*) of models pEC50, pEC30 and pEC10 was 0.4800. The leverage threshold h* = 0.4800 was derived according to QSARMLR program, and the standard residual is the value obtained by dividing the residual by its standard deviation, setting at ± 2.5[40]. If the absolute value of the LOO standard residual of a sample is greater than 2.5 and greater than h*, the sample is abnormal[41]. Moreover, it could be seen from Fig. 3 that the calculated values of the training set and the predicted values of the test set are all within the application domain, indicating that the model has no abnormal samples and the data of all binary mixture rays are reliable.
Figure 3
3.5 Interpretation of the descriptors
GGI4 is defined as the sum of the corresponding charge terms absolute values over a pair of vertices (nonhydrogen atoms) with all topological distances equal to 4 in the molecule. Its value is mainly determined by the number of nonhydrogen atoms, the charge, and the topological distance. GGI4 can be calculated by establishing the compound matrix (distance matrix D, coulomb matrix T, matrix M = C⋅T, where C is the adjacency matrix). The mathematical model can be expressed as[42]:
$ {G_k} = \sum\limits_{i = 1}^{N - 1} {\sum\limits_{j = 1}^N {\left| {{g_{ij}}} \right|} } {\delta _{k, {d_{ij}}}} $ (11) where element dij of matrix D is the topological distance between atoms i and j, gij = mij – mji (mij is the matrix M element) denotes the difference in magnitude of net charge of atoms i to j, N is the number of nonhydrogen atoms in the molecule, k is an indicator variable for the topological distance between atoms i and j, taking values 1~10 k (k = 4 in this descriptor), δ is Kronecker delta[43], defined as two variables, i and j, which equals 1 when i = j and equals 0 when i is not equal to j.
The cosmo area is used in the cosmo model to characterize the size of the area where solvent molecules surround the molecules in solution[44]. Total energy includes electronic energy and nuclear repulsion energy, and its value is mainly related to the number of atoms in the molecule and the charge the atom itself carries. Dipole moment belongs to the geometric descriptor[45, 46], a physical quantity that describes the situation of charge distribution in a molecule. It usually contains information about the property and location of all atoms and bonds in the molecule, representing properties such as geometry, type of chemical bonds and so on of the molecule.
Molecular weight is the sum of the relative atomic mass of all atoms in a molecule. EHOMO represents the molecular orbital with the highest energy occupied by electrons. With the increase of atomic number, the effective nuclear charge and the number of the main quantum also increases, leading to the electron moving towards the orbital of higher energy level, so that the molecular orbital energy is affected by the type of atoms, the number and the spatial distance of the atoms[47].
3.6 Model comparison between QSAR and CA
The QSAR model is used to quantitatively analyze the toxicity of mixtures based on the molecular structure information of mixtures, while the CA model is used to qualitatively analyze the toxicity of mixtures based on the toxicity of single compounds[48]. Therefore, their toxicity prediction ability on binary mixtures also has a large gap. Moreover, it could be seen from Fig. 4 that the QSAR model has a higher fitting degree than the CA model. The RMSE of QSAR model at EC50, EC30 and EC10 were 0.1033, 0.1196 and 0.1759, respectively, while 0.4273, 0.4182 and 0.4818 for the CA model. It could be concluded that the experimental value of the CA model has a great deviation from the predicted one, and the QSAR model has higher toxicity predictive ability than the CA model at all three concentration effects. In addition, models pEC50 and pEC30 had higher R2 (0.9403 and 0.9298) and lower RMSPext (0.142 and 0.144), and their predictive ability and robustness were significantly better than those of model pEC10 (R2 = 0.8564 and RMSPext = 0.1781). By combining section 3.1 analysis, 16, 15 and 10 binary mixture rays with synergistic effect could be seen in models pEC50, pEC30 and pEC10, respectively, which shows that with the increase of the synergistic effect of the mixture, the predictive ability of established QSAR model is more excellent. Thus, the QSAR model can predict the synergistic toxicity value of binary mixtures more accurately.
Figure 4
4. CONCLUSION
The concentration-response curves of S. obliquus for five pesticides and their 35 binary mixture rays could all be well fitted by Logistic or Weibull functions. The toxicity order of five pesticides was metribuzin > linuron > dichlorvos > trichlorfon > dimethoate. The freshwater green algae S. obliquus was more sensitive to two herbicides (linuron and metribuzin) than the insecticide. The toxicity of a single pesticide may be related to its cyclic structure. Metribuzin and linuron with cyclic structure had higher toxicity than other pesticides.
The mixtures of linuron and trichlorfon, dichlorvos and metribuzin, dimethoate and metribuzin exhibited synergistic effects, while the remaining binary mixtures exhibited additive effects. Selecting CA as an additive reference model to evaluate the toxicity interaction of binary mixtures of pesticides could found that 46%, 43% and 29% of the binary mixtures have synergistic effects at EC50, EC30 and EC10 concentrations, respectively, indicating that the interaction model of chemicals may change with the variation of mixture concentration levels or concentration ratios, and the higher the concentration level, the greater the possibility of synergistic effect.
Mixed structure descriptors can effectively characterize the overall molecular structure of the mixture. The QSAR models established at the effect concentrations of EC50, EC30 and EC10 had good internal robustness (both R2 and Q2 > 0.8) and external predictive ability (QF2 > 0.8, CCC > 0.85). The excellent degree of the model was model pEC50 > model pEC30 > model pEC10, and the predictive ability was better than that of the CA model under the same concentration effect. Therefore, three models may be useful in predicting unknown toxicity values of the binary pesticide mixtures. In addition, compared to additive, three models can more accurately predict the toxicity of binary mixtures of pesticides with a synergistic effect.
-
-
[1]
Papa, E.; Battaini, F.; Gramatica, P. Ranking of aquatic toxicity of esters modelled by QSAR. Chemosphere 2005, 58, 559−570. doi: 10.1016/j.chemosphere.2004.08.003
-
[2]
Park, J. A.; Abd El-Aty, A. M.; Zheng, W.; Kim, S. K.; Cho, S. H.; Choi, J. M.; Hacimuftuo, A.; Jeong, J. H.; Wang, J.; Shim, J. H.; Shin, H. C. Simultaneous determination of clanobutin, dich-lorvos, and naftazone in pork, beef, chicken, milk, and egg using liquid chromatography-tandem mass spectrometry. Food Chem. 2018, 252, 40−48. doi: 10.1016/j.foodchem.2018.01.085
-
[3]
Yu, Y.; Hu, S.; Yang, Y.; Zhao, X.; Xue, J.; Zhang, J.; Gao, S.; Yang A. Successive monitoring surveys of selected banned and restricted pesticide residues in vegetables from the northwest region of China from 2011 to 2013. Bmc. Pub. Hea. 2018, 18, 91−100. doi: 10.1186/s12889-017-4632-x
-
[4]
Zheng, S.; Chen, B.; Qiu, X.; Chen, M.; Ma, Z.; Yu, X. Distribution and risk assessment of 82 pesticides in jiulong river and estuary in south China. Chemosphere 2016, 144, 1177−1192. doi: 10.1016/j.chemosphere.2015.09.050
-
[5]
Ccanccapa, A.; Masiá, A.; Andreu, V. Spatio-temporal patterns of pesticide residues in the turia and júcar rivers (Spain). Sci. Total Environ. 2016, 540, 200−210. doi: 10.1016/j.scitotenv.2015.06.063
-
[6]
Xu, Y. C.; Wang, S. S.; Xu, J. J.; Yu, G. M. Monitoring pesticide residues in source of drinking water in rural area, Yantai. Mod. Prev. Med. 2015, 42, 1704−1707.
-
[7]
Chen, C.; Zou, W. B.; Cui, G. L.; Tian, J. C.; Wang, Y. C.; Ma, L. M. Ecological risk assessment of current-use pesticides in an aquatic system of Shanghai, China. Chemosphere 2020, 257, 127−222.
-
[8]
Tien, C. J.; Chen, C. S. Assessing the toxicity of organophosphorous pesticides to indigenous algae with implication for their ecotoxicological impact to aquatic ecosystems. J. Envir. Sci. Hea. Part. B 2012, 47, 901−912. doi: 10.1080/03601234.2012.693870
-
[9]
Wan, L.; Wu, Y.; Ding, H.; Zhang, W. Toxicity, biodegradation, and metabolic fate of organophosphorus pesticide trichlorfon on the freshwater algae chlamydomonas reinhardtii. J. Agric. Food Chem. 2020, 68, 1645−1653. doi: 10.1021/acs.jafc.9b05765
-
[10]
Liu, S. S.; Wang, C. L.; Zhang, J.; Zhu, X. W.; Li, W. Y. Combined toxicity of pesticide mixtures on green algae and photobacteria. Ecotoxicol. Environ. Saf. 2013, 95, 98−103. doi: 10.1016/j.ecoenv.2013.05.018
-
[11]
Tao, Y.; Jia, C.; Jing, J.; Zhang, J.; Yu, P.; He, M.; Wu, J.; Chen, L.; Zhao, E. Occurrence and dietary risk assessment of 37 pesticides in wheat fields in the suburbs of Beijing, China. Food Chem. 2021, 350, 129245. doi: 10.1016/j.foodchem.2021.129245
-
[12]
Du, L.; Li, S.; Qi, L.; Hou, Y.; Yan, Z.; Wei, X.; Wang, H.; Zhao, X.; Sun, C. Metabonomic analysis of the joint toxic action of long-term low-level exposure to a mixture of four organophosphate pesticides in rat plasma. Mol. Biosyst. 2014, 10, 1153−1161. doi: 10.1039/C4MB00044G
-
[13]
Qin, L. T.; Chen, Y. H.; Zhang, X.; Mo, L. Y.; Zeng, H. H.; Liang, Y. P. QSAR prediction of additive and non-additive mixture toxicities of antibiotics and pesticide. Chemosphere 2018, 198, 122−129. doi: 10.1016/j.chemosphere.2018.01.142
-
[14]
Mo, L. Y.; Zhao, D. N.; Qin, M.; Qin, L. T.; Zeng, H. H.; Liang, Y. P. Joint toxicity of six common heavy metals to chlorella pyrenoidosa. Environ. Sci. Pollut. Res. 2017, 26, 30554−30560.
-
[15]
Mo, L. Y.; Liu, J.; Qin, L. T.; Zeng, H. H.; Liang, Y. P. Two-stage prediction on effects of mixtures containing phenolic compounds and heavy metals on Vibrio qinghaiensis sp. Q67. Bull. Environ. Contam. Toxicol. 2017, 99, 17−22. doi: 10.1007/s00128-017-2099-1
-
[16]
Zhang, S. N.; Su, L. M.; Zhang, X. J.; Li, C.; Qin, W. C.; Zhang, D. M.; Liang, X. X.; Zhao, Y. H. Combined toxicity of nitro-substituted benzenes and zinc to photobacterium phosphoreum: evaluation and QSAR analysis. Int. J. Env. Res. Pub. He. 2019, 16, 1041−1052. doi: 10.3390/ijerph16061041
-
[17]
Dou, R. N.; Liu, S. S.; Mo, L. Y.; Liu, H. L.; Deng, F. C. A novel direct equipartition ray design (EquRay) procedure for toxicity interaction between ionic liquid and dichlorvos. Environ. Sci. Pollut. Res. 2011, 18, 734−742. doi: 10.1007/s11356-010-0419-7
-
[18]
Zhou, B.; Xin, L. The monitoring of chemical pesticides pollution on ecological environment by GIS. Environ. Technol. Inno. 2021, 34, 101506.
-
[19]
Calvo, S.; Romo, S.; Soria, J. Pesticide contamination in water and sediment of the aquatic systems of the natural park of the albufera of valencia (spain) during the rice cultivation period. Sci. Total Environ. 2021, 774, 145009. doi: 10.1016/j.scitotenv.2021.145009
-
[20]
Thomas, M. C.; Flores, F.; Kaserzon, S. Toxicity of ten herbicides to the tropical marine microalgae Rhodomonas salina. Sci. Rep. 2020, 10, 7612. doi: 10.1038/s41598-020-64116-y
-
[21]
Ge, H. L.; Liu, S. S.; Su, B. X. Predicting joint toxicity of organophosphorus and triazine pesticides on green algae using the generalized concentration addition model. J. Environ. Sci. 2014, 34, 2413−2419.
-
[22]
Owczarek, K.; Kudak, B. J.; Simeonov, V.; Mazerska, Z.; Namienik, J. Binary mixtures of selected bisphenols in the environment: their toxicity in relationship to individual constituents. Molecules 2018, 23, 3226−3239. doi: 10.3390/molecules23123226
-
[23]
Liu, S. S.; Zhang, J.; Zhang, Y. H.; Qin, L. T. APTox: assessment and prediction on toxicity of chemical mixtures. Acta Chim. Sin. 2012, 70, 1511−1517. doi: 10.6023/A12050175
-
[24]
Qu, R. J.; Liu, H. X.; Feng, M. B.; Yang, X.; Wang, Z. Y. Investigation on intramolecular hydrogen bond and some thermodynamic properties of polyhydroxylated anthraquinones. J. Chem. Eng. Data 2012, 57, 2442−2455. doi: 10.1021/je300407g
-
[25]
Shi, J. Q.; Qu, R. J.; Feng, M. B.; Wang, X. G.; Wang, L. S.; Yang, S. G.; Wang, Z. Y. Oxidative degradation of decabromodiphenyl ether (BDE 209) by potassium permanganate: reaction pathways, kinetics, and mechanisms assisted by density functional theory calculations. Environ. Sci. Technol. 2015, 49, 4209−4217. doi: 10.1021/es505111r
-
[26]
Andrea, M.; Viviana, C.; Manuela, P.; Roberto, T. Dragon software: an easy approach to molecular descriptor calculations. Match-Commun. Math. Co. 2006, 56, 237−248.
-
[27]
Chatterjee, M.; Roy, K. Prediction of aquatic toxicity of chemical mixtures by the QSAR approach using 2D structural descriptors. J. Hazard. Mater. 2021, 408, 124936. doi: 10.1016/j.jhazmat.2020.124936
-
[28]
Kurt, B. Z.; Gazioglu, I.; Sonmez, F.; Kucukislamoglu, M. Synthesis, antioxidant and anticholinesterase activities of novel coumarylthiazole derivatives. Bioorg. Chem. 2015, 59, 80−90. doi: 10.1016/j.bioorg.2015.02.002
-
[29]
Gramatica, P.; Chirico, N.; Papa, E.; Cassani, S.; Kovarich, S. QSARINS: a new software for the development, analysis, and validation of QSAR MLR models. J. Comput. Chem. 2013, 34, 2121−2132. doi: 10.1002/jcc.23361
-
[30]
Kunal, R.; Supratik, K.; Pravin, A. On a simple approach for determining applicability domain of QSAR models. Chemometr. Intell. Lab. Syst. 2015, 145, 22−29. doi: 10.1016/j.chemolab.2015.04.013
-
[31]
Jonker, M. J.; Svendsen, C.; Bedaux, J. J. M.; Bongers, M.; Kammenga, J. E. Significance testing of synergistic/antagonistic, dose level-dependent, or dose ratio-dependent effects in mixture dose-response analysis. Environ. Toxicol. Chem. 2005, 24, 2701−2713. doi: 10.1897/04-431R.1
-
[32]
Syberg, K.; Elleby, A.; Pedersen, H.; Cedergreen, N.; Forbes, V. E. Mixture toxicity of three toxicants with similar and dissimilar modes of action to Daphnia magna. Ecotoxicol. Environ. Saf. 2008, 69, 428−436. doi: 10.1016/j.ecoenv.2007.05.010
-
[33]
Eriksson, L.; Jaworska, J.; Worth, A. P.; Cronin, M.; Mcdowell, R. M. Methods for reliability and uncertainty assessment and for applicability evaluations of classification- and regression-based QSARs. Environ. Health Persp. 2003, 111, 1361−1375. doi: 10.1289/ehp.5758
-
[34]
Tropsha, A. Best practices for QSAR model development, validation, and exploitation. Mol. Inform. 2010, 29, 476−488. doi: 10.1002/minf.201000061
-
[35]
Chirico, N.; Gramatica, P. Real external predictivity of QSAR models: how to evaluate it? Comparison of different validation criteria and proposal of using the concordance correlation coefficient. J. Chem. Inf. Model. 2011, 51, 2320−2335. doi: 10.1021/ci200211n
-
[36]
Kiralj, R.; Ferreira, M. Basic validation procedures for regression models in QSAR and QSPR studies: theory and application. J. Brazil. Chem. Soc. 2008, 20, 770−787.
-
[37]
Shi, L. M.; Fang, H.; Tong, W. QSAR models using a large diverse set of estrogens. J. Chem. Inf. Comp. Sci. 2001, 41, 186−195. doi: 10.1021/ci000066d
-
[38]
Tropsha, A.; Gramatica, P.; Gombar, V. The importance of being earnest: validation is the absolute essential for successful application and interpretation of QSPR models. QSAR Comb. Sci. 2003, 22, 69−77. doi: 10.1002/qsar.200390007
-
[39]
Ghodsi, R.; Hemmateenejad, B. QSAR study of diarylalkylimidazole and diarylalkyltriazole aromatase inhibitors. Med. Chem. Res. 2016, 25, 834−842. doi: 10.1007/s00044-016-1530-1
-
[40]
Asadollahi, T.; Dadfarnia, S.; Shabani, A. M. H.; Ghasemi, J. B.; Sarkhosh, M. QSAR models for cxcr2 receptor antagonists based on the genetic algorithm for data preprocessing prior to application of the PLS linear regression method and design of the new compounds using in silico virtual screening. Molecules 2011, 16, 1928−1955. doi: 10.3390/molecules16031928
-
[41]
Yang, F.; Wang, M.; Wang, Z. Y. Sorption behavior of 17 phthalic acid esters on three soils: effects of pH and dissolved organic matter, sorption coefficient measurement and QSPR study. Chemosphere 2013, 93, 82−89. doi: 10.1016/j.chemosphere.2013.04.081
-
[42]
Zhang, Q. Y.; Hu, W. P.; Hao, J. F.; Liu, X. H.; Xu, L. Chiral topological charge index and its applications. Acta Chim. Sin. 2010, 68, 883−888.
-
[43]
Wang, X.; Jie, O.; Zhao, F. Local kronecker delta property of the MLS approximation and feasibility of directly imposing the essential boundary conditions for the EFG method. Eng. Anal. Bound. Elem. 2013, 37, 1021−1042. doi: 10.1016/j.enganabound.2013.03.011
-
[44]
Han, J.; Dai, C.; Yu, G.; Lei, Z. Parameterization of COSMO-RS model for ionic liquids. Green Energy Environ. 2018, 3, 247−265. doi: 10.1016/j.gee.2018.01.001
-
[45]
Cao, J. S.; Wei, M. J.; Chen, F. W. Relationship between the bond dipole moment and bond angle of polar molecules. Acta Phys. Chim. Sin. 2016, 32, 1639−1648. doi: 10.3866/PKU.WHXB201604062
-
[46]
Fu, X. M.; Li, Y.; Wang, J. H. A study of the influential factors on the dipole moments of small organic. Comput. Appl. Chem. 2015, 32, 408−412.
-
[47]
Zeng, X. L.; Qu, R. J.; Feng, M. B.; Chen, J.; Wang, L. S.; Wang, Z. Y. Photodegradation of polyfluorinated dibenzo-p-dioxins (PFDDs) in organic solvents: experimental and theoretical studies. Environ. Sci. Technol. 2016, 50, 8128−8134. doi: 10.1021/acs.est.6b02682
-
[48]
Liu, H. X.; Shi, J. Q.; Liu, H.; Wang, Z. Y. Improved 3D-QSPR analysis of the predictive octanoleair partition coefficients of hydroxylated and methoxylated polybrominated diphenyl ethers. Atmos. Environ. 2013, 77, 840−845. doi: 10.1016/j.atmosenv.2013.05.068
-
[1]
-
Table 1. Fitted CRC Parameters (α and β), Fitted Statistics (R2 and RMSE), and EC(10, 30, 50) of Five Pesticides
Pesticide CAS RN F α β RMSE R2 EC50 EC30 EC10 Linuron 330-55-2 L 27.33 3.90 0.0607 0.9899 9.824E-08 5.957E-08 2.685E-08 Dimethoate 60-51-5 W 6.39 2.28 0.0605 0.9808 9.304E-04 5.562E-04 1.623E-04 Dichlorvos 62-73-7 W 6.26 2.16 0.0528 0.9704 7.252E-04 4.213E-04 1.148E-04 Trichlorfon 52-68-6 L 14.48 4.66 0.0783 0.9713 7.811E-04 5.139E-04 2.638E-04 Metribuzin 21087-64-9 L 29.87 4.17 0.0524 0.9809 6.870E-08 4.303E-08 2.042E-08 F: fitted functions where L refers to Logit function and W to Weibull function; α and β are fitting function parameters;
CAS RN is the chemical abstracts service register number; R2 and RMSE are the fitting function statistic. -
 扫一扫看文章
扫一扫看文章
计量
- PDF下载量: 19
- 文章访问数: 1568
- HTML全文浏览量: 97

 DownLoad:
DownLoad:




 下载:
下载:

