English

• 自2004年英国曼彻斯特大学的Geim和Novoselov采用机械剥离的方法首次成功地将石墨层片剥离，得到单层石墨烯以来^[1]，石墨烯便以优异的电学、热学、光学和力学性能，高的理论比表面积，以及完美的量子隧道效应和整数的量子霍尔效应引起了全世界科学家广泛的关注。石墨烯是唯一稳定存在的二维单原子层厚度碳材料^[2]，厚度为0.35nm左右。理想的石墨烯结构是由碳六角形蜂巢结构组成的二维周期蜂窝状结构^[3]，每个碳原子均为sp²杂化，并贡献p轨道上的一个剩余电子形成大π键。

  石墨烯按层数分类，可以分为单层石墨烯、双层石墨烯、少层石墨烯、多层石墨烯。单层石墨烯是指由一层六角形蜂巢结构周期性紧密堆积的碳原子构成的二维碳材料；双层石墨烯则是由两层六角形蜂巢结构周期性紧密堆积的碳原子构成；少层石墨烯是由3~10层六角形蜂巢结构周期性紧密堆积的碳原子层以不同方式堆垛(包括ABC堆垛、ABA堆垛等)而成；多层石墨烯是指厚度在10层以上、六角形蜂巢结构周期性紧密堆积的碳原子以不同方式堆垛(包括ABC堆垛、ABA堆垛等)构成的二维碳材料。除此之外，研究人员还以化学还原和热还原的方法制备出一种石墨烯纸。

  石墨烯具有众多优异的性能，包括超高的载流子迁移率(10⁵cm²·V^-1·s^-1)^[5]，是Si的100倍；石墨烯的弹性模量高达1TPa，抗压强度达到了180GPa，是钢材的100倍^[6]。除此之外，在热学性能方面，石墨烯也被认为是迄今为止最好的传热材料，它的热导率可以高达5000W/mK^[4]，大约是金刚石的5倍，是铜的10倍。本文将围绕石墨烯的热学性能对最近国内外该领域的研究成果进行综述。

  1   石墨烯的导热机理

  一般采用热导率来描述一种材料的导热性能。热导率是指在物体内部垂直于导热方向取两个相距1m、面积为1m²的平行平面，若两个平面的温度相差1K，则在1秒内从一个平面传导至另一个平面的热量就规定为该物质的热导率，其单位为W/mK。

  石墨烯是一种层状结构材料，其热学性质主要是由晶格振动引起的，有文献报道通过计算石墨烯内光学声子与声学声子的色散曲线，发现在石墨烯内有六种极性声子，分别为：(1) 平面外的声学声子(ZA模声子)和光学声子(ZO模声子)；(2) 平面内横向声学声子(TA模声子)和横向光学声子(TO模声子)；(3) 平面内的纵向声学声子(LA模声子)和纵向光学声子(LO模声子)^[7]。

  研究人员通过研究声子的弛豫时间以及弛豫时间随波矢、频率和温度的变化关系发现，声学声子对热导率的贡献可高达95%^[6]。石墨烯中参与热传导的主要是3类声学声子，即LA模声子、TA模声子、ZA模声子，其中前两类是面内传输模式，有着线性的散射关系，后一类是面外传输模式，存在非线性的二次散射关系^[8]。Lindsay等^{[7, 9]}认为，ZA模声子对传热的贡献大于LA模声子和TA模声子之和，可占到75%。

  基于以上理论研究，石墨烯被预测存在超高的热导率。目前，常用的导热材料中，铝箔的热导率为160W/mK，铜的热导率为380W/mK，单壁碳纳米管(SWCNTs)的热导率为3500W/mK^[10]，多壁碳纳米管(MWCNTs)的热导率为3000W/mK^[11]，金刚石的热导率在1000~2200 W/mK之间^[12]。研究结果表明，单层石墨烯拥有高达5000W/mK的热导率。不同形态石墨烯材料的热导率见表 1。

  表 1  石墨烯材料的热导率 Table 1.  Thermal conductivity of graphene materials

  表选项

  导出Excel

  下载全尺寸表图像

  样品	热导率/(W/mK)	方法	参考文献
  单层机械剥离石墨烯(悬浮)	4840~5300	拉曼光热法	[23]
  单层CVD石墨烯(悬浮)	(2500+1100/-1050)(室温) (1400+500/-480)(500K)	拉曼光热法	[28]
  单层石墨烯(支撑)	600	热电桥法	[17]
  二氧化硅包裹单层石墨烯	160	热分布的方法	[32]
  少层石墨烯(2~4层)	1300~2800	拉曼光热法	[37]
  多层还原氧化石墨烯	1043.5	激光闪射法	[43]
  石墨	2000	理论：模型计算	[38]
  石墨烯纳米带(1nm厚、光滑边缘)	3000	理论：动力学模型	[15]
  石墨烯纳米带(1nm厚、粗糙边缘)	500	理论：动力学模型	[15]

  从表 1可以发现，不同状态下石墨烯的热导率有很大差别，接下来重点介绍石墨烯热导率的主要影响因素。

  2   石墨烯热导率的影响因素

  声子的传输模式和散射机制对石墨烯的热导率有重要影响，热导率主要由石墨烯声子频率、声子自由程、声子作用过程等因素决定。研究发现影响热导率的因素有缺陷、基底及边缘等。

  2.1   缺陷

  运用分子动力学研究发现，缺陷密度对热导率有显著影响，尤其当缺陷态浓度较低时此影响更加明显，导致这一现象的原因是声子平均自由程的减小^[13]。在石墨烯中存在单原子缺失和Stone-Wales位错两种缺陷，研究者分别研究了单原子缺陷浓度与Stone-Wales缺陷浓度对石墨烯热导率的影响。结果表明，单原子缺陷浓度达到0.175%时，石墨烯的热导率降低到原来的一半；当Stone-Wales位错浓度到达0.3%时，石墨烯的热导率也同样降低到原来的一半。

  2.2   基底

  当二维材料与基底接触时，热导率会明显减小，导致这一结果的原因是热传导主要是靠声子传导，当石墨烯与基底接触时表面或边缘扰动会变得非常敏感。有研究指出，处于悬浮状态的单层石墨烯的热导率为5000W/mK，当单层石墨烯与SiO₂基底接触时，其热导率则降至600W/mK，当其被SiO₂包裹时，热导率仅为160W/mK^[14]。

  2.3   边缘

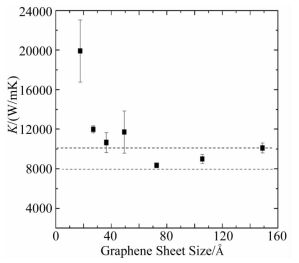
  2010年William等^[15]采用平衡分子动力学模型计算了平滑边缘和粗糙边缘石墨烯纳米带的热导率(如图 1所示)，对于宽度相同的石墨烯纳米带，平滑边缘纳米带的热导率大于粗糙边缘纳米带的热导率。同时他们发现，粗糙边缘纳米带的热导率与纳米带尺寸紧密相关，当石墨烯纳米带宽度小于5nm时拥有很高的热导率，当尺寸大于5nm时，石墨烯纳米带热导率则分布在8000~10000 W/mK之间(如图 2所示)。

  图 1  具有粗燥边缘(左)和平滑边缘(右)的石墨烯纳米带的原子结构^[15] Figure 1.  Atomic structure of rough-edged (left) and smooth-edged (right) GNR models^[15]

  图选项

  下载全尺寸图像

  下载幻灯片

  图 2  石墨烯纳米带宽度与热导率的关系图^[15] Figure 2.  The relationship between thermal conductivity and size for graphene sheets^[15]

  图选项

  下载全尺寸图像

  下载幻灯片

  3   石墨烯热导率的模型计算

  目前研究石墨烯热传导的理论计算主要是通过研究石墨烯蜂巢晶格原子改变来揭示热流改变和调整的分子动力学模型^[14]，以及基于量子运输研究而发展起来的具有一套完备数理方法的非平衡态格林函数^[16]。

  3.1   分子动力学模型

  材料的热导率一般与声子的弛豫时间密切相关^[17]。Qiu等^[18]运用分子动力学模型与声子光谱分析相结合，在室温下分析提取了单层(支撑、悬浮)石墨烯的声子弛豫时间，发现当石墨烯放在基底上时，所有分支的声子弛豫时间都会减小，原因是基底散射和面内与面外的声子散射对称性被打破，从而使热导率降低。

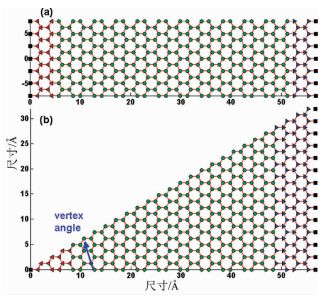
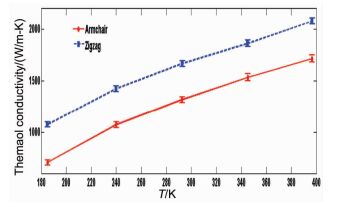
  Hu等^[19]利用分子动力学研究了对称石墨烯纳米带与不对称石墨烯纳米带的热导率(如图 3所示)。他们发现相同尺寸的对称石墨烯纳米带的热导率大于不对称石墨烯纳米带的热导率，原因是在不对称石墨烯纳米带中存在热整流。他们比较了边缘手性对热导率的影响，发现具有锯齿型边缘结构纳米带的热导率明显大于具有扶手椅型边缘结构的纳米带，原因是扶手椅型边缘是不规则的，导致强烈的声子散射(如图 4所示)。

  图 3  对称石墨烯纳米带(a)与不对称石墨烯纳米带(b)的结构^[19] Figure 3.  Structure of symmetric(rectangle) (a) and asymmetric (triangle) (b) graphene nanoribbons^[19]

  图选项

  下载全尺寸图像

  下载幻灯片

  图 4  扶手椅型和Z型石墨烯纳米带的热导率^[19] Figure 4.  Thermal conductivity of armchair and zigzag GNRs^[19]

  图选项

  下载全尺寸图像

  下载幻灯片

  Zhang等^[20]利用平衡态分子动力学研究了300K下不同同位素浓度的石墨烯的热导率，发现改变同位素浓度时热导率会发生变化，当同位素浓度为25%时，锯齿型和扶手椅型石墨烯热导率均会减小80%。

  3.2   格林函数

  Wu等^[21]利用非平衡态格林函数研究存在空位缺陷的石墨烯纳米带和存在Si缺陷石墨烯纳米带的热导率，结果表明，热导率对空位缺陷非常敏感，对Si缺陷不敏感。研究中还发现，边缘空位缺陷对石墨烯纳米带热导率的影响非常的小，原因是边缘空位缺陷仅仅是引起了边缘重组，而内部空位缺陷会使声子散射增强，大大减小石墨烯纳米带的热导率。

  Nuo等^[22]通过分子动力学和非平衡态格林函数来研究折叠石墨烯纳米带的热导率。他们发现折叠会降低石墨烯纳米带的热导率，并且折叠次数越多，石墨烯纳米带的热导率减小的比例越大。

  利用模型计算只能研究理想本征石墨烯的热导率，对于实际石墨烯的热导率仍需利用实验的方法来对其进行测试。

  4   石墨烯热导率的测试方法

  人们进行了大量关于石墨烯热导率测试的研究。以下按照石墨烯材料层数的不同，对其热导率测试方法进行分别介绍。

  4.1   单层石墨烯热导率的测试

  4.1.1   单层悬浮石墨烯热导率的测试

  近年来，研究者对石墨烯的热学性能日益关注，对石墨烯热导率的实验测试研究越来越多^{[4, 23, 27~28]}。Balandin等^[23]首次报道用拉曼法来测量单层悬浮石墨烯热导率，他们测得的机械剥离法制备的石墨烯的热导率为3000~5000W/mK。Cai等^[28]测量了悬浮状态下化学气相沉积(CVD)法制备的石墨烯的热导率，常温下单层悬浮石墨烯的热导率为(2500+1100/-1050) W/mK，在500K时为(1400+500/-480) W/mK。以上两个测试过程中均忽略了周围环境热扩散的影响。Chen等^[27]测试了真空、CO₂气氛以及空气氛围下CVD生长的单层悬浮石墨烯的热导率，该实验考虑了周围环境的热损失，测试结果发现空气中测得的值比真空中高14%~40%。

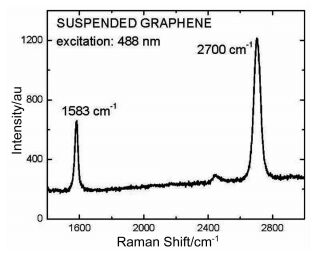
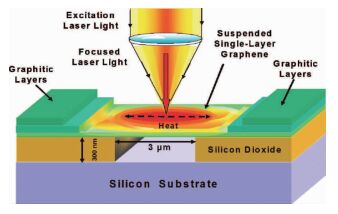
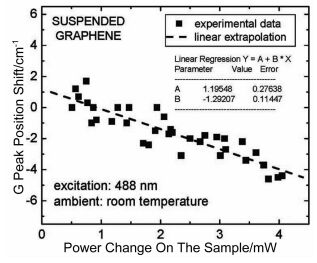
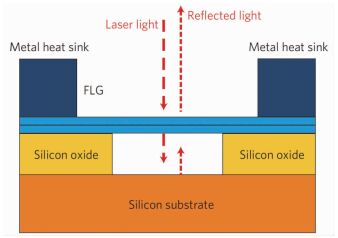
  拉曼测试石墨烯热导率是根据石墨烯在拉曼光谱中有非常清晰的峰(如图 5所示)^[24]以及石墨烯的峰位置对温度有很强的依赖性^[25]等特性来进行测量的。应用拉曼法测量石墨烯热导率时是将样品悬浮放置于样品架或者样品台上(如图 6所示)，随后由激光器产生的激光对样品进行加热，然后测试拉曼峰位随入射功率的变化关系，以及拉曼峰位与温度的关系。Balandin等^[23]首先采用机械剥离法制备了单层石墨烯，并将石墨烯转移到沟槽之上，在距离沟槽9~10 μm处附加上大块石墨片作为散热器。实验过程中用激光照射样品的中间位置，用共聚焦拉曼光谱仪测量出G峰位置与总功率P_D变化的关系(如图 7所示)。当温度升高时，石墨烯G峰会发生红移，再测量出温度系数χ_G。这一过程中需要测试不同温度下的石墨烯G峰的位置，也就是G峰位置随温度变化曲线的斜率^{[25, 27~28]}，因为P_D=P+P_Si(P_D代表激光的总消耗功率、P代表石墨烯表面的功率消耗、P_Si代表Si基底的功率消耗)，需要经过多次测量找出P与P_D之间的关系。然后利用理论公式(1)，计算出单层悬浮石墨烯的热导率。

  图 5  单层悬挂石墨烯拉曼光谱的G峰及2D特征峰^[23] Figure 5.  Raman spectrum of suspended graphene showing the G peak and 2D band features characteristic for single-layer graphene^[23]

  图选项

  下载全尺寸图像

  下载幻灯片

  图 6  显示激光聚焦于悬挂在沟槽上的石墨烯层上的实验示意图^[23] Figure 6.  Schematic of the experiment showing the excitation laser light focused on a graphene layer suspended across a trench^[23]

  图选项

  下载全尺寸图像

  下载幻灯片

  图 7  总消耗功率与石墨烯G峰位置的关系图^[23] Figure 7.  Shift in graphene G peak spectral position vs change in total dissipated power^[23]

  图选项

  下载全尺寸图像

  下载幻灯片

  其中，χ_G为温度系数；δω为拉曼光谱G峰的偏移量；δP为石墨烯吸收的激光功率的变化值；(δω/δP)表示G峰峰值随石墨烯表面消耗功率的变化情况；L为石墨烯片中心点至热沉边缘的距离；W为石墨烯片的宽度；h为石墨烯的厚度(h=0.35±0.01nm)。

  4.1.2   单层支撑石墨烯热导率的测试

  利用热电桥装置来测试碳纳米管的热传导先前已经有过很多报道^[29~30]，使用热电桥装置的原因是RT型电阻温度计测得的温度比用拉曼光谱仪测得的温度精确。为了更准确地测量石墨烯的热导率，Seol等^[17]利用热电桥法测试了单层支撑石墨烯的热导率。Wang等^[31]同样用热桥装置测试了不同尺寸单层支撑石墨烯的热导率。Jang等^[32]利用热分布的方法测量了用SiO₂包裹的石墨烯的热导率，其测定值为160W/mK。

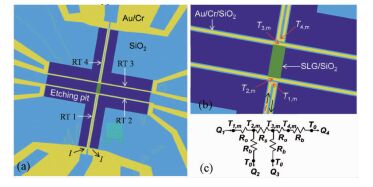
  热电桥法是采用SiO₂或者SiN_x层作为机械支撑系统，一个金属层在上面作为金属电阻计。根据金属电阻计的阻值变化来计算温度的变化量，进而计算出石墨烯的热导率。Seol等^[17]在实验过程中将剥离的单层石墨烯置于SiO₂薄片上放置到Si衬底，然后采用电子束曝光和金属剥离技术，在中间制作出深度为300nm的悬浮SiO₂条带，将石墨烯放置到SiO₂条带上，在悬浮的石墨烯/SiO₂条带两端各放置一条直线型和一条U型的宽1μm、长120μm的由5nm厚Cr和50nm厚Au组成的金属电阻温度计(RTJ，J=1、2、3、4，电阻温度计是根据导体电阻随温度而变化的规律来测量温度的温度计，最常用的电阻温度计都采用金属丝绕制成感温元件)。两条内部的直线与石墨烯片的两端相连，外部的U型线不与石墨烯相连(如图 8所示)，经过以上步骤完成了实验装置的制作。图中浅蓝色部分为SiO₂条带，深蓝色部分为悬浮的SiO₂膜和Si衬底中形成的蚀刻坑，黄色部分为电阻温度计线和接触板。实验过程中对外线(RT1) 进行电加热，然后测量每条RTJ上的温升，通过计算得到单层支撑石墨烯的热导率。

  图 8  测试装置的电子束刻释示意图(a，b)和装置热电路图(c)^[17] Figure 8.  Electron beam lithography layout schematic of the device for thermal measurement (a, b), and evice thermal circuit diagram(c)^[17]

  图选项

  下载全尺寸图像

  下载幻灯片

  对外线(RT1) 进行电加热，那么根据一维热力学方程知道，RT1中的温升符合下面抛物线方程：

  其中，T₀表示基底温度；Q为电加热量；k_b为有效热导率；L、A分别为SiO₂梁上由Au/Cr组成的RT1的长度和横截面积。

  根据边界条件(3)、(4) 计算C₁、C₂：

  则RT1的温度曲线，如式(5) 所示：

  根据能量守恒、热回路(见图 8c)推出：

  R_b为每条RT线与SiO₂横梁的热阻值；R_{b, J}(J=1、2、3、)为RTJ在没有内部加热时T_{J, m}与周围环境的热阻；Q是RT1电加热量；ΔT_{J, m} (J=1、2、3、4) 是RTJ线中心位置的温升。

  因为在其他的3条RT线的中心和结束端存在线性温度曲线，所以最高的温度出现在中心位置。根据线性温度曲线得出^[17]：

  $\overline {\Delta {T_{\rm{J}}}} $ (J=1、2、3、4) 为平均温升(利用四探针法测得电阻与电阻温度系数，计算出温度变化)；ΔT_{J, m}是RTJ线中心位置的温升。

  根据公式(5) 和(7) 得到在RT1中的温升为：

  则，

  根据热力循环，中间横梁的热阻为：

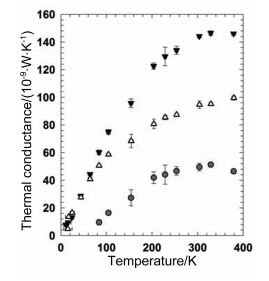
  此时G为单层石墨烯/SiO₂的热导，为了计算单层支撑石墨烯的热导，将其用氧等离子体蚀刻，然后测得SiO₂的热导(如图 9所示)。于是可以求得单层支撑石墨烯热导(G_g)。再根据K=(G_gL)/Wt，(t是石墨烯的厚度，0.35nm)得出热导率值，室温下其测量值约为600W/mK。

  图 9  刻蚀前后热导率与单层支撑石墨烯热导率的比较(实心倒三角表示蚀刻之前热导率，空心正三角表示蚀刻之后热导率，圆圈表示单层支撑石墨烯热导率)^[17] Figure 9.  Measured thermal conductance before (solid downward triangles) and after (unfilled. upward triangles) the SLG was etched, with the difference being the contribution from the SLG(circles)^[17]

  图选项

  下载全尺寸图像

  下载幻灯片

  4.2   少层与多层石墨烯热导率的测试

  已有研究者测得块状石墨的热导率大约为2000W/mK^[33]。借助3D块状石墨的导热研究，也可以更进一步研究2D石墨烯的热导^[34~35]。

  Bao等利用拉曼光热法测试少层石墨烯的热导率，先采用机械剥离的方法从块状石墨上剥离出少层石墨烯，将石墨烯悬挂在带有沟槽的Si/SiO₂圆片上，沟槽深度为300nm、宽为1~5 μm，两边缘放置金属散热片，然后制备高质量的悬浮石墨烯(宽度为5~16 μm)^[36]。实验过程使用不同功率的激光照射少层石墨烯的中间部位(如图 10所示)，用拉曼光谱仪测试少层石墨烯的G峰位置与表面激光功率的关系^[37]。根据有限元法将石墨烯分成不同有限元，设定初始值K₀，通过热扩散方程计算出每个点的温度上升值ΔT_M，与实验测得的温度ΔT_E进行比较，当两者相等时得到的K即为所得热导率。有限差分法还可以算出斜率α=δω/ΔP_D(δω是拉曼的G峰偏移量，ΔP_D为功率变化值)与石墨烯热导率的关系。少层石墨烯的热导率与石墨烯样品的宽度有关^[38~39]，宽度一定时，热导率依赖于声子散射。

  图 10  少层石墨烯的测试装置图^[37] Figure 10.  Low-layer graphene test device^[37]

  图选项

  下载全尺寸图像

  下载幻灯片

  少层石墨烯的声子平均自由程大约是800nm^[40~42]，当石墨烯材料的厚度(H=h×n)小于石墨烯的声子平均自由程时，热导率还可以用公式(13) 估算。

  C_v为比热；υ、τ分别为平均声子速度和寿命。

  4.3   石墨烯纸的热导率的测试

  对于石墨烯纸的热导率大多采用激光闪射法来进行测试^[43]，激光闪射法是用于测试材料导热性能的常用方法，属于导热测试“瞬态法”的一种。根据热导率的定义^[44]可知，热导率与扩散系数、材料的比热容、材料密度之间存在以下关系：

  其中，α为扩散系数；C_P为材料的比热容；ρ为材料的密度。因此，只要测得扩散系数、材料密度、材料比热容就可以按照式(14) 来计算出材料的热导率。

  石墨烯比石墨的热导率高的原因是声子在二维材料及三维材料中的运输方式不同^[45~48]。我们知道缺陷散射和边缘散射会影响热导率^[49]。所以使用激光闪射法测试石墨烯纸的热导率时，在样品制备过程中应注意减少缺陷的产生，为了测试方便，样品一般制备成直径为25.4mm的小圆片。实验一般选用激光闪射仪来测量材料的扩散系数。激光闪射仪的工作原理是由激光源(或闪光氙灯)在瞬间发射一束光脉冲，均匀照射在样品下表面，使其表层吸收光能后温度瞬时升高，并作为热端将能量以一维热传导方式向冷端(上表面)传播^[50~51]。使用红外检测器连续测量上表面中心部位的相应温升过程，得到温度(检测器信号)升高对时间的关系曲线，根据公式(15) 来计算出热扩散系数^[52~53]。

  d为石墨烯层的厚度；t_1/2为半扩散时间。

  比热一般采用差示扫描量热仪来测量，差示扫描量热仪是目前测量比热最有效的一种方法，在测量过程中需要一个与样品界面形状相同、厚度相近、热物性相似、表面结构光滑程度相同且比热值已知的参比标样，与待测样品同时进行表面涂层^[44]。比热是根据蓝宝石法^{[43, 52]}采用公式(16) 测量的：

  DSC_sample、DSC_bas、DSC_standard分别为样品、空白(做基线)样品和标准样品(蓝宝石)的DSC曲线信号的纵坐标热焓对时间的变化率，DSC_sample-DSC_bas表示样品扣除基线后的DSC曲线信号，DSC_standard-DSC_bas表示标准样品扣除基线后的DSC曲线信号；C_p(sample)和C_p(standard)是样品和标准样品的比热；m_sample和m_standard是样品和标准样品的质量。实验时，首先测试空样品的DSC曲线作为基线；然后测试已知C_p的蓝宝石标样的DSC曲线；最后测试样品的DSC曲线。实验结束后，用基线校准蓝宝石标样和样品的DSC曲线，再根据式(16)，采用比较法计算便可得到石墨烯纸的比热。

  密度的计算公式为：

  体积的计算公式为：

  m为样品质量；V为样品的体积；r为样品的半径；d为厚度。膜厚最可能影响热导率，所以一般使用扫描电镜来测量样品的厚度^[43]。测量时至少需要选择10处不同地方进行厚度测试，然后求出10次的平均值。质量测量使用电子精密天平来进行^[52]。

  5   总结

  石墨烯是一种非常优异的二维材料^[54~55]，其本身具有很好的热学性能。近年来，随着石墨烯材料的发展，测试其热导率成为了研究石墨烯材料性能最活跃的领域之一，为石墨烯材料取代其他材料作为电子元件的导热、散热片提供了机会和可能性。本文介绍了石墨烯的导热原理，综述了国内外对石墨烯热导率的理论计算、实验测量等方面的研究进展。虽然目前关于石墨烯热学性能的研究取得了很多成果，但是石墨烯材料热导率的测试方法尚不统一。为了实现石墨烯材料的商业应用，仍需要研究一套标准的石墨烯热导率测试方法。

• 1. [1]

     A K Geim, K S Novoselov. Nature, 2007, 6:183~191.

  2. [2]

     K S Novoselov, A K Geim, S V Morozov et al. Science, 2004, 306(5696):666~669.

  3. [3]

     J S Wu, W Pisula, K Mullen et al. Chem. Rev, 2007, 107(3):718~747.

  4. [4]

     A A Balandin. Nat. Mater., 2011, 10, 569~581.

  5. [5]

     J Xi, M Long, L Tang et al. Nanoseale, 2012, 4(15):4348~4369.

  6. [6]

     C Lee, X Wei, J W Kysar et al. Science, 2008, 321(5887):385~388.

  7. [7]

     L Lindsay, D A Broido, N Mingo. Phys. Rev. B, 2010, 82(11):115427.

  8. [8]

     Y L Xing, K Xu, Y H Liu et al. Chem. Eng., 2015, 236(05).

  9. [9]

     L Lindsay, W Li, N Mingo et al. Phys. Rev. B, 2014, 89(15):155426.

  10. [10]

      P Kim, L Shi, A Majumdar et al. Phys. Rev. Lett., 2001, 87:215502.

  11. [11]

      E Pop, D Mann, Q Wang et al. Nano Lett., 2006, 6(1):96~100.

  12. [12]

      A V Vlasov, A V Khomich, A F Popovich. Diam. Relat. Mater., 2005, 14:589~593.

  13. [13]

      H Feng, D Fang, Z P Xu. Appl. Phys. Lett., 2011, 99:041901.

  14. [14]

      E Pop, V Vsrshney, A K Roy. MRS Bull., 2012, 37:1273~1281.

  15. [15]

      W J Evans, L Hu, P Keblinski. Appl. Phys. Lett., 2010, 96(20):203112.

  16. [16]

      P K Schelling, S R Phillpot, P Keblinski. Phys. Rev. B, 2002, 65:144306.

  17. [17]

      J H Seol, A L Moore, L Lindsay et al. Science, 2010, 328(5975):213~216.

  18. [18]

      B Qiu, X L Ruan. Appl. Phys. Lett., 2012, 100(19):193101.

  19. [19]

      J N Hu, X L Ruan, Y P Chen. Nano Lett., 2009, 9(7):2730~2735.

  20. [20]

      H J Zhang, G Lee, A F Fonseca et al. J. Nanomater., 2010, 537657.

  21. [21]

      J W Jiang, B S Wang, J S Wang. Appl. Phys. Lett., 2011, 98(11):113114.

  22. [22]

      Z Huang, T S Fisher, J T Murthy. J. Appl. Phys., 2010, 108(9):094319.

  23. [23]

      A A Balandin, S Ghosh, W Bao et al. Nano Lett., 2008, 8(3):902~907.

  24. [24]

      A C Ferrari, J C Meyer, V C Scardaci et al. Phys. Rev. Lett., 2006, 97:187401.

  25. [25]

      I Calizo, A A Balandin, W Bao et al. Nano Lett., 2007, 7(9):2645~2649.

  26. [26]

      A Gupta, G Chen, P Joshi et al. Nano Lett., 2006, 6:2667~2673.

  27. [27]

      S S Chen, A L Moore, W W Cai et al. ACS Nano, 2011, 5(1):321~328.

  28. [28]

      W W Cai, A L Moore, Y W Zhu et al. Nano Lett., 2010, 10(5):1645~1651.

  29. [29]

      C H Yu, L Shi, Z Yao et al. Nano Lett., 2005, 5:1842~1846.

  30. [30]

      L Shi, D Y Li, C Yu et al. J. Heat Transfer, 2003, 125:881~888.

  31. [31]

      Z Q Wang, R G Xie, C T Bui et al. Nano Lett., 2011, 11:113~118.

  32. [32]

      W Y Jang, Z Chen, W Z Bao et al. Nano Lett., 2010, 10:3909~3913.

  33. [33]

      P G Klemens. J. Wide Band Gap Mater., 2000, 7:332~339.

  34. [34]

      S Lepri, R Livi, A Politi. Phys. Rep., 2003, 377:1~80.

  35. [35]

      A A Balandin. IEEE Spectrum, 2009, 35~39.

  36. [36]

      W Bao, F Miao, C Chen et al. Nat. Nanotechnol., 2009, 4:562~566.

  37. [37]

      S Ghosh, W Z Bao, D L Nika et al. Nat. Mater., 2010, 9:555~558.

  38. [38]

      D L Nika, S Ghosh, E P Pokatilov et al. Appl. Phys. Lett., 2009, 94:203103.

  39. [39]

      C M Chen, Q Zhang, M G Yang et al. Carbon, 2012, 50:3572~3584.

  40. [40]

      S Ghosh, I Calizo, D Teweldebrhan et al. Appl. Phys. Lett., 2008, 92:151911.

  41. [41]

      E Munoz, J X Lu, B I Yakobson. Nano Lett., 2010, 10:1652~1656.

  42. [42]

      W B Choi, I Lahiri, R Seelaboyina et al. Crit. Rev. Solid State, 2010, 35(1):52~71.

  43. [43]

      N J Song, C M Chen, C L Lu et al. J. Mater. Chem. A, 2014, 2:16563~16568.

  44. [44]

      王东, 孙晓红, 赵维平等.计量与测试技术, 2009, 36(3):38~42.

  45. [45]

      H C Schniepp, J L Li, M J Mcallister et al. J. Phys. Chem. B, 2006, 110(17):8535~8539.

  46. [46]

      S Stankovich, D A Dikin, G H Dommett et al. Nature, 2006, 442:282~286.

  47. [47]

      S Park, K S Lee, G Bozoklu et al. ACS Nano, 2008, 2:572~578.

  48. [48]

      J Haskins, A Kinaci, C Sevik et al. ACS Nano, 2011, 5:3779~3787.

  49. [49]

      M Freitag, M Steiner, Y Martin et al. Nano Lett., 2009, 9(5):1883~1888.

  50. [50]

      K M F Shahil, A A Balandin. Solid State Commun., 2012, 152:1331~1340.

  51. [51]

      Z Y Wei, Z H Ni, K Bi et al. Phys. Lett. A, 2011, 375:1195~1199.

  52. [52]

      Q Q Kong, Z Liu, J G Gao et al. Adv. Funct. Mater., 2014, 24:4222~4228.

  53. [53]

      P Goli, H Ning, X S Li et al. Nano Lett., 2014, 14:1497~1503.

  54. [54]

      徐秀娟, 秦金贵, 李振. 化学进展, 2009, 21:2559~2567.

  55. [55]

      A K Geim. Science, 2009, 324(5934):1530~1534.

• 

  图 1  具有粗燥边缘(左)和平滑边缘(右)的石墨烯纳米带的原子结构^[15]

  Figure 1  Atomic structure of rough-edged (left) and smooth-edged (right) GNR models^[15]

  下载: 全尺寸图片 幻灯片
  

  图 2  石墨烯纳米带宽度与热导率的关系图^[15]

  Figure 2  The relationship between thermal conductivity and size for graphene sheets^[15]

  下载: 全尺寸图片 幻灯片
  

  图 3  对称石墨烯纳米带(a)与不对称石墨烯纳米带(b)的结构^[19]

  Figure 3  Structure of symmetric(rectangle) (a) and asymmetric (triangle) (b) graphene nanoribbons^[19]

  下载: 全尺寸图片 幻灯片
  

  图 4  扶手椅型和Z型石墨烯纳米带的热导率^[19]

  Figure 4  Thermal conductivity of armchair and zigzag GNRs^[19]

  下载: 全尺寸图片 幻灯片
  

  图 5  单层悬挂石墨烯拉曼光谱的G峰及2D特征峰^[23]

  Figure 5  Raman spectrum of suspended graphene showing the G peak and 2D band features characteristic for single-layer graphene^[23]

  下载: 全尺寸图片 幻灯片
  

  图 6  显示激光聚焦于悬挂在沟槽上的石墨烯层上的实验示意图^[23]

  Figure 6  Schematic of the experiment showing the excitation laser light focused on a graphene layer suspended across a trench^[23]

  下载: 全尺寸图片 幻灯片
  

  图 7  总消耗功率与石墨烯G峰位置的关系图^[23]

  Figure 7  Shift in graphene G peak spectral position vs change in total dissipated power^[23]

  下载: 全尺寸图片 幻灯片
  

  图 8  测试装置的电子束刻释示意图(a，b)和装置热电路图(c)^[17]

  Figure 8  Electron beam lithography layout schematic of the device for thermal measurement (a, b), and evice thermal circuit diagram(c)^[17]

  下载: 全尺寸图片 幻灯片
  

  图 9  刻蚀前后热导率与单层支撑石墨烯热导率的比较(实心倒三角表示蚀刻之前热导率，空心正三角表示蚀刻之后热导率，圆圈表示单层支撑石墨烯热导率)^[17]

  Figure 9  Measured thermal conductance before (solid downward triangles) and after (unfilled. upward triangles) the SLG was etched, with the difference being the contribution from the SLG(circles)^[17]

  下载: 全尺寸图片 幻灯片
  

  图 10  少层石墨烯的测试装置图^[37]

  Figure 10  Low-layer graphene test device^[37]

  下载: 全尺寸图片 幻灯片

  表 1  石墨烯材料的热导率

  Table 1.  Thermal conductivity of graphene materials

  样品	热导率/(W/mK)	方法	参考文献
  单层机械剥离石墨烯(悬浮)	4840~5300	拉曼光热法	[23]
  单层CVD石墨烯(悬浮)	(2500+1100/-1050)(室温) (1400+500/-480)(500K)	拉曼光热法	[28]
  单层石墨烯(支撑)	600	热电桥法	[17]
  二氧化硅包裹单层石墨烯	160	热分布的方法	[32]
  少层石墨烯(2~4层)	1300~2800	拉曼光热法	[37]
  多层还原氧化石墨烯	1043.5	激光闪射法	[43]
  石墨	2000	理论：模型计算	[38]
  石墨烯纳米带(1nm厚、光滑边缘)	3000	理论：动力学模型	[15]
  石墨烯纳米带(1nm厚、粗糙边缘)	500	理论：动力学模型	[15]

  下载: 导出CSV
•