
Citation: Yuan Pei, Chen Jian, Pan Deng, Bao Xiaojun. Adsorption and Reaction Kinetic Studies of the Heterogeneous Catalytic Hydrogenation for Polystyrene[J]. Acta Chimica Sinica, 2016, 74(7): 603-611. doi: 10.6023/A16030117

聚苯乙烯非均相催化加氢吸附动力学及反应动力学研究
English
Adsorption and Reaction Kinetic Studies of the Heterogeneous Catalytic Hydrogenation for Polystyrene
-
Key words:
- hydrogenation
- / adsorption
- / kinetics
- / supported catalyst
- / unsaturated polymer
-
1 引言
Kawaguchi等[34, 35]曾提出聚合物在固体表面的吸附理论, 当催化剂孔径(Dp)与聚合物的均方根旋转半径Rg满足以下关系式:
聚合物加氢是改性制备具有特殊性质和结构的弹性体及热塑性材料的过程[1].不饱和聚合物经加氢处理后, 由于不饱和链段的消除, 其抗氧化性能及热稳定性均得到大幅提升, 在特殊环境下其耐溶剂性、耐候性、耐腐蚀性等性能可得到有效改善[2~4].聚苯乙烯(PS)是由苯乙烯加成聚合得到的高分子聚合物, 也是目前应用最为广泛的热塑性塑料, 具有耐水、耐腐蚀、透明度高、易着色、易加工成型等诸多优点[5~12].当聚苯乙烯中苯环上的不饱和键经催化加氢后, 耐热性、抗氧化性和耐紫外安定性等性能都会得到提高[13~17].
聚合物需要改变构型才能进入到催化剂孔道内部, 导致在多孔催化剂中达到饱和吸附所需的时间比在无孔催化剂表面要长得多, 而只有Dp大于5Rg时, 聚合物分子才能自由扩散至催化剂孔道内部. Rybicka等[36]对于共聚物的吸附研究表明, 溶液中的聚合物分子在高温时构型细长、舒展, 在低温时呈球形、线团结构, 说明温度的变化会导致PS分子的构型变化, 从而影响PS的吸附行为, 进而会对PS的加氢反应产生影响.在21世纪前, 对聚合物非均相加氢反应机理的研究停留在定性分析的层面上[29, 31], 迄今为止提出的最为主流的反应机理是“Blocky”加氢机理[29, 37, 38].该机理认为, 不饱和聚合物由于不饱和键与催化剂中的活性中心之间存在一定的相互作用力吸附在催化剂的活性位上, 经部分加氢后, 其与活性位的相对作用力减弱, 并最终从活性位上脱附.欲使聚合物达到更高的加氢度, 则需要再次进行吸附加氢, 但第二次吸附加氢比第一次吸附加氢要困难得多.该机理很好地解释了聚丁二烯及聚异戊二烯等烯烃聚合物的非均相加氢过程[39~41], 但对于聚苯乙烯的非均相加氢过程及其加氢动力学研究鲜有报道.
在前期工作中, 我们成功合成了表面具有贯穿大孔的二氧化硅空心微球为载体制备的负载型钯催化剂(Pd/SHMs), 并用于聚苯乙烯(PS)加氢的性能测试, 结果显示此催化剂对PS有很好的加氢效果[42].在此基础上, 本文进一步对PS在催化剂上的吸附行为及催化加氢反应过程进行了系统研究, 通过实验推导和模拟, 建立了PS吸附动力学模型并确定了PS非均相加氢的反应级数和活化能, 证明了PS的非均相加氢反应符合“Blocky”加氢机理, 为PS催化加氢反应过程的深入研究提供理论基础.
PS催化加氢的研究始于1929年, 加氢过程主要采用均相溶液加氢及非均相溶液加氢法[13~18].由于均相溶液催化剂反应条件温和且催化活性高, 在20世纪60年代已受到广泛关注[13, 19], 有关的动力学研究也较为充分[20~22].而非均相加氢体系比均相加氢体系复杂得多[1, 23~28], 为气-液-固三相反应, 涉及诸多传质过程[18, 29], 且由于PS分子的高黏度、低扩散系数等固有特点[27~32], 使PS分子从溶液扩散至催化剂表面、吸附在活性位上往往需要较长的时间才能完成[29~33], 因此研究PS分子在催化剂表面的吸附行为及加氢过程尤为重要.
2 结果与讨论
2.1 PS吸附动力学
2.2 PS加氢动力学
2.3 PS的部分加氢产物分析及吸附加氢过程研究
采用正己烷萃取分离法, 对总加氢转化率分别为38%、57%以及69%的PS加氢产物进行萃取分离, 均得到了两种不同溶解性质的加氢产物, 测定其加氢转化率列于表 3中.由表 3可以看出, 总加氢转化率不同的三种PS加氢产物, 经过正己烷萃取分离后均可得到两种产物, 其中溶于正己烷萃取相中的聚合物完全烘干除去溶剂后, 分析其加氢度为85%左右, 剩余未溶解的聚合物烘干后测定加氢度低于30%.以上结果与文献报道其他聚合物加氢的“Blocky”机理相似[29].聚合物在吸附加氢过程中, 只有当加氢度达到一定程度后才会发生脱附.如果需要达到更高的加氢度, 聚合物分子需进行二次或多次吸附加氢, 但二次吸附加氢比第一次吸附加氢要困难及缓慢得多[31].根据以上推断, PS在Pd/SHMs表面的吸附加氢过程为:首先, 由于浓度差, PS分子扩散, 然后由于PS分子中不饱和键与催化剂中的活性中心之间存在一定的相互作用力, 使PS分子从溶液中扩散至催化剂表面并被吸附至活性位上进行加氢反应; PS分子中其他不饱和链段通过分子构型的转变而不断与活性位接触, 使PS分子加氢转化率不断提高; 由于吸附在活性位上的PS分子的双键数量的减少, 使其与活性位的作用力减弱; 与此同时, 溶液中其他未加氢的PS分子与吸附在活性位上的PS分子存在竞争吸附; 当PS分子的加氢转化率达到85%左右时, 加氢产物从活性位上脱附, 第一次吸附加氢结束; 当再增加反应时间或提高反应温度, 可促进部分加氢后的PS分子再进行二次吸附加氢达到更高的转化率.萃取后存在的不溶产物也具有一定的加氢度, 可能是部分加氢过程的时间过短, 有一部分PS分子在反应一段时间后才吸附在活性位上进行加氢, 导致其与催化剂活性金属组分接触时间过短, 没有足够时间使PS分子在催化剂表面进行构型的翻转, PS分子中少量的芳环经加氢反应后即从活性位上脱附分离, 导致部分PS的加氢转化率过低.
Overall conversion/% Conversion of extracted
polymer/%Conversion of undis
solved polymer/%38 85 15 57 83 21 69 86 28 表3 部分加氢产物分析
Table3. Analysis of partial hydrogenated PS2.1.2 PS吸附动力学模型的建立
对式(5)两边取对数, 可得:
式中,
$C{{_{\text{PS}}^{\text{a}}}^{*}}=\frac{4S}{\pi \cdot {{N}_{\text{A}}}\cdot V\cdot {{l}^{2}}}$ .将kd=0及式(2)代入式(1)中, 得:
一般而言, PS分子在固体表面的吸附形状近似为椭球形[45], 短轴设为l, 长轴设为h, 如图 2所示.被吸附时单个PS分子所占催化剂表面的表面积为: πl2/4;吸附在催化剂表面总的PS分子数为: NA·V·CPSa, 其中NA为阿伏伽德罗常数, V为溶液总体积.表面覆盖度θ定义为PS分子占据的吸附位点数与总的吸附位点的比例或者已吸附的PS分子与达到饱和吸附后PS分子占据的表面积的比值.由于活性金属Pd在催化剂表面分布均匀, 我们认为达到饱和吸附后PS分子可以占据整个催化剂表面.若催化剂的外表面积为S, 则θ的表达式为:
设:
将不同温度下的ka、CPS0以及CPSa*代入到式(4)中, 得到不同温度下的吸附动力学模型, 具体如式(8)至(12).
在推导前述吸附动力学模型时, 将吸附在催化剂表面的PS分子近似为椭球体, 根据公式(2)将CPSa*、S、V以及NA代入式中, 即可求得不同温度下椭球体的l值.聚合物分子在某一溶剂中的流体力学半径(RH)与分子量存在如下关系[46]:
式(4)可变为:
XAd实验值与动力学模型预测值比较如图 4所示, 由图可知, 在不同温度下的实验值与动力学模型预测值吻合很好, 说明该动力学模型能够很好地描述PS分子在催化剂表面的吸附过程.
根据文献报道的分子量为290000 g·mol-1的PS分子在混合溶剂中于不同温度时的RH值[46], 即可求得本文所采用的分子量为250000 g·mol-1的PS分子在不同温度时的RH值.吸附在固体表面的聚合物分子椭球体的h与RH以及l存在如下关系:
根据图 1描述的不同温度下PS的吸附曲线, 将在某一温度下不同吸附时间的XAd及CPSa*代入式(6)中, 即可求得不同吸附时间的f(t)值, 其中初始溶液浓度CPSa=0.2/(100×250000)=8×10-9 mol·mL-1.对f(t)及t作图, 根据斜率即可求得该温度下的ka.由不同时间的吸附数据可知, 在吸附实验2 h之内, 未达到饱和吸附, 可被认为是聚合物在固体表面的真实吸附过程, 因此采用2 h以前的吸附数据进行拟合结果更为准确.在不同吸附温度下拟合曲线如图 3所示.从图中可以看出实验值与拟合曲线吻合良好, 判定系数(R2)均在0.97以上, 拟合数据如表 1所示.
在t=0时, PS在催化剂表面的吸附量为0 (CPSa=0).对式(3)积分得吸附百分数XAd(物理意义在实验方法4.5节中说明)与时间t的关系方程为:
式中, CPSa为单位体积溶液催化剂上吸附的PS摩尔数; CPS为PS在溶液体相中的浓度; θ为PS在催化剂表面的覆盖度; ka和kd分别为吸附和脱附速率常数.由于未加氢前PS在固体表面为不可逆吸附, 脱附过程基本可忽略不计, 因而kd可近似为0.
由上式计算的RH、l及h值并列于表 1中.由表 1可知, 椭球的l值随温度的升高而降低, 而h值随温度的升高而升高. h值的大小可认为是聚合物在催化剂表面单层吸附时的吸附层厚度, 由图 1的吸附曲线可知, 在高温时会导致更高的CPSa*.根据l及h值的变化规律, 可对PS分子在低温及高温下在固体表面的吸附规律作定性的解释, 如图 5所示, l值随温度的升高而降低, 说明单个PS分子所占的表面积(A=πl2/4)随温度的升高而减小, 单层能够吸附更多的PS分子.同时, 温度的升高也有利于提高聚合物构型的转变, PS分子能够形成拉伸状的椭球体, 此结构在变换过程中, 溶剂中的PS分子与催化剂表面接触的几率增加, 从而提高最终催化剂的CPSa*.
文献研究结果表明[44], PS在催化剂表面的吸附速率方程如式(1)所示.
T/℃ 25 60 90 120 150 CPSa*/(mol·mL-1) 5.20×10-10 6.00×10-10 8.00×10-10 1.04×10-9 1.08×10-9 t/×103s 1.8 3.6 7.2 1.8 3.6 7.2 1.8 3.6 7.2 1.8 3.6 7.2 1.8 3.6 7.2 f(t) 4.11 12.2 — 2.38 3.54 13.95 1.60 3.70 9.10 1.38 2.01 4.65 1.30 2.47 4.80 ln f(t) 1.41 2.50 — 0.87 1.26 2.63 0.47 1.30 2.20 0.32 0.70 1.53 0.26 0.90 1.57 R2 0.987 0.984 0.977 0.996 0.971 ka/×10-5s-1 4.834 2.879 3.487 3.217 3.527 RH/nm 11.91 12.26 12.67 14.07 15.30 2RH/nm 23.82 24.52 25.34 28.14 30.60 A/nm2 424.9 368.2 276.2 212.4 204.6 l/nm 23.26 21.66 18.76 16.45 16.14 h/nm 24.99 31.44 46.30 82.29 109.85 表1 PS吸附动力学计算数据
Table1. Parameters of the adsorption kinetic model of PS2.1.1 不同温度下PS在催化剂上的吸附曲线
PS在不同温度的吸附曲线如图 1所示, 在较低温度(25 ℃)时, 吸附量随着吸附时间的延长而迅速升高, 在1 h后增加趋势逐渐变缓, 随着吸附时间的进一步延长, 吸附量基本保持不变, 说明PS在催化剂上已经达到饱和吸附.随着温度的升高, 达到饱和吸附的时间亦相应增加, 当温度升至150 ℃时, PS在催化剂上达到饱和吸附时所需时间增加至5 h左右, 且温度越高, 饱和吸附量(CPSa*)的值越大.聚合物吸附过程为吸热过程, 升高温度有利于提高CPSa*[43].另外, 在吸附时间较短时(0.5 h), 低温吸附量较高温吸附量要高, 这是由于温度较低时, PS分子的尺寸较小[36], 能够扩散到孔径较小的孔道中, 催化剂的比表面积有效利用率较高.但随着吸附时间的延长, 催化剂表面大部分被PS分子所覆盖, PS在催化剂表面的进一步吸附需要聚合物构型的重排, 而随着温度的升高, PS分子在催化剂表面构型变化的速率加快, 使溶剂中的聚合物分子与催化剂表面的接触几率增加, 导致CPSa*增加.
2.2.1 不同温度下PS加氢转化率曲线
在不同温度下PS加氢转化率随时间的变化规律如图 6所示, 当温度较低时(90 ℃), 转化率随反应时间的延长缓慢增加, 反应10 h后, PS的转化率仅为23%, 说明低温不利于PS的加氢反应.随着温度的升高, PS的转化率逐渐升高.在150 ℃时, 反应6 h后, PS转化率已达90%, 继续延长反应时间, 转化率仅略微升高.将温度进一步提高至180 ℃, 在2 h左右PS加氢转化率即达到95%以上, 然而当反应温度高于150 ℃时, PS分子容易发生断链等副反应.
2.2.2 加氢反应动力学模型
在前期试验中, 通过对比氢气压力从1~7 MPa时加氢度变化数据, 发现并无明显差异.由此认为当氢气压力为7 MPa且维持恒定时, 其反应级数b=0, 则CH2b为常数.因此, 式(16)可转变为:
为了系统研究PS非均相加氢的反应动力学, 我们采用幂函数型的方程描述反应过程的动力学并根据实验数据, 按照不同反应级数进行拟合, 得到拟合度最高的表达式来确定该反应的动力学方程及相应的反应级数. PS非均相催化加氢反应涉及的反应物为PS分子及氢气分子, 其动力学幂函数方程如式(15)所示.
则上式加氢反应过程平衡常数为:
由图 7可知, 在温度较低时(90及120 ℃), 不同反应级数对应的R2值均较高; 随着温度的升高, 0、2和3级反应拟合的R2值降低, 特别在180 ℃时, 按照0、2和3级反应回归得到的R2值均在0.9以下; 而按照1和1.5级反应拟合得到的不同温度下的R2值均在0.9以上, 拟合度较高.因此可以认为, 在PS加氢反应中, 苯环的加氢级数为1级或1.5级, 但就化学反应的本质而言, 一化学反应对应特定的反应级数, 因此需要从该反应的机理出发, 进一步确定实际的反应级数.
最终速率方程为:
由于催化剂用量与活性中心数目成正比, 催化剂用量越大, 则单位时间单位体积溶液反应速率越快.因此, 芳环加氢反应速率的物理意义为单位质量催化剂在单位反应时间内催化芳环加氢的摩尔数.则加氢反应速率方程为:
由于PS在催化剂表面需要长达数小时才能达到饱和吸附, 因此认为该步骤为吸附速率控制步骤[16, 17].因此, 总的速率方程为:
结合方程(25)、(26)和(27)可得:
……
式(32)为一级反应的速率方程的表达式.结合加氢机理及动力学拟合曲线, 最终认为PS在Pd/SHMs上进行的加氢反应为1级反应.速率常数与温度符合Arrhenius方程:
式中CAH6为完全饱和的芳环浓度, θAδ为被芳环占据的活性位分数.
式中: CA为溶液中芳环的浓度, CH2为溶液中氢气的浓度, a和b分别为芳环及氢气的反应级数, W为催化剂的质量.对上式进行变形可得:
因溶解在溶剂中的CH2会随氢压升高而增大, 而加氢反应过程通常在较高且恒定的氢气压力下进行, 由此认为CH2恒定为常数, 又因为加氢过程中的速率常数K10数值非常大, 上式分母可以近似为1.加氢反应速率方程近似为:
式中: θβ为未吸附氢气的活性位分数, θHβ为已吸附氢气的活性位分数.
以0级反应为例, 按式(18), 计算不同温度下的反应速率常数, X与Ccatt/CA0呈线性关系, 其中Ccat=10 g·L-1, CA0=20 g·L-1, 代入实验数据作图, 直线的斜率即为该温度下的速率常数.当反应级数为其他数值时, 亦可按照相应的表达式作图.按照不同反应级数所得拟合图如图 7所示, 相应的速率常数以及R2值列于表 2中(R2为线性相关系数的平方).比较不同反应级数的R2的大小, R2的数值越接近于1, 则对应的反应级数越接近真实反应级数.
方程(24)可变换为:
反应步骤Ⅲ至Ⅴ可合并为:
上述反应式中, β为吸附氢气的活性位, δ为吸附芳环的活性位, A为PS分子中的芳环, AHi为部分或完全饱和的芳环(如AH6为环己烷基).反应步骤(Ⅰ)为氢气在活性位上的吸附过程, 反应步骤(Ⅲ至Ⅴ)为芳环在活性位上的分步加氢过程, 反应步骤(Ⅵ)为加氢产物的脱附过程, 反应步骤(Ⅱ)为芳环在活性位上的吸附过程.
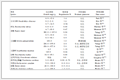 表2
按照不同反应级数的反应动力学方程的拟合结果
Table2.
Fitted parameters of the reaction kinetic equations according to different reaction orders
表2
按照不同反应级数的反应动力学方程的拟合结果
Table2.
Fitted parameters of the reaction kinetic equations according to different reaction orders
T/℃ 90 120 150 180 a=0 k′ 1.22×10-5 2.61×10-5 3.67×10-5 8.89×10-5 R2 0.970 0.971 0.702 0.689 a=1 k′ 7.16×10-7 2.31×10-6 8.76×10-6 3.32×10-5 R2 0.980 0.996 0.946 0.960 a=1.5 k′ 1.73×10-7 6.97×10-7 5.08×10-6 2.42×10-5 R2 0.983 0.999 0.994 0.958 a=2 k′ 4.2×10-8 2.12×10-7 3.27×10-6 1.97×10-5 R2 0.986 0.995 0.977 0.854 a=3 k′ 2.48×10-9 1.99×10-8 1.71×10-6 1.69×10-7 R2 0.989 0.971 0.846 0.612 表2 按照不同反应级数的反应动力学方程的拟合结果
Table2. Fitted parameters of the reaction kinetic equations according to different reaction orders在苯环加氢过程中, 当芳环吸附到活性位表面后, 其加氢反应过程非常迅速, 可近似为平衡过程, 由于PS分子中的不饱和键与催化剂中的活性中心之间存在一定的相互作用力, 苯环在加氢后由于双键数量的减少, 使其与活性位的作用力减弱, 迅速脱附, 因此部分加氢产物所占据的活性位分数可忽略不计.则活性位分数平衡方程近似为:
假设芳环的反应级数a分别为0、1、1.5、2和3, 对式(17)积分分别可得:
式中, θδ为未吸附苯环的活性位分数, CA为反应溶液中苯环的浓度.
其他反应步骤为准平衡步骤, 则反应步骤(Ⅰ)的平衡常数为:
从微观角度上, PS非均相加氢过程涉及PS分子和氢气分子从液相中扩散至催化剂微球表面, 然后扩散至孔道内部与活性位接触, PS分子及氢气分子同时被吸附到活性位表面而活化, PS加氢过程可分为以下几个步骤:
式中: Ccat为单位体积溶液中催化剂的质量.
速率方程可转化为:
式中, nA=CAV, Ccat=W/V.
以ln k对(-1/RT)作图, 斜率即为该反应的活化能, 如图 8所示.拟合直线的R2为0.987, 说明该动力学方程很好地反映了以Pd/SHMs为催化剂催化PS加氢反应动力学的实质.计算该反应的活化能为58.3 kJ·mol-1, 略低于所报道的以Pd/BaSO4为催化剂对PS催化加氢的活化能(59.6 kJ·mol-1)[15].
3 结论
系统研究了PS在Pd/SHMs上的吸附和加氢反应动力学, 推导出了在不同温度下PS的吸附动力学模型, 合理地解释了不同温度下PS分子在催化剂表面的吸附行为.由PS在催化剂表面的椭球型吸附模型可知, 温度升高有利于聚合物构型的转变, PS分子易形成拉伸状的椭球体, 极大增加了PS分子与催化剂表面接触的几率, 从而增大饱和吸附量.另外, 通过幂函数动力学计算及加氢机理推导的方法, 确定了本反应体系PS非均相催化反应级数为1级, 活化能为58.3 kJ·mol-1.对PS的部分加氢产物分析可知, PS的部分加氢产物由较高加氢转化率和较低加氢转化率的PS组成, 说明PS非均相加氢服从“Blocky”机理.本工作为其他类似不饱和聚合物在非均相催化剂上的吸附及加氢过程提供了研究基础.
4 实验部分
4.1 材料
采用以实验室合成的表面具有贯穿大孔的二氧化硅空心微球为载体制备的负载型催化剂Pd/SHMs作为PS加氢催化剂[42], 其粒径为5~15 μm, 比表面积325 m2/g, 孔径560 nm左右, Pd负载量5 wt%.采用Tecnai G2 F20型场发射透射电子显微镜对催化剂进行表征并统计了Pd颗粒尺寸(如图 9所示), 从图中可以看出Pd颗粒分布比较均匀, 粒径尺寸大约在10 nm. PS分子量为250000 g·mol-1, J & k chemical所购.实验中所用溶剂均为分析纯. PS加氢反应采用威海源城石化设备有限公司制造的高压加氢反应釜.紫外-可见分光光度计采用中国普析通用仪器公司生产的TU-1810分光光度计.
4.2 PS加氢反应
首先, 将1.60 g PS颗粒加入到20 mL四氢呋喃及80 mL环己烷的混合溶剂中, 磁力搅拌至PS完全溶解后, 转移至反应釜中, 同时加入1.0 g催化剂; 密封反应釜, 设置搅拌速率1200 r/min、不同反应时间和反应温度(分别为90、120、150及180 ℃)后, 开始对反应釜进行加热; 当加热到设定温度后, 在1 min内向反应体系中充入7 MPa氢气至反应压力, 反应自动开始, 开始搅拌、计时, 并在反应过程中不断补充氢气维持氢压在7.0±0.1 MPa; 反应结束后, 离心分离回收催化剂.加氢产物采用乙醇萃取后在70 ℃真空烘箱中烘干至恒重, 对加氢产物进行加氢转化率分析.
4.3 PS吸附实验
与实际催化加氢反应过程一致, 但在吸附行为研究中不向反应体系通入氢气.具体过程如下:将PS浓度为2.0 g·L-1的20 mL四氢呋喃与80 mL环己烷的混合溶液加入到加氢反应釜中, 密封; 对反应器升温至设定吸附温度(分别为25、60、90、120及150 ℃), 加入1.0 g Pd/SHMs催化剂, 开始搅拌并计时, 进行吸附反应; 当吸附反应结束后, 停止对反应器加热和搅拌, 通入冷却水迅速降温, 取出胶液, 离心分离, 取上层清液进行分析.
4.4 PS部分加氢产物分析
将0.5 g部分加氢后的PS溶解至20 mL正己烷中, 充分搅拌溶解5 h, 完全溶解后静置30 min, 使不溶物沉于底部.然后以移液管将上层清液取出, 完全烘干除去溶剂得到双键含量较少的聚合物, 分析其具体的加氢转化率; 不溶物采用正己烷溶液洗涤数次后, 烘干得到双键含量较多的聚合物, 测定其具体的加氢转化率.
4.5 分析表征方法
其中HD为PS的加氢转化率, CA为加氢后胶液浓度, CA0为加氢前胶液浓度.胶液浓度测量利用浓度与吸光度的标准曲线(图 10).
PS加氢转化率按照如下公式进行计算:
PS溶液浓度通过紫外可见光谱法测得.测定方法为:一系列已知浓度的PS溶液在261.5 nm处的吸光度, 绘制浓度与吸光度的标准曲线, 如图 10所示.然后测定未知PS溶液的吸光度, 对照标准曲线, 得到该溶液中PS的准确浓度.计算吸附百分数(XAd):
其中CPS0为初始胶液中的PS浓度, CPS为吸附后溶液中的PS浓度.达到饱和吸附时的XAd乘以CPS0即为在该温度下的饱和吸附量(CPSa*).
-
-
[1]
Singha, N. K.; Bhattacharjee, S.; Sivaram, S. Rubber Chem. Technol. 1997, 70, 311.
-
[2]
Xu, Z. D.; Hadjichristidis, N.; Carella, J. M.; Fetters, L. J. Macromolecules 1983, 16, 925. doi: 10.1021/ma00240a019
-
[3]
Dondos, A.; Staikos, G. Colloid Polym. Sci. 1995, 273, 626. doi: 10.1007/BF00652254
-
[4]
Garcia Escribiano, P.; Canovas, M. J.; Ojeda, M. C.; Del Rio, C.; Sanchez, F.; Acosta, J. L. Polym. Int. 2011, 60, 493. doi: 10.1002/pi.v60.3
-
[5]
Wei, Z. L.; Wu, J. L.; Pan, Q. M.; Rempel, G. L. Macromol. Rapid Commun. 2005, 26, 1768. doi: 10.1002/(ISSN)1521-3927
-
[6]
Monroy-Barreto, M.; Acosta, J. L.; Del Rio, C.; Ojeda, M. C.; Munoz, M.; Aguilar, J. C. J. Power Sources 2010, 195, 8052. doi: 10.1016/j.jpowsour.2010.06.105
-
[7]
金美花, 廖明义, 翟锦, 江雷, 化学学报, 2008, 66, 145. http://sioc-journal.cn/Jwk_hxxb/CN/abstract/abstract330950.shtmlJin, M.; Liao, M.; Zhai, J.; Jiang, L. Acta Chim. Sinica 2008, 66, 145. http://sioc-journal.cn/Jwk_hxxb/CN/abstract/abstract330950.shtml
-
[8]
徐立新, 李为立, 杨慕杰, 化学学报, 2007, 65, 1917. http://sioc-journal.cn/Jwk_hxxb/CN/abstract/abstract329626.shtmlXu, L.; Li, W.; Yang, M. Acta Chim. Sinica 2007, 65, 1917. http://sioc-journal.cn/Jwk_hxxb/CN/abstract/abstract329626.shtml
-
[9]
张淑芳, 白赢, 彭家建, 胡应乾, 来国桥, 化学进展, 2013, 25, 707.Zhang, S.; Bai, Y.; Peng, J.; Hu, Y.; Lai, G. Prog. Chem. 2013, 25, 707.
-
[10]
Przybyszewska, M.; Zaborski, M. Composite Interfaces 2009, 16, 131. doi: 10.1163/156855409X402920
-
[11]
Yoon, K.; Kim, K. O.; Schaefer, M.; Yoon, D. Y. Polymer 2012, 53, 2290. doi: 10.1016/j.polymer.2012.02.047
-
[12]
Choi, M.; Kim, Y.; Ha, C. Prog. Polym. Sci. 2008, 33, 581. doi: 10.1016/j.progpolymsci.2007.11.004
-
[13]
Gehlsen, M. D.; Bates, F. S. Macromolecules 1993, 26, 4122. doi: 10.1021/ma00068a009
-
[14]
黄辉, 樊一帆, 陶士英, 高浩其, 化工新型材料, 2013, 41, 178.Huang, H.; Fan, Y.; Tao, S.; Gao, H. New Chem. Mater. 2013, 41, 178.
-
[15]
Ness, J. S.; Brodil, J. C.; Bates, F. S.; Hahn, S. F.; Hucul, D. A.; Hillmyer, M. A. Macromolecules 2001, 35, 602.
-
[16]
Dong, L. B.; Turgman-Cohen, S.; Roberts, G. W.; Kiserow, D. J. Ind. Eng. Chem. Res. 2010, 49, 11280. doi: 10.1021/ie1011905
-
[17]
Xu, D.; Carbonell, R. G.; Kiserow, D. J.; Roberts, G. W. Ind. Eng. Chem. Res. 2003, 42, 3509. doi: 10.1021/ie0301841
-
[18]
Hucul, D. A.; Hahn, S. F. Adv. Mater. 2000, 12, 1855. doi: 10.1002/(ISSN)1521-4095
-
[19]
Aylward, F.; Sawistowka, M.; Arthur, F.; Robert, C. B.; Shirley, H. Chem. Rev. 1965, 65, 51. doi: 10.1021/cr60233a002
-
[20]
Parent, J. S.; Mcmanus, N. T.; Rempel, G. L. Ind. Eng. Chem. Res. 1996, 35, 4417. doi: 10.1021/ie9506680
-
[21]
Martin, P.; Mcmanus, N. T.; Rempel, G. L. J. Mol. Catal. A: Chem. 1997, 126, 115. doi: 10.1016/S1381-1169(97)00102-7
-
[22]
Bhattacharjee, S.; Bhowmick, A. K.; Avasthi, B. N. J. Polym. Sci. Part A: Polym. Chem. 1992, 30, 471. doi: 10.1002/pola.1992.080300314
-
[23]
Bond, G. C. Heterogeneous Catalysis: Principles and Applications, 2nd Ed., Clarendon Press, Oxford, 1987, p. 120.
-
[24]
Bussard, A.; Dooley, K. M. AIChE J. 2008, 54, 1064. doi: 10.1002/(ISSN)1547-5905
-
[25]
周宏勇, 强明辉, 李军章, 李云庆, 王家喜, 高分子材料科学与工程, 2011, 27, 73.Zhou, H.; Qiang, M.; Li, J.; Li, Y.; Wang, J. Polym. Mater. Sci. Eng. 2011, 27, 73.
-
[26]
Almusaiteer, K. A. Top. Catal. 2012, 55, 498. doi: 10.1007/s11244-012-9821-3
-
[27]
Hutchings, G. J. J. Mater. Chem. 2009, 19, 1222. doi: 10.1039/B812300B
-
[28]
Fang, F.; Satulovsky, J.; Szleifer, I. Biophys. J. 2005, 89, 1516. doi: 10.1529/biophysj.104.055079
-
[29]
Rosedale, J. H.; Bates, F. S. J. Am. Chem. Soc. 1988, 110, 3542. doi: 10.1021/ja00219a032
-
[30]
黄辉, 周俊涛, 应勤荣, 陶士英, 现代化工, 2014, 34, 70.Huang, H.; Zhou, J.; Ying, Q.; Tao, S. Mod. Chem. Ind. 2014, 34, 70.
-
[31]
Cassano, G. A.; Vallés, E. M.; Quinzani, L. M. Polymer 1998, 39, 5573. doi: 10.1016/S0032-3861(97)10080-5
-
[32]
Tsukagoshi, T.; Kondo, Y.; Yoshino, N. Colloids Surf. B-Biointerfaces 2007, 54, 101. doi: 10.1016/j.colsurfb.2006.10.004
-
[33]
Linse, P.; Kallrot, N. Macromolecules 2010, 43, 2054. doi: 10.1021/ma902338m
-
[34]
Kawaguchi, M.; Anada, S.; Nishikawa, K.; Kurata, N. Macromolecules 1992, 25, 1588. doi: 10.1021/ma00031a035
-
[35]
Kawaguchi, M.; Sakata, Y.; Anada, S.; Kato, T.; Takahashi, A. Langmuir 1994, 10, 538. doi: 10.1021/la00014a033
-
[36]
Rybicka, J.; Sikorski, A. Macromol. Theory Simul. 2010, 19, 135.
-
[37]
Scheutjens, J. M. H. M.; Fleer, G. J. J. Phys. Chem. 1979, 83, 1619. doi: 10.1021/j100475a012
-
[38]
Scheutjens, J. M. H. M.; Fleer, G. J. J. Phys. Chem. 1980, 84, 178. doi: 10.1021/j100439a011
-
[39]
Doi, Y.; Yano, A.; Soga, K.; Burfield, D. R. Macromolecules 1986, 19, 2409. doi: 10.1021/ma00163a013
-
[40]
Tangthongkul, R.; Prasassarakich, P.; Mcmanus, N. T.; Rempel, G. L. J. Appl. Polym. Sci. 2004, 91, 3259. doi: 10.1002/(ISSN)1097-4628
-
[41]
Hinchiranan, N.; Charmondusit, K.; Prasassarakich, P.; Rempel, G. L. J. Appl. Polym. Sci. 2006, 100, 4219. doi: 10.1002/(ISSN)1097-4628
-
[42]
Pan, D.; Shi, G.; Zhang, T.; Yuan, P.; Fan, Y.; Bao, X. J. Mater. Chem. A 2013, 1, 9597. doi: 10.1039/c3ta11824j
-
[43]
Dijt, J. C.; Cohen Stuart, M. A.; Fleer, G. J. Macromolecules 1994, 27, 3207. doi: 10.1021/ma00090a014
-
[44]
Kislenko, V. N.; Berlin, A. A.; Kawaguchi, M.; Kato, T. Langmuir 1996, 12, 768. doi: 10.1021/la950478u
-
[45]
Tóth, J. Adsorption: Theory, Modeling, and Analysis, Marcel Dekker, New York, 2002, p. 26.
-
[46]
Whittier, R. E. MS Thesis, North Carolina State University, Raleigh, 2004.
-
[1]
-
表 1 PS吸附动力学计算数据
Table 1. Parameters of the adsorption kinetic model of PS
T/℃ 25 60 90 120 150 CPSa*/(mol·mL-1) 5.20×10-10 6.00×10-10 8.00×10-10 1.04×10-9 1.08×10-9 t/×103s 1.8 3.6 7.2 1.8 3.6 7.2 1.8 3.6 7.2 1.8 3.6 7.2 1.8 3.6 7.2 f(t) 4.11 12.2 — 2.38 3.54 13.95 1.60 3.70 9.10 1.38 2.01 4.65 1.30 2.47 4.80 ln f(t) 1.41 2.50 — 0.87 1.26 2.63 0.47 1.30 2.20 0.32 0.70 1.53 0.26 0.90 1.57 R2 0.987 0.984 0.977 0.996 0.971 ka/×10-5s-1 4.834 2.879 3.487 3.217 3.527 RH/nm 11.91 12.26 12.67 14.07 15.30 2RH/nm 23.82 24.52 25.34 28.14 30.60 A/nm2 424.9 368.2 276.2 212.4 204.6 l/nm 23.26 21.66 18.76 16.45 16.14 h/nm 24.99 31.44 46.30 82.29 109.85 表 2 按照不同反应级数的反应动力学方程的拟合结果
Table 2. Fitted parameters of the reaction kinetic equations according to different reaction orders
T/℃ 90 120 150 180 a=0 k′ 1.22×10-5 2.61×10-5 3.67×10-5 8.89×10-5 R2 0.970 0.971 0.702 0.689 a=1 k′ 7.16×10-7 2.31×10-6 8.76×10-6 3.32×10-5 R2 0.980 0.996 0.946 0.960 a=1.5 k′ 1.73×10-7 6.97×10-7 5.08×10-6 2.42×10-5 R2 0.983 0.999 0.994 0.958 a=2 k′ 4.2×10-8 2.12×10-7 3.27×10-6 1.97×10-5 R2 0.986 0.995 0.977 0.854 a=3 k′ 2.48×10-9 1.99×10-8 1.71×10-6 1.69×10-7 R2 0.989 0.971 0.846 0.612 表 3 部分加氢产物分析
Table 3. Analysis of partial hydrogenated PS
Overall conversion/% Conversion of extracted
polymer/%Conversion of undis
solved polymer/%38 85 15 57 83 21 69 86 28 -

 扫一扫看文章
扫一扫看文章
计量
- PDF下载量: 0
- 文章访问数: 2562
- HTML全文浏览量: 566












 下载:
下载:









 下载:
下载:

