图 1
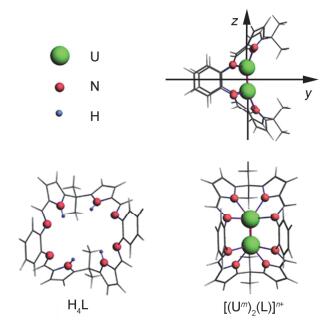
用Priroda程序在PBE/B-Ⅰ方法下优化的H4L配体和[(Um)2(L)]n+ (m＝Ⅱ~Ⅳ, n＝0~4) 配合物结构, 其中分别给出了配合物的侧视图(上)和正视图(下)
Figure 1.
Optimized structures (left) of the ligand H4L and the complexes [(Um)2(L)]n+ (m＝Ⅱ~Ⅳ, n＝0~4) in Priroda codes where side-on (top) and face-on (bottom) views are shown
引用本文:
陈方园, 曲宁, 吴群燕, 张红星, 石伟群, 潘清江. 二价双核铀聚吡咯配合物结构设计和铀-铀多重键的理论研究[J]. 化学学报,
2017, 75(5): 457-463.
doi:
10.6023/A17010008
Citation: Chen Fangyuan, Qu Ning, Wu Qunyan, Zhang Hongxing, Shi Weiqun, Pan Qingjiang. Structures and Uranium-Uranium Multiple Bond of Binuclear Divalent Uranium Complex of Pyrrolic Schiff-base Macrocycle: a Relativistic DFT Probe[J]. Acta Chimica Sinica, 2017, 75(5): 457-463. doi: 10.6023/A17010008
Citation: Chen Fangyuan, Qu Ning, Wu Qunyan, Zhang Hongxing, Shi Weiqun, Pan Qingjiang. Structures and Uranium-Uranium Multiple Bond of Binuclear Divalent Uranium Complex of Pyrrolic Schiff-base Macrocycle: a Relativistic DFT Probe[J]. Acta Chimica Sinica, 2017, 75(5): 457-463. doi: 10.6023/A17010008
二价双核铀聚吡咯配合物结构设计和铀-铀多重键的理论研究
摘要:
经三十余年努力，二价铀溶液化学于近年取得突破性进展，Evans和Meyer等成功获得两个可通过X-ray晶体衍射表征结构的有机金属铀（Ⅱ）配合物.为进一步拓展UⅡ配合物化学和探索可能存在的金属多重键，设计双核配合物[（UⅡ）2（L）]（L为八齿氮供体低聚吡咯大环四价阴离子），并使用相对论密度泛函理论优化其可能的电子自旋态异构体结构和计算相关性质.结果表明，[（UⅡ）2（L）]具有三重态基态，其电子组态为π4σ2δ2；U（5f）原子轨道对高占据分子轨道有重要贡献；它的U—U键长为2.33Å、Mayer键级为3.89和对应的伸缩振动频率为259 cm-1，被指认为U—U弱四重键.这一结论与QTAIM（quantum theory of atoms in molecule）的U—U键临界点处的电子/能量密度拓扑分析结果相一致.与不同氧化态铀同类物[（Um）2（L）]n+（m=Ⅲ，n=2；m=Ⅳ，n=4）比较显示，随着铀氧化态增大，U—U距离增长、键级变小、伸缩振动频率变小，金属铀电子自旋密度与常规预期值的差值（∆SU）增大；结合分子轨道和QTAIM参数分析，发现金属氧化态可以调控配体和金属轨道能级匹配程度和改变金属-金属多重键.
-
关键词:
- 双核UⅡ聚吡咯配合物
- / 电子结构
- / 铀-铀多重键
- / QTAIM拓扑分析
- / 相对论密度泛函理论
English
Structures and Uranium-Uranium Multiple Bond of Binuclear Divalent Uranium Complex of Pyrrolic Schiff-base Macrocycle: a Relativistic DFT Probe
Abstract:
Although attempts to synthesize divalent uranium molecules were begun three decades ago, molecular U(Ⅱ) species isolable in solution have been not achieved until recent years. In 2013, Evans and co-workers synthesized the first U(Ⅱ) complex, [U(Cp')3]·[K(2, 2, 2-cryptand)] (Cp'=C5H4SiMe3) via flash reduction, that was suitable for X-ray crystal diffraction characterization. A year later, the group of Meyer obtained another divalent uranium complex, [U((Ad, MeArO)3mes)]·[K(2, 2, 2-cryptand)] employing their particularly interesting tris(aryloxide) arene ligand. The 5f36d1 and 5f4 ground states were assigned to these two complexes, respectively, by the jointed experimental/theoretical studies. It was demonstrated that the ligand significantly affect the nature of the ground state of divalent uranium complex by tuning the energetic separation of the 5f and 6d orbitals. Therefore, careful selection of ligand makes it possible to have access to +Ⅱ oxidation state of uranium and prepare new UⅡ complex. A flexible octadentate polypyrrollic Schiff-base macrocycle (H4L) has been developed to complex a variety of metals such as actinides, rare earth and transition metals that show a wide range of size and diverse oxidation states. Both mono-and bimetallic complexes featured with an intriguing "Pacman-like" structure were obtained. For example, the reaction of H4L with a trivalent uranium precursor [(UⅢ)Ⅰ3(THF)4] yielded a neutral [(UⅣ)(L)] complex, where the uranium ion was determined by the single crystal X-ray diffraction to be situated inside the ligand mouth and held by eight nitrogen atoms together. The +Ⅳ oxidation state was assigned to the uranium by presuming dihydrogen elimination. Considering the flexibility, tetravalent-anion nature as well as capability of accommodating bimetallic ions and stabilizing various oxidation states of uranium (e.g. Ⅲ~Ⅵ complexes have been found so far) that the polypyrrolic ligand has exhibited in previously synthesized complexes, two divalent uranium ions would be likely complexated by the ligand to generate a complex, [(UⅡ)2(L)]. In addition to enriching the coordination chemistry of U(Ⅱ), it is also a good example to explore electronic structures of the low-valent uranium complex and unravel the uranium-uranium multiple bonding nature. Although many theoretical studies have explored uranium complexes, the study focusing on the divalent diuranium complex of a single macrocyclic ligand remains rare. In the work, a relativistic density functional theory has been employed to investigate [(UⅡ)2(L)]. The structures in electron spin states (singlet, triplet, quintet, septet and nonet) were optimized. Short distances of U—U (2.32~2.67 Å), large bond order (2.95~3.90) and high stretching vibrational frequencies (180~263 cm-1) were calculated. Energetic calculations find that its triplet state is the ground state. It has the electronic configuration of π4σ2δ2, primarily contributed by U(5f) character. Structural and molecular-orbital analyses suggest a slightly weak uranium-uranium quadruple bond, which is confirmed by the quantum theory of atoms in molecule (QTAIM) calculations. Further comparison with analogues [(UⅢ)2(L)]2+ and [(UⅣ)2(L)]4+ was also addressed. It is found that the uranium oxidation state is able to tune the energetic matching between the highest-energy occupied orbital of ligand and the adjacent low-energy metal-based orbital, as well as correlates with the electron transfer between metal and ligand and the diuranium multiple bond number.
-
1 引言
铀是核能生产、核武器制造和核废料处理的最重要元素之一[1].目前已知铀的氧化态包括Ⅱ~Ⅵ.相比其它氧化态, 在溶液化学中稳定存在的二价铀分子配合物少之又少[2~4].虽然从20世纪80年代就开始二价铀化合物溶液化学(配位化学和有机金属化学)研究, 但是直到四年前才合成第一个已知结构的二价铀配合物.即, Evans课题组2013年采用低温还原有机金属铀化合物[UⅢ(Cp′)3] (Cp′＝C5H4SiMe3)方法成功制备可适用于X-ray晶体衍射技术表征的二价铀金属配合物[UⅡ(Cp′)3]•[K(2, 2, 2-cryptand)][3]; 文中的理论计算和实验表征共同揭示该配合物具有5f36d1的基态电子组态, 与以前发现的二价稀土配合物4fn5d1基态电子结构类似, 但不同于二价铀离子5f4结构[5].一年后, 德国Meyer教授及其合作者使用类似合成方法、采用他们独特的tris(aryloxide) arene类配体(Ad, MeArO)3mes得到配合物[UⅡ((Ad, MeArO)3mes)]•[K(2, 2, 2-cryptand)][4]; 有趣的是, 这个化合物基态电子组态为5f4.以上研究表明, 配体能够调控5f和6d轨道能级, 影响二价铀配合物基态电子结构, 同时它也是稳定二价铀离子的重要因素之一[2].因此, 选择适当配体有望能够合成更多的新型二价铀配合物.
柔性八齿氮配位低聚吡咯配体大环(H4L, 图 1)分别由Sessler教授[6]和Love教授[7]课题组合成.后者进一步使用该配体成功络合种类多样和氧化态各异的金属离子, 包括锕系、稀土和过渡金属, 获得具有“Pacman”结构的单核和双核金属配合物[8~13].值得指出的是, 这些配合物中涵盖从Ⅲ~Ⅳ的金属铀.就配位结构而言, 大环配体既可使用它的两个N4供体空穴同时配位两个金属离子, 也可只用一个N4空穴配位一个金属而另一个空穴空置, 还可以直接由八个N包裹一个金属离子.例如, 通过H4L和[(UⅢ)Ⅰ3(THF)4]反应合成[(UⅣ)(L)]配合物; X-ray晶体衍射表明UⅣ同时被八个N原子配位[10].既然H4L低聚吡咯大环在配合物中形成负四价阴离子、具有柔软结构特性且可以同时络合两个金属离子和稳定各种金属氧化态(已知有UⅢ~UⅥ配合物), 那么可否使用该配体同时络合两个二价铀金属离子呢？配合物[(UⅡ)2(L)]的研究不仅可以丰富二价铀配位化学和其几何/电子结构, 也为探索铀-铀金属多重键提供很好的模型化合物.
图 1
用Priroda程序在PBE/B-Ⅰ方法下优化的H4L配体和[(Um)2(L)]n+ (m＝Ⅱ~Ⅳ, n＝0~4) 配合物结构, 其中分别给出了配合物的侧视图(上)和正视图(下)
Figure 1.
Optimized structures (left) of the ligand H4L and the complexes [(Um)2(L)]n+ (m＝Ⅱ~Ⅳ, n＝0~4) in Priroda codes where side-on (top) and face-on (bottom) views are shown
因其在乏燃料、核废料等中的存在形式, 且极易溶于水对环境造成很大的污染, 各种氧化态铀化合物溶液化学研究非常重要.本文设计的双核铀聚吡咯配合物, 通过对其稳定性和化学键性质探索, 将对铀配合物的分离化学、降低核废料对环境的污染等方面的实验开展具有理论指导意义.
2 计算方法
理论设计和计算双核金属铀配合物[(Um)2(L)]n+ (m＝Ⅱ, n＝0; m＝Ⅲ, n＝2; m＝Ⅳ, n＝4).最近, 潘清江课题组[14]报道了三价配合物多样化的空间异构体结构, 鉴于本文目的是探索低价化合物电子性质(尤其是二价化合物)和铀-铀金属多重键, 所以我们将关注两个铀原子通过z轴的空间异构体, 如图 1所示.由于低氧化态铀含多个5f和/或6d电子, 其双核配合物可形成多种电子自旋态.例如, [(UⅡ)2(L)]包括从单重态到九重态共计五种可能电子自旋态.本文将优化二价和四价配合物所有电子自旋态结构, 并与三价化合物的进行比较讨论.
采用Priroda程序优化配合物在各种自旋态下的“异构体”结构.该程序运用全电子四分量标量相对论(AE)哈密顿[15], 采用广义梯度近似的PBE (Perdew-Burke-Ernzerh)泛函[16]和全电子correlation-consistent Gaussian基组(用B-Ⅰ表示).在优化结构基础上进行频率计算, 未得到任何虚频表明优化的结构是稳定构型.
进而, 使用ADF2014程序包[17]探索双核铀配合物基态电子性质.为描述配合物的分子环境, 计算中采用COSMO (Conductor-like Screening Model)[18]模型, 选用THF溶剂, 介电常数为7.58;模型中Klamt半径为U＝1.70 Å、N＝1.83 Å、C＝2.00 Å和H＝1.30 Å[14, 18~20]. ADF计算中使用标量相对论ZORA (Zero Order Regular Approximation)哈密顿[21]、Slater型TZP基组(B-Ⅱ)和PBE泛函, 并对U和N/C分别采用冻结1s~4f和1s核轨道近似.分别使用ADF和Priroda程序计算Mayer键级和Mulliken电荷, 前者计算还得到原子轨道布居.为进一步考察泛函选择对这些计算结果的影响, 还使用ADF程序中的杂化泛函B3LYP(包含20% HF exchange)和mPW1PW(42.8%)进行计算.最后, 采用ADF程序进行Quantum Theory of Atoms in Molecule (QTAIM)计算, 得到U—U键临界点(Bond critical point)的电子密度ρ(r)和拉普拉斯密度∇2ρ(r); 同时采用Gaussian09程序[22], 运用6-31G (d)基组、B3LYP泛函方法、其中U原子使用准相对论效应的小核赝势ECP60MWB[23], 结合Multiwfn软件分析得到能量密度H(r)[24].
3 结果与讨论
3.1 几何结构和相对稳定性
在表 1中, 列出了优化得到配合物[(Um)2(L)]n+ (m＝Ⅱ~Ⅳ, n＝0~4) 所有电子自旋态的U—U键长、键级、伸缩振动频率等信息, 并于图 1中给出其结构图.可以看出, 二价铀配合物的U—U键长从单重态的2.32 Å增长至九重态的2.67 Å, 对应的Mayer键级则从3.90逐渐减少至2.95;同时, 频率计算发现U—U伸缩振动在180~263 cm–1范围.通过这些数据可以推断出二价U—U之间具有金属-金属多重键, 其强度介于三重键和四重键之间.其对应的优化四价铀配合物的单重态、三重态和五重态结构中的U—U键长分别为2.63、2.64和2.72 Å, 其对应的键级(2.28~2.33) 和U—U伸缩振动频率(140~156 cm–1); 两个UⅣ金属键可能具有双重键性质.很明显, 三价铀配合物的各自旋态结构中的U—U键长(2.43~2.62 Å)、键级(3.08~3.18) 和伸缩振动频率(188~220 cm–1)表明其U—U键具有三重键特征.到目前为止, 虽然实验已合成一些含U—M (M为过渡金属和主族金属)相互作用的配合物[25~29], 但尚未发现含有U—U键的配合物.另外, 理论计算对双核UⅢ配合物(分子)的研究较多, 如U2ⅢX6和[U2ⅢX8]2– (X＝F, Cl, OH, NH2和CH3)[30, 31], 指认了其U—U三重键本质, 但是对二价和四价双核铀配合物的报道却很少[32, 33].
表 1
计算配合物在不同电子自旋态(ESS)下U—U的键长(D, Å)、键级(BO)、伸缩振动频率(ν, cm–1)和铀原子电子自旋密度(SU), 以及它们的相对能量(kJ/mol)a
Table 1.
Calculated U—U distances (D, Å), bond orders (BO), stretching vibrational frequencies (ν, cm–1) and electron-spin density (SU) of uranium atoms for diuranium complexes in various electron-spin states (ESS), together with the relative energies (kJ/mol)a
Complex ESS D ν BO SU QU ΔE ΔE0 [(UⅡ)2(L)] nonet 2.668 180 2.95 3.789 1.055 68.0 64.9 septet 2.517 196 3.52 2.958 1.078 42.5 40.1 quintet 2.412 235 3.76 1.916 1.087 27.7 25.8 triplet 2.332 259 3.89 0.939 1.067 0.0 0.0 singlet 2.324 263 3.90 0.000 1.069 24.4 23.9 [(UⅢ)2(L)]2+ septet 2.622 188 3.08 3.001 1.372 26.9 26.9 quintet 2.506 201 3.14 2.045 1.373 2.8 2.3 triplet 2.474 214 3.18 1.073 1.380 0.0 0.0 singlet 2.426 220 3.17 0.000 1.349 11.9 12.3 [(UⅣ)2(L)]4+ quintet 2.720 140 2.28 2.103 1.541 0.0 0.0 triplet 2.641 149 2.33 1.240 1.516 11.8 11.8 singlet 2.627 156 2.31 0.000 1.528 31.8 31.8 a ΔE denotes the total energy and ΔE0 includes the zero-point vibration energy, which were obtained by subtracting the respective ground-state energy. Trivalent complexes were reported in our previous work[14]. 表 1 计算配合物在不同电子自旋态(ESS)下U—U的键长(D, Å)、键级(BO)、伸缩振动频率(ν, cm–1)和铀原子电子自旋密度(SU), 以及它们的相对能量(kJ/mol)a
Table 1. Calculated U—U distances (D, Å), bond orders (BO), stretching vibrational frequencies (ν, cm–1) and electron-spin density (SU) of uranium atoms for diuranium complexes in various electron-spin states (ESS), together with the relative energies (kJ/mol)a表 1和图 1给出了各种电子自旋态异构体的相对能量.可以看出, 二价铀配合物的三重态能量最低, 为基态.它比对应的其它态的总能量(∆E)低24~68 kJ/mol; 包括零点振动能的能量(∆E0)表现出同样的趋势.四价铀配合物的五重态为基态, 比其单重态和三重态分别低32和12 kJ/mol (∆E).能量计算表明三价铀配合物的三重态的能量最低, 但是仅仅比其五重态低3 kJ/mol, 说明这两个电子自旋态很容易在室温下相互转换.以二价铀配合物为例, 使用不同泛函(Pri: B3LYP)和不同程序(ADF: PBE和B3LYP)计算其各个自旋态的相对能量(见支持信息表S1), 得到结果均表明三重态为二价配合物的基态.最近Truhlar教授课题组[34]发展的Minnesota系列泛函能够在较低计算资源消耗时得到与高级别波函数理论方法[如CCSD(T)]一样准确的体系能量, 有望在将来用于双核铀体系的计算.
考虑到理论方法对化学键强度的影响, 我们使用ADF程序计算上述三种配合物基态的U—U和U—N键级(表 2).不难看出, ADF计算的二价铀配合物U—U键的Mayer键级为4.80, 远大于Priroda得到的3.89;而前者得到U—N平均键级为0.39, 小于后者(0.51).可以推断出, 由于两种理论级别采用不同基组(分别用Gaussian和Slater基组)和相对论哈密顿(AE和ZORA), 所以即使都运用同样的泛函(PBE)和键级Partition方法(Mayer)也导致键级数据的差别.即在ADF计算中趋于高估电子密度在U—U间的分布, 而使得U—N键级相对较小; 而Priroda则是倾向于电子在U—N间的分布, 使得U—U键级相对较小.同样的, ADF和Priroda计算的三价铀配合物的U—U和U—N键级也有很大差别, 显然还是电子密度分布所致.有趣的是, 四价铀配合物的U—U键级在两种理论级别下的计算结果非常接近.通过三个配合物比较来看, 在二价和三价铀配合物时, 金属富电子导致U—U周围电子密度与U—N周围差异较大, 所以计算条件(如基组、哈密顿)变化对键级结果影响显著; 而四价铀配合物中, U—U和U—N周边电子密度差异不再像低价化合物那么明显, 所以ADF和Priroda的计算结果也相对接近.另外, 从表 2可以看到, ADF计算的Gophinatan-Jug (G-J)和不同级别Nalewajski-Mrozek [N-M(i)]与其计算的Mayer键级也有差异.为进一步考察泛函的影响, 使用杂化泛函B3LYP和mPW1PW(ADF程序)计算的二价铀配合物U—U的Mayer键级分别为3.65和3.67, 比PBE计算值低很多, 但是其平均U—N键级值则相对较高.值得指出的是, 这一数值却接近Priroda的计算结果.总之, 键级的计算结果与使用的基组(Gaussian和Slater)、相对论哈密顿(AE和ZORA)、密度泛函方法(PBE、B3LYP和mPW1PW)和键级密度Partition处理方法(Mayer、G-J和N-M)有关.
表 2
各种泛函计算的双金属铀配合物基态U—U和U—N键长(D, Å)和键级
Table 2.
Calculated U—U and U—N bond distances (D, Å) and bond orders of the diuranium complexes in their ground states
Complex Functional Bond D ADF: DFT Pri: DFT Mayer G-Ja N-M(1)b N-M(2)b N-M(3)b Mayer [(UⅡ)2(L)] PBE U—U 2.332 4.80 4.13 4.94 4.54 4.67 3.89 (U—N)av. 2.433 0.39 0.62 0.70 0.81 0.70 0.51 B3LYP U—U 2.332 3.65 4.15 5.11 4.46 4.75 (U—N)av. 2.433 0.45 0.57 0.66 0.82 0.66 mPW1PW U—U 2.332 3.67 4.17 5.17 4.52 4.80 (U—N)av. 2.433 0.43 0.57 0.66 0.81 0.66 [(UⅢ)2(L)]2+ PBE U—U 2.474 3.56 3.40 4.15 3.37 3.81 3.18 (U—N)av. 2.352 0.46 0.74 0.85 0.99 0.84 0.63 [(UⅣ)2(L)]4+ PBE U—U 2.720 2.32 2.45 2.81 1.86 2.53 2.28 (U—N)av. 2.291 0.60 0.89 0.99 1.11 0.96 0.76 aGophinatan-Jug bond order analysis. b Nalewajski-Mrozek bond order analysis based on different partitionings. 表 2 各种泛函计算的双金属铀配合物基态U—U和U—N键长(D, Å)和键级
Table 2. Calculated U—U and U—N bond distances (D, Å) and bond orders of the diuranium complexes in their ground states3.2 原子电荷、电子自旋密度和轨道布居
Priroda程序计算的[(Um)2(L)]n+ (m＝Ⅱ~Ⅳ, n＝0~4) 的铀原子电荷(QU)分别为1.06~1.09、1.35~1.38和1.52~1.53(表 1).很明显, 这些数值与金属正常氧化态偏离很多, 但随着铀原子氧化态增加而增大.相比之下, 得到的铀原子电子自旋密度(SU)与其预期常规数值偏差较小. 图 2绘制出这一差值(∆SU)与电子自旋态的相关图.可以看出, 二价铀配合物所有电子自旋态的∆SU均为负值, 表明电子密度由金属流向配体; 而其他两类铀配合物的∆SU均为正值, 显示有更多电子密度定域到金属上, 且四价的电子转移大于三价; 因此, 整体呈现∆SU数值随着金属氧化态增大而增大的规律性变化.大部分铀配合物电子自旋态的∆SU小于0.1, 表明其SU能够反映其电子自旋态结构; 二价铀配合物九重态和四价铀配合物的三重态的SU分别为3.79和1.24, 与常规预期值相差最大, 对应的差值∆SU分别为0.21和0.24.
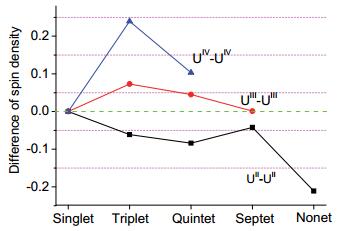图 2
计算的[(Um)2(L)]n+ (m＝Ⅱ, n＝0; m＝Ⅲ, n＝2; m＝Ⅳ, n＝4) 不同电子自旋异构体中铀自旋密度值与其期望值的差值, 即单重态、三重态、五重态、七重态和九重态的期望值分别为0、1、2、3和4
Figure 2.
Difference (∆SU) of spin density of uranium atom of [(Um)2(L)]n+ (m＝Ⅱ,
n＝0; m＝Ⅲ, n＝2; m＝Ⅳ, n＝4) in various electronic spin states from the respective expected formal value, i.e. 0, 1, 2, 3 and 4 for the singlet, triplet, quintet, septet and nonet states, respectively.
表 3列出了ADF对配合物基态铀的电荷(QU)和电子自旋密度(SU)的计算结果.就铀的电荷而言, ADF所得数值略高于Priroda计算结果, 由于铀电荷计算受基组影响很大, 所以它们之间的不同可归结为基组差异引起. ADF计算二价、三价和四价铀配合物基态的SU分别为0.96、1.11、2.13, 与Priroda计算相差不到0.04.对二价铀配合物的SU数值而言, 使用ADF的杂化泛函(B3LYP和mPW1PW)方法得到的数值与PBE方法的非常接近, 偏差不到0.02.可以看出, 电子自旋密度不但能够比电荷更好的描述配合物的电子自旋态, 而且不受基组和密度泛函的影响.
表 3
ADF程序计算的配合物基态中铀的电子自旋密度(SU)、电荷(QU)和原子布居
Table 3.
Electron-spin density (SU), charge (QU) and atomic populations of the uranium atom in the diuranium complexes in their ground states calculated by the ADF code
Complex Approach SU QU Atomic population [(UⅡ)2(L)] PBE/sol 0.955 1.070 5f3.156s1.906p6.006d1.827p0.06 PBE/gas 0.951 1.092 5f3.156s1.906p6.006d1.827p0.04 B3LYP/sol 0.931 1.044 5f2.986s2.006p5.956d1.757s0.27 mPW1PW/sol 0.936 1.067 5f2.956s2.006p5.956d1.787s0.25 [(UⅢ)2(L)]2+ PBE/sol 1.111 1.448 5f3.046s1.886p5.846d1.80 [(UⅣ)2(L)]4+ PBE/sol 2.132 1.710 5f2.986s1.976p5.706d1.64 表 3 ADF程序计算的配合物基态中铀的电子自旋密度(SU)、电荷(QU)和原子布居
Table 3. Electron-spin density (SU), charge (QU) and atomic populations of the uranium atom in the diuranium complexes in their ground states calculated by the ADF code使用ADF方法分析了不同铀氧化态配合物基态的金属原子布居. PBE方法计算的UⅡ的电子组态为5f3.156s1.906p6.006d1.827p0.06; 随着铀氧化态的增加, UⅢ的5f和6p轨道分别减少0.11和0.16个电子, 而6s和6d轨道中电子变化不大; 从三价铀到四价铀, 6s轨道电子增加0.09, 而其他轨道则减少0.06~0.16. GGA方法表明电子更容易定域于5f轨道, 且分子环境(溶液和气态)对原子布居几乎没有影响.杂化泛函方法得到不同的结果, 如二价铀配合物的计算表明杂化泛函方法相对GGA方法低估了电子在5f轨道中的分布, 其计算数值降低了0.17~0.20, 而高估了电子在6s和7s轨道中的占据, 相对增加共计0.29~0.31个电子.这一结果与密度泛函方法的本质密切相关[16, 35~37].
3.3 分子轨道和金属多重键
使用溶剂化自洽反应场模型模拟分子环境, 计算三种铀氧化态配合物的基态电子性质, 同时与三价铀配合物的五重态的进行比较. 图 3绘制α自旋轨道能级, 并标明轨道性质.它们的定量轨道成分和轨道图见支持信息表S2~S4和图S1~S3.
图 3
PBE/Scalar-ZORA/sol(THF)方法计算[(Um)2(L)]n+ (m＝Ⅱ~Ⅳ; n＝0~4) 基态的α自旋轨道能级, 并与三价配合物的五重态进行比较.为方便, 二价配合物的所有轨道整体下移2.12 eV, 三价配合物的三重态整体上移0.05 eV.而四价配合物的向上平移2.01 eV
Figure 3.
Energetic levels and character of frontier molecular orbitals (α-spin) of [(Um)2(L)]n+ (m＝Ⅱ~Ⅳ; n＝0~4) in ground states calculated by PBE/Scalar-ZORA/sol(THF), compared with those of the second lowest-state [(UⅢ)2(L)]2+ (quintet). For convenient comparison, overall orbitals of the divalent complex (first column) were down-shifted by 2.12 eV, those of the triplet state of the trivalent complex (second column) up-shifted by 0.05 eV, while those of the tetravalent complex (fourth column) up-shifted by 2.01 eV
图 3显示, 这些配合物拥有金属性质的前线分子轨道(包括高占据轨道和低非占据轨道), 配体贡献为主的占据轨道能量相对较低.有趣的是, 最高配体占据轨道与其相邻的低金属占据轨道之间能量差逐渐缩小.二价铀配合物的HOMO－LUMO轨道能级差为1.15 eV, 三价铀配合物的能量差减小至0.39 eV(三重态)和0.31 eV(五重态), 然而四价铀配合物的最高能配体轨道能量急剧升高, 并超过σ(U—U)金属轨道0.09 eV, 即其HOMO－3 (H－3) 配体轨道插入到两个金属σ成键轨道H－4和H－2之间.在以前系列配合物AnmCpn (Cp＝C5H5; An＝Th~Cm; m＝Ⅲ, n＝3; m＝Ⅳ, n＝4) 研究中[38, 39], 发现随着锕系金属原子序数增加, 最高能配体占据轨道能量逐渐接近、并在超钚元素时高过相邻最低能金属轨道能级; 得出金属和配体轨道能级匹配可以在一定程度上增大配体与金属相互作用的结论, 从而为次锕元素(如Am和Cm等)分离化学提供理论指导[40].本文研究发现, 金属铀氧化态变化同样能够调控配体和金属轨道能级匹配程度和影响其相互作用.值得指出的是, Priroad/ADF对二价、三价和四价铀配合物基态的U—N的Mayer键级计算分别为0.51/0.39、0.63/0.46和0.76/0.60, 即随着铀氧化态增加而U—N键级增大, 这一结果直接证明配体与金属的成键作用增强. U—N的G-J和N-M(i)键级给出同样的规律(表 2).
二价铀配合物具有三重态基态, 它的HOMO和H－1(α自旋)轨道为δ(U—U)成键性质, 如图 4所示, 分别具有一个成单电子, 且自旋平行.能量较低的σ和π轨道均为双占据轨道.因此, 二价铀配合物具有πy2πx2σ2δ1δ1电子组态. 表 4和图 5给出了α自旋前线轨道成分分析.很明显, 该配合物有五个高占据金属性质轨道, HOMO~H－4.它们主要为U(f)轨道成分, 并有部分U(d)轨道特征, 其中H－4中有29% U(d)贡献; H－2中还有13% U(s)和7%的U(p)参与. H－5主要为配体参与的轨道(77%).
图 4
配合物[(UⅡ)2(L)]基态的U(f)和配体性质轨道(α自旋)
Figure 4.
Characteristic U(f) and ligand-based α-spin orbitals of the ground (triplet) state of [(UⅡ)2(L)]
表 4
配合物[(UⅡ)2(L)]基态的α自旋轨道成分
Table 4.
Contributions (%) to the α-spin orbitals of the ground (triplet) state of [(UⅡ)2(L)]a
Orbital Energy/eV 2Ub Ligand s p d f L+2 －2.719 90.5 L+1 －2.720 8.7 8.9 42.3 12.3 LUMO －2.737 4.1 6.8 56.6 HOMO －3.100 2.2 79.7 H－1 －3.214 12.9 75.1 H－2 －3.604 12.9 7.0 7.2 64.2 H－3 －3.654 18.1 67.2 H－4 －3.867 29.1 48.8 H－5 －5.017 2.3 77.1 a The sum of contributions for each orbital is less than 100%, for the output of SFO contributions smaller than 1% in the calculations is suppressed. bTotal values of two uranium atoms are given here, for each uranium has approximately identical components. 表 4 配合物[(UⅡ)2(L)]基态的α自旋轨道成分
Table 4. Contributions (%) to the α-spin orbitals of the ground (triplet) state of [(UⅡ)2(L)]a
图 5
Density of states (DOS) of α-spin orbitals of the triplet state of [(UⅡ)2(L)]
Figure 5.
三重态[(UⅡ)2(L)]
α自旋轨道的态密度图
三价铀配合物基态高占据轨道(HOMO~H－3) 分别为金属铀-铀的δ、σ和π成键轨道, 具有πy2σ2πx1δ1电子组态.这些轨道仍以U(5f)成分为主, U(6d)贡献相对二价铀配合物都有所减小, 其中H－3轨道的U(6d)成分最大, 不超过13%.计算表明四价铀配合物拥有σ1σ1πx1σ1电子组态.与上面两个配合物相比, 四价配合物的轨道成分发生较大变化.如前所述, 配体轨道能量升高并超过金属轨道.这导致其占据轨道主要由U参与为主, 而配体部分参与成键.例如, H－1和H－2中分别有23%和21%的配体贡献.另外, 金属成键轨道(HOMO、H－1、H－2和H－4) 完全是U(5f)性质, 而U(6d)仅有不超过3%的贡献.
使用ADF和Multiwfn程序计算QTAIM性质参数, 电子密度ρ(r)、拉普拉斯密度∇2ρ(r)和能量密度H(r).对于二价铀配合物, 除九重态外, 所有的ρ(r)均大于0.1, 而∇2ρ(r)大于0.34, 其H(r)为负值, 说明二价U配合物的U—U键具有部分共价特征.其中, 三重基态的计算值分别为0.19、0.52和－0.11.计算表明, QTAIM参数数值(绝对值)随铀氧化态的增加而逐渐减小, 说明铀-铀金属键强度逐渐减小.结合以上U—U键长、键级、伸缩振动频率和分子轨道分析, 二价、三价和四价铀配合物分别具有U—U弱四重键、三重键和双重键性质.
表 5
双金属铀配合物中U—U键临界点电子密度参数: ρ(r)、∇2ρ(r)、H(r) (单位: au)
Table 5.
Electron density [ρ(r), au], its Laplacian [∇2ρ(r), au] and energy density [H(r), au] at U—U bond critical point in diuranium complexes, where all electronic states were calculated for the divalent uranium complex, and only the ground state for other complexes
Complex ES ρ(r) ∇2ρ(r) H(r) [(UⅡ)2(L)] nonet 0.088 0.266 －0.030 septet 0.122 0.343 －0.049 quintet 0.169 0.344 －0.067 triplet 0.189 0.517 －0.109 singlet 0.191 0.552 －0.112 [(UⅢ)2(L)]2+ triplet 0.125 0.421 — a [(UⅣ)2(L)]4+ quintet 0.082 0.251 －0.026 a Don’t obtain the value. 表 5 双金属铀配合物中U—U键临界点电子密度参数: ρ(r)、∇2ρ(r)、H(r) (单位: au)
Table 5. Electron density [ρ(r), au], its Laplacian [∇2ρ(r), au] and energy density [H(r), au] at U—U bond critical point in diuranium complexes, where all electronic states were calculated for the divalent uranium complex, and only the ground state for other complexes4 结论
使用相对论广义梯度和杂化密度泛函理论方法探索二价双金属铀配合物的各种电子自旋态结构、电子自旋密度、基态电子结构和金属多重键性质, 并与其三价和四价铀同类物进行比较.
优化得到二价铀配合物有五种电子自旋态, 其三重态为基态, 不同泛函的计算得到相同结论.三价和四价铀化合物的基态分别为三重和五重态.二价、三价和四价铀化合物的基态U—U键长分别为2.33、2.47和2.72 Å, Mayer键级为3.89、3.18和2.28, 伸缩振动频率为259、214和140 cm–1; 并分别具有πy2πx2σ2δ1δ1、πy2σ2πx1δ1和σ1σ1πx1σ1电子组态.结合QTAIM拓扑分析, 指认二价、三价和四价双铀配合物分别具有弱U—U四重键、三重键和双重键本质.
分子轨道分析表明二价铀配合物的U—U成键的高占据轨道, 主要由U(5f)贡献且混有部分U(6d)成分; 其最高能配体占据轨道与上面相邻的最低能金属轨道能量相差1.15 eV.三价铀配合物的高占据轨道成分仍以U(5f)为主, U(6d)贡献相对减小; 金属轨道与最高占据配体轨道能量差仅为0.39 eV.相比之下, 四价铀配合物的电子结构发生较大变化.首先配体轨道能量急剧升高, 并超过金属轨道0.09 eV; 其次, 配体对轨道成分贡献相对二价和三价配合物明显增大; 最后, 金属成键轨道完全为U(5f)性质, U(6d)贡献可以忽略.
目前研究发现随着锕系金属原子序数的增加, 最高配体占据轨道能量逐渐接近、并在超钚元素配合物时超越相邻最低金属轨道能级的现象, 这归结为金属和配体轨道能级匹配是它们相互作用增强的主因[38, 39].本文研究发现, 通过变化金属铀的氧化态, 同样可以实现配体和金属轨道能级匹配程度的有效调控, 并增加金属和配体的相互作用.
-
-
[1]
Hashke, J. M.; Stakebake, J. L. In The Chemistry of the Actinide and Transactinide Elements, Eds.: Morss, L. R.; Edelstein, N. M.; Fuger, J., Springer, Netherlands, 2006, p. 3199.
-
[2]
Liddle, S. T. Angew. Chem. Int. Ed. 2015, 54, 8604. doi: 10.1002/anie.201412168
-
[3]
MacDonald, M. R.; Fieser, M. E.; Bates, J. E.; Ziller, J. W.; Furche, F.; Evans, W. J. J. Am. Chem. Soc. 2013, 135, 13310. doi: 10.1021/ja406791t
-
[4]
La Pierre, H. S.; Scheurer, A.; Heinemann, F. W.; Hieringer, W.; Meyer, K. Angew. Chem. Int. Ed. 2014, 53, 7158. doi: 10.1002/anie.201402050
-
[5]
Meyer, G. Angew. Chem. Int. Ed. 2014, 53, 3550. doi: 10.1002/anie.v53.14
-
[6]
Sessler, J. L.; Cho, W. S.; Dudek, S. P.; Hicks, L.; Lynch, V. M.; Huggins, M. T. J. Porphyr. Phthalocyanines 2003, 7, 97. doi: 10.1142/S1088424603000136
-
[7]
Givaja, G.; Blake, A. J.; Wilson, C.; Schroder, M.; Love, J. B. Chem. Commun. 2003, 2508.
-
[8]
Arnold, P. L.; Patel, D.; Wilson, C.; Love, J. B. Nature 2008, 451, 315. doi: 10.1038/nature06467
-
[9]
Arnold, P. L.; Potter, N. A.; Magnani, N.; Apostolidis, C.; Griveau, J.-C.; Colineau, E.; Morgenstern, A.; Caciuffo, R.; Love, J. B. Inorg. Chem. 2010, 49, 5341. doi: 10.1021/ic100374j
-
[10]
Arnold, P. L.; Potter, N. A.; Carmichael, C. D.; Slawin, A. M. Z.; Roussel, P.; Love, J. B. Chem. Commun. 2010, 46, 1833. doi: 10.1039/b921132b
-
[11]
Arnold, P. L.; Hollis, E.; White, F. J.; Magnani, N.; Caciuffo, R.; Love, J. B. Angew. Chem. Int. Ed. 2011, 50, 887. doi: 10.1002/anie.201005511
-
[12]
Arnold, P. L.; Jones, G. M.; Odoh, S. O.; Schreckenbach, G.; Magnani, N.; Love, J. B. Nat. Chem. 2012, 4, 221. doi: 10.1038/nchem.1270
-
[13]
Zegke, M.; Nichol, G. S.; Arnold, P. L.; Love, J. B. Chem. Commun. 2015, 51, 5876. doi: 10.1039/C5CC00867K
-
[14]
Su, D.-M.; Zheng, X.-J.; Schreckenbach, G.; Pan, Q.-J. Organometallics 2015, 34, 5225. doi: 10.1021/acs.organomet.5b00649
-
[15]
Laikov, D. N.; Ustynyuk, Y. A. Russ. Chem. Bull. 2005, 54, 820. doi: 10.1007/s11172-005-0329-x
-
[16]
Perdew, J. P.; Burke, K.; Ernzerhof, M. Phys. Rev. Lett. 1996, 77, 3865. doi: 10.1103/PhysRevLett.77.3865
-
[17]
Baerends, E. J.; Ziegler, T.; Autschbach, J.; Bashford, D.; Bérces, A.; Bickelhaupt, F. M.; Bo, C.; Boerrigter, P. M.; Cavallo, L.; Chong, D. P.; Deng, L.; Dickson, R. M.; Ellis, D. E.; van Faassen, M.; Fan, L.; Fischer, T. H.; Fonseca Guerra, C.; Franchini, M.; Ghysels, A.; Giammona, A.; van Gisbergen, S. J. A.; Götz, A. W.; Groeneveld, J. A.; Gritsenko, O. V.; Grüning, M.; Gusarov, S.; Harris, F. E.; van den Hoek, P.; Jacob, C. R.; Jacobsen, H.; Jensen, L.; Kaminski, J. W.; van Kesse, G.; Kootstra, F.; Kovalenko, A.; Krykunov, M. V.; van Lenthe, E.; McCormack, D. A.; Michalak, A.; Mitoraj, M.; Morton, S. M.; Neugebauer, J.; Nicu, V. P.; Noodleman, L.; Osinga, V. P.; Patchkovskii, S.; Pavanello, M.; Philipsen, P. H. T.; Post, D.; Pye, C. C.; Ravenek, W.; Rodríguez, J. I.; Ros, P.; Schipper, P. R. T.; van Schoot, H.; Schreckenbach, G.; Seldenthuis, J. S.; Seth, M.; Snijders, J. G.; Solà, M.; Swart, M.; Swerhone, D.; te Velde, G.; Vernooijs, P.; Versluis, L.; Visscher, L.; Visser, O.; Wang, F.; Wesolowski, T. A.; van Wezenbeek, E. M.; Wiesenekker, G.; Wolff, S. K.; Woo, T. K.; Yakovlev, A. L.; ADF2014.06 ed.; SCM, Theoretical Chemistry, Vrije Universiteit: Amsterdam, The Netherlands, 2014.
-
[18]
Klamt, A.; Jonas, V.; Burger, T.; Lohrenz, J. C. W. J. Phys. Chem. A 1998, 102, 5074. doi: 10.1021/jp980017s
-
[19]
Bao, Z.; Zhao, H.-B.; Qu, N.; Schreckenbach, G.; Pan, Q.-J. Dalton Trans. 2016, 45, 15970. doi: 10.1039/C6DT01930G
-
[20]
赵思魏, 钟宇曦, 郭元茹, 张红星, 潘清江, 化学学报, 2016, 74, 683. doi: 10.3866/PKU.WHXB201512302Zhao, S.; Zhong, Y.; Guo, Y.; Zhang, H.; Pan, Q. Acta Chim. Sinica 2016, 74, 683. doi: 10.3866/PKU.WHXB201512302
-
[21]
van Lenthe, E.; Baerends, E. J.; Snijders, J. G. J. Chem. Phys. 1993, 99, 4597. doi: 10.1063/1.466059
-
[22]
Frisch, M. J.; Trucks, G. W.; Schlegel, H. B.; Scuseria, G. E.; Robb, M. A.; Cheeseman, J. R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G. A.; Nakatsuji, H.; Caricato, M.; Li, X.; Hratchian, H. P.; Izmaylov, A. F.; Bloino, J.; Zheng, G.; Sonnenberg, J. L.; Hada, M.; Ehara, M.; Toyota, K.; Fukuda, R.; Hasegawa, J.; Ishida, M.; Nakajima, T.; Honda, Y.; Kitao, O.; Nakai, H.; Vreven, T.; Montgomery, J. A., Jr.; Peralta, J. E.; Ogliaro, F.; Bearpark, M.; Heyd, J. J.; Brothers, E.; Kudin, K. N.; Staroverov, V. N.; Kobayashi, R.; Normand, J.; Raghavachari, K.; Rendell, A.; Burant, J. C.; Iyengar, S. S.; Tomasi, J.; Cossi, M.; Rega, N.; Millam, J. M.; Klene, M.; Knox, J. E.; Cross, J. B.; Bakken, V.; Adamo, C.; Jaramillo, J.; Gomperts, R.; Stratmann, R. E.; Yazyev, O.; Austin, A. J.; Cammi, R. P., C.; Ochterski, J. W.; Martin, R. L.; Morokuma, K.; Zakrzewski, V. G.; Voth, G. A.; Salvador, P.; Dannenberg, J. J.; Dapprich, S.; Daniels, A. D.; Farkas, O.; Foresman, J. B.; Ortiz, J. V.; Cioslowski, J.; Fox, D. J.; Gaussian 09, Revision D.01 ed. Gaussian, Inc., Wallingford CT, 2009.
-
[23]
Cao, X.; Dolg, M.; Stoll, H. J. Chem. Phys. 2003, 118, 487. doi: 10.1063/1.1521431
-
[24]
Lu, T.; Chen, F. J. Comput. Chem. 2012, 33, 580. doi: 10.1002/jcc.v33.5
-
[25]
Patel, D.; Liddle, S. T. Rev. Inorg. Chem. 2012, 32, 1. doi: 10.1515/revic.2012.0001
-
[26]
Patel, D.; King, D. M.; Gardner, B. M.; McMaster, J.; Lewis, W.; Blake, A. J.; Liddle, S. T. Chem. Commun. 2011, 47, 295. doi: 10.1039/C0CC01387K
-
[27]
Gardner, B. M.; Patel, D.; Cornish, A. D.; McMaster, J.; Lewis, W.; Blake, A. J.; Liddle, S. T. Chem. Eur. J. 2011, 17, 11266. doi: 10.1002/chem.201101394
-
[28]
Liddle, S. T.; McMaster, J.; Mills, D. P.; Blake, A. J.; Jones, C.; Woodul, W. D. Angew. Chem. Int. Ed. 2009, 48, 1077. doi: 10.1002/anie.v48:6
-
[29]
Hlina, J. A.; Pankhurst, J. R.; Kaltsoyannis, N.; Arnold, P. L. J. Am. Chem. Soc. 2016, 138, 3333. doi: 10.1021/jacs.5b10698
-
[30]
Cavigliasso, G.; Kaltsoyannis, N. Inorg. Chem. 2006, 45, 6828. doi: 10.1021/ic060777e
-
[31]
Cavigliasso, G.; Kaltsoyannis, N. Dalton Trans. 2006, 5476.
-
[32]
Roos, B. O.; Gagliardi, L. Inorg. Chem. 2006, 45, 803. doi: 10.1021/ic051665a
-
[33]
Zhou, J.; Sonnenberg, J. L.; Schlegel, H. B. Inorg. Chem. 2010, 49, 6545. doi: 10.1021/ic100427t
-
[34]
Long, B.; Bao, J. L.; Truhlar, D. G. J. Am. Chem. Soc. 2016, 138, 14409. doi: 10.1021/jacs.6b08655
-
[35]
熊忠华, 陈琦, 郑秀梅, 魏锡文, 化学学报, 2005, 63, 572. doi: 10.3321/j.issn:0567-7351.2005.07.004Xiong, Z.; Chen, Q.; Zheng, X.; Wei, X. Acta Chim. Sinica 2005, 63, 572. doi: 10.3321/j.issn:0567-7351.2005.07.004
-
[36]
张益伟, 马雪璐, 张欣, 雷鸣, 化学学报, 2016, 74, 340. doi: 10.11862/CJIC.2017.034Zhang, Y.; Ma, X.; Zhang, X.; Lei, M. Acta Chim. Sinica 2016, 74, 340. doi: 10.11862/CJIC.2017.034
-
[37]
杨一诺, 张琪, 石景, 傅尧, 化学学报, 2016, 74, 422. doi: 10.3866/PKU.WHXB201512082Yang, Y.; Zhang, Q.; Shi, J.; Fu, Y. Acta Chim. Sinica 2016, 74, 422. doi: 10.3866/PKU.WHXB201512082
-
[38]
Kirker, I.; Kaltsoyannis, N. Dalton Trans. 2011, 40, 124. doi: 10.1039/C0DT01018A
-
[39]
Tassell, M. J.; Kaltsoyannis, N. Dalton Trans. 2010, 39, 6719. doi: 10.1039/c000704h
-
[40]
Liu, J.-B.; Chen, G. P.; Huang, W.; Clark, D. L.; Schwarz, W. H. E.; Li, J. Dalton Trans. 2017, 46, 2542. doi: 10.1039/C6DT03953G
-
[1]
-
图 1 用Priroda程序在PBE/B-Ⅰ方法下优化的H4L配体和[(Um)2(L)]n+ (m＝Ⅱ~Ⅳ, n＝0~4) 配合物结构, 其中分别给出了配合物的侧视图(上)和正视图(下)
Figure 1 Optimized structures (left) of the ligand H4L and the complexes [(Um)2(L)]n+ (m＝Ⅱ~Ⅳ, n＝0~4) in Priroda codes where side-on (top) and face-on (bottom) views are shown
图 2 计算的[(Um)2(L)]n+ (m＝Ⅱ, n＝0; m＝Ⅲ, n＝2; m＝Ⅳ, n＝4) 不同电子自旋异构体中铀自旋密度值与其期望值的差值, 即单重态、三重态、五重态、七重态和九重态的期望值分别为0、1、2、3和4
Figure 2 Difference (∆SU) of spin density of uranium atom of [(Um)2(L)]n+ (m＝Ⅱ, n＝0; m＝Ⅲ, n＝2; m＝Ⅳ, n＝4) in various electronic spin states from the respective expected formal value, i.e. 0, 1, 2, 3 and 4 for the singlet, triplet, quintet, septet and nonet states, respectively.
图 3 PBE/Scalar-ZORA/sol(THF)方法计算[(Um)2(L)]n+ (m＝Ⅱ~Ⅳ; n＝0~4) 基态的α自旋轨道能级, 并与三价配合物的五重态进行比较.为方便, 二价配合物的所有轨道整体下移2.12 eV, 三价配合物的三重态整体上移0.05 eV.而四价配合物的向上平移2.01 eV
Figure 3 Energetic levels and character of frontier molecular orbitals (α-spin) of [(Um)2(L)]n+ (m＝Ⅱ~Ⅳ; n＝0~4) in ground states calculated by PBE/Scalar-ZORA/sol(THF), compared with those of the second lowest-state [(UⅢ)2(L)]2+ (quintet). For convenient comparison, overall orbitals of the divalent complex (first column) were down-shifted by 2.12 eV, those of the triplet state of the trivalent complex (second column) up-shifted by 0.05 eV, while those of the tetravalent complex (fourth column) up-shifted by 2.01 eV
图 4 配合物[(UⅡ)2(L)]基态的U(f)和配体性质轨道(α自旋)
Figure 4 Characteristic U(f) and ligand-based α-spin orbitals of the ground (triplet) state of [(UⅡ)2(L)]
图 5 Density of states (DOS) of α-spin orbitals of the triplet state of [(UⅡ)2(L)]
Figure 5 三重态[(UⅡ)2(L)] α自旋轨道的态密度图
表 1 计算配合物在不同电子自旋态(ESS)下U—U的键长(D, Å)、键级(BO)、伸缩振动频率(ν, cm–1)和铀原子电子自旋密度(SU), 以及它们的相对能量(kJ/mol)a
Table 1. Calculated U—U distances (D, Å), bond orders (BO), stretching vibrational frequencies (ν, cm–1) and electron-spin density (SU) of uranium atoms for diuranium complexes in various electron-spin states (ESS), together with the relative energies (kJ/mol)a
Complex ESS D ν BO SU QU ΔE ΔE0 [(UⅡ)2(L)] nonet 2.668 180 2.95 3.789 1.055 68.0 64.9 septet 2.517 196 3.52 2.958 1.078 42.5 40.1 quintet 2.412 235 3.76 1.916 1.087 27.7 25.8 triplet 2.332 259 3.89 0.939 1.067 0.0 0.0 singlet 2.324 263 3.90 0.000 1.069 24.4 23.9 [(UⅢ)2(L)]2+ septet 2.622 188 3.08 3.001 1.372 26.9 26.9 quintet 2.506 201 3.14 2.045 1.373 2.8 2.3 triplet 2.474 214 3.18 1.073 1.380 0.0 0.0 singlet 2.426 220 3.17 0.000 1.349 11.9 12.3 [(UⅣ)2(L)]4+ quintet 2.720 140 2.28 2.103 1.541 0.0 0.0 triplet 2.641 149 2.33 1.240 1.516 11.8 11.8 singlet 2.627 156 2.31 0.000 1.528 31.8 31.8 a ΔE denotes the total energy and ΔE0 includes the zero-point vibration energy, which were obtained by subtracting the respective ground-state energy. Trivalent complexes were reported in our previous work[14]. 
下载: 导出CSV
表 2 各种泛函计算的双金属铀配合物基态U—U和U—N键长(D, Å)和键级
Table 2. Calculated U—U and U—N bond distances (D, Å) and bond orders of the diuranium complexes in their ground states
Complex Functional Bond D ADF: DFT Pri: DFT Mayer G-Ja N-M(1)b N-M(2)b N-M(3)b Mayer [(UⅡ)2(L)] PBE U—U 2.332 4.80 4.13 4.94 4.54 4.67 3.89 (U—N)av. 2.433 0.39 0.62 0.70 0.81 0.70 0.51 B3LYP U—U 2.332 3.65 4.15 5.11 4.46 4.75 (U—N)av. 2.433 0.45 0.57 0.66 0.82 0.66 mPW1PW U—U 2.332 3.67 4.17 5.17 4.52 4.80 (U—N)av. 2.433 0.43 0.57 0.66 0.81 0.66 [(UⅢ)2(L)]2+ PBE U—U 2.474 3.56 3.40 4.15 3.37 3.81 3.18 (U—N)av. 2.352 0.46 0.74 0.85 0.99 0.84 0.63 [(UⅣ)2(L)]4+ PBE U—U 2.720 2.32 2.45 2.81 1.86 2.53 2.28 (U—N)av. 2.291 0.60 0.89 0.99 1.11 0.96 0.76 aGophinatan-Jug bond order analysis. b Nalewajski-Mrozek bond order analysis based on different partitionings.
下载: 导出CSV
表 3 ADF程序计算的配合物基态中铀的电子自旋密度(SU)、电荷(QU)和原子布居
Table 3. Electron-spin density (SU), charge (QU) and atomic populations of the uranium atom in the diuranium complexes in their ground states calculated by the ADF code
Complex Approach SU QU Atomic population [(UⅡ)2(L)] PBE/sol 0.955 1.070 5f3.156s1.906p6.006d1.827p0.06 PBE/gas 0.951 1.092 5f3.156s1.906p6.006d1.827p0.04 B3LYP/sol 0.931 1.044 5f2.986s2.006p5.956d1.757s0.27 mPW1PW/sol 0.936 1.067 5f2.956s2.006p5.956d1.787s0.25 [(UⅢ)2(L)]2+ PBE/sol 1.111 1.448 5f3.046s1.886p5.846d1.80 [(UⅣ)2(L)]4+ PBE/sol 2.132 1.710 5f2.986s1.976p5.706d1.64
下载: 导出CSV
表 4 配合物[(UⅡ)2(L)]基态的α自旋轨道成分
Table 4. Contributions (%) to the α-spin orbitals of the ground (triplet) state of [(UⅡ)2(L)]a
Orbital Energy/eV 2Ub Ligand s p d f L+2 －2.719 90.5 L+1 －2.720 8.7 8.9 42.3 12.3 LUMO －2.737 4.1 6.8 56.6 HOMO －3.100 2.2 79.7 H－1 －3.214 12.9 75.1 H－2 －3.604 12.9 7.0 7.2 64.2 H－3 －3.654 18.1 67.2 H－4 －3.867 29.1 48.8 H－5 －5.017 2.3 77.1 a The sum of contributions for each orbital is less than 100%, for the output of SFO contributions smaller than 1% in the calculations is suppressed. bTotal values of two uranium atoms are given here, for each uranium has approximately identical components.
下载: 导出CSV
表 5 双金属铀配合物中U—U键临界点电子密度参数: ρ(r)、∇2ρ(r)、H(r) (单位: au)
Table 5. Electron density [ρ(r), au], its Laplacian [∇2ρ(r), au] and energy density [H(r), au] at U—U bond critical point in diuranium complexes, where all electronic states were calculated for the divalent uranium complex, and only the ground state for other complexes
Complex ES ρ(r) ∇2ρ(r) H(r) [(UⅡ)2(L)] nonet 0.088 0.266 －0.030 septet 0.122 0.343 －0.049 quintet 0.169 0.344 －0.067 triplet 0.189 0.517 －0.109 singlet 0.191 0.552 －0.112 [(UⅢ)2(L)]2+ triplet 0.125 0.421 — a [(UⅣ)2(L)]4+ quintet 0.082 0.251 －0.026 a Don’t obtain the value.
下载: 导出CSV
-
扫一扫看文章
计量
- PDF下载量: 7
- 文章访问数: 1250
- HTML全文浏览量: 161
下载:
